Понятие процессов системы
Процессы системы — это совокупность последовательных изменений состояния системы для достижения цели. К процессам системы относятся: § входной процесс; § выходной процесс; § переходный процесс системы. Входной процесс — множество входных воздействий, которые изменяются с течением времени. Входной процесс можно задать, если каждому моменту времени t поставить в соответствие по определенному правилу со входные воздействия х с X. Моменты времени t определены на множестве Т, t ÎТ. В результате этот входной процесс будет представлять собой функцию времени Функции входных процессов — задание по определенному правилу, в определенные моменты времени управляющих воздействий. Выходной процесс - множество выходных воздействий на окружающую среду, которые изменяются с течением времени. Воздействие системы на окружающую среду определяется выходными величинами (реакциями). Выходные величины изменяются с течением времени, образуя выходной процесс, представляющий функцию у: Т ® Y[X]. Функции выходных процессов — задание по определенному правилу, в определенные моменты времени выходных величин (реакций) системы. Множество допустимых функций, характеризующих выходной процесс, обозначим Г = {y, T ® Y}. Для обозначения мгновенных значений выходных величин в моменты t можно использовать обозначения y(t) [х]. Изменение с течением времени состояния системы вызывает движение системы, которое можно задать, если каждому моменту времени t Множество допустимых входных процессов, определяемых различными функциями на интервале [t0, t], описывается следующим образом:
Следовательно, состояние Z(t) системы в момент времени t будет зависеть от начального момента t0 Таким образом, состояние Z(t) может быть определено с помощью переходной функции состояния:
Графически переходная функция представлена на рис. 1.3.
На рис. 1.3 отрезок движения системы Переходная функция состояния должна удовлетворять следующим требованиям. Во-первых, поскольку знание начального движения системы ф0 на отрезке [t0 -
Z(t) =
должно быть определено во всех t ³ t0 — Во-вторых, переходная функция состояния должна быть согласована с начальным движением и начальным состоянием
Z(t) = Z(to) =
для всех t В-третьих, один и тот же входной процесс со определяет состояние системы на конце интервала времени (t0, t] независимо от того, действовал ли он последовательно, сначала на интервале (t0, t], а затем на интервале (t', t], или на всем интервале (t0, t]. Переходная функция состояния описывает переходный процесс системы. Переходный процесс системы (процесс системы) — множество преобразований начального состояния и входных воздействий в выходные величины, которые изменяются с течением времени по определенным правилам.
|

 : Т® Y [х].
: Т® Y [х]. Т по определенному правилу
Т по определенному правилу  поставить в соответствие состояние z
поставить в соответствие состояние z  ®-Z}, где
®-Z}, где  } множество возможных величин отрезков
} множество возможных величин отрезков 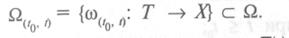
 Т, текущего времени t
Т, текущего времени t  (t0,t) на интервале (t0,t)
(t0,t) на интервале (t0,t)

 (t0,t)
(t0,t)  — отрезка переходной функции на интервале (t0, t].
— отрезка переходной функции на интервале (t0, t].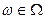 ,. Эти условия устанавливают также независимость начального движения
,. Эти условия устанавливают также независимость начального движения 


