Фактора j
После получения обобщенной матрицы предпочтений Р, элементы которой рij представляют относительное число предпочтений, полученных от всех экспертов, по каждому фактору перед каждым другим фактором, производится их шкалирование. Шкалирование может быть основано на законе сравнительных суждений, впервые сформулированном Л. Терстоуном. Суть этого подхода состоит в следующем. Если парное сравнение факторов выполняется относительно большим числом экспертов (т ³ 25), то полученные разности между их оценками обладают нормальным распределением. Пусть т экспертов приписывают п признакам Ri (i1, i2,..., in) числа Sj (j1 j2,…, jn), в соответствии со степенью обладания ими каким-то качеством X. Тогда числа Sj представляют собой шкальные оценки Ri, а разность между такими оценками двух объектов Ri и Rj (если оценки не коррелируют между собой) можно выразить с помощью модели шкалы
Si - Sj = Zijsij, (7.9)
где Si, Sj — шкальные оценки факторов; sij — среднее квадратическое (стандартное) отклонение предполагаемого распределения различий между Si и Sj, Zij — нормированное отклонение, соответствующее рij, представляющему долю случаев предпочтения фактора i фактору j, т.е.
Взаимоотношение между Z ij и рij иллюстрирует рис. 7.3, где заштрихованная площадь под кривой показывает относительное число предпочтений фактора i фактору j, когда Z ij измеряется в единицах стандартного отклонения.
Для упрощения можно принять, что s ij в формуле (7.9)равно единице, тогда Si – Sj = Z ij
При этом допускается, что площадь под кривой нормированного нормального распределения от - 3s до +3s равна единице. В действительности реальные оценки отличаются от ожидаемого ряда Z ij. Поэтому задача заключается в нахождении множества оценок, для которых это расхождение будет минимальным. Таким образом, процедура построения шкальных оценок состоит в том, чтобы обратить наблюдаемые отношения рij (матрица Р) в ожидаемые Z ij по уравнению (7.11), используя таблицу нормированного нормального распределения. Эти Z ij составляют матрицу с двумя входами или матрицу основного преобразования Z, с рядами цифр для каждого фактора i и столбцами цифр для каждого фактора j, как это показано в табл. 7.10. В матрице Z каждая оценка z ij — это различие между параметром i и параметром j в стандартных отклонениях, причем сумма этих оценок Zi = Szi, а среднее значение
Таблица 7.10. Матрица Z: основное преобразование (различия)
При этом рij рассматривается как площадь нормированного нормального распределения от - ¥ до Z Значения функции такого распределения приведены во многих книгах по статистике. Заметим, что z ij логически равно нулю и что z ij = - z ij. Если любое z ij оказывается большим, чем +2,0, или же меньшим, чем —2,0, оно отвергается как нестабильное. Если ни одна из оценок z ij не будет отвергнута на основании этого правила, то шкальная оценка фактора i будет равна средней величине всех оценок в i-м столбце данной матрицы. Когда некоторое z ij отвергается, то в таблице ставится прочерк. Для каждой пары последовательных столбцов данных необходимо рассчитать разность оценок и поместить ее в отдельную матрицу различий. При этом разница между двумя прочерками или между значением и прочерком считается несущественной, и в матрице различий ставится прочерк. Таким образом, произвольно установив S1 = 0, можно определить остальные шкальные оценки. Очевидно, что метод парных сравнений является интервальным, поскольку не только шкальный фактор, но и нулевая точка шкалы устанавливаются здесь произвольно. При большом числе факторов может быть использован другой интервальный метод, называемый методом последовательных интервалов. Здесь принимается, что границы интервалов могут быть установлены так, чтобы все распределения суждений о факторе были нормальными (см. [7.1]). Представим, что интервалы проранжированы в порядке от наименее до наиболее предпочтительного. Пусть pjg — относительное число экспертов, которые поместили фактор j в интервале g или в любом другом интервале меньшего рангового порядка. Пусть Zjg будет нормированным нормальным отклонением, соответствующим pjg. Тогда
где t - граница между интервалами g и g + 1; Sj — шкальная оценка фактора j; sj — стандартное отклонение фактора j. Принимая sj = 1, получим
На рис. 7.4 показано распределение двух признаков с различным стандартным отклонением.
Для получения шкальных оценок S и границ интервалов tg, эксперты должны расположить т факторов в М интервалах (М < т). Тогда относительное число экспертов, которые поместили фактор j в интервале g или в любом другом интервале меньшего ранга, pjg = я,.. /N. Затем по таблице нормированного нормального распределения в соответствии с формулой (7.12) для каждого pjg определяется Zjg. Для получения шкальных оценок и границ интервалов можно использовать и метод обращения полученных из наблюдений величин pjg в Z.g, применяемый при парном сравнении. Приняв ti = 0, вычисляют с помощью подобных таблиц границы интервалов, а затем конструируется четвертая матрица, значения оценок которой находятся путем вычитания каждой записи g-ro ряда матрицы Zig из полученной оценки tg. Средняя величина ряда в этой матрице — это шкальная оценка соответствующего признака.
|

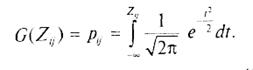

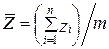 ,, где т — число экспертов.
,, где т — число экспертов.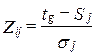 ,
, (7.13)
(7.13)



