Метод анализа иерархий

 

¨ сущность и содержание анализа иерархий

¨ пример применения метода анализа иерархий

 

Сущность и содержание анализа иерархий

 

Метод анализа иерархий (МАИ) является системной процедурой для иерархического представления элементов, определяющих суть любой проблемы.

Метод состоит в декомпозиции проблемы на все более простые составляющие части и дальнейшей обработке последовательности суждений лица, принимающего решение (ЛПР), по парным сравнениям.

В результате может быть выражена относительная степень (интенсивность) взаимодействия элементов в иерархии. Эти суждения затем выражаются численно.

Метод анализа иерархии включает процедуры синтеза множественных суждений, получения приоритетности факторов (критериев, характеристик, свойств и др.) и нахождения альтернативных решений. Полученные таким образом значения являются оценками в шкале отношений и соответствуют так называемым жестким оценкам.

Решение проблемы есть процесс поэтапного установления приоритетов и включает:

• определение и выделение проблемы (что вы хотите знать?);

• декомпозицию проблемы в иерархию;

• построение матриц парных сравнений;

• вычисление приоритетов, наибольшего собственного значения матриц суждений, индекса согласованности и отношения согласованности;

• вычисление глобальных приоритетов.

 

Определение и выделение проблемы

 

Результат оценки альтернативы, а следовательно, принятия решения, сильно зависит от начального этапа определения цели проблемы, выделения ее из среды. При определении и выделении проблемы необходимо руководствоваться следующими принципами:

¨ изучить состояние данной проблемы;

¨ определить общую цель — какую задачу вы стараетесь решить? Цели должны отражать предположения относительно причины возникновения проблемы в системе, а не просто ее проявление (например, низкий уровень морали служащих - причина низкой производительности. Низкая производительность не проблема, а ее проявление);

¨ выделить проблему из среды, установить внутренние и внешние факторы, которые влияют на решение проблемы;

¨ определить альтернативы решения проблемы;

¨ установить, на кого будет влиять ваше определение проблемы;

¨ выяснить, как определяют проблему те, на кого будет влиять определение проблемы, — можете ли вы предоставить им возможность участвовать в построении иерархии?

¨ определите, нет ли других определений проблемы, более жизнеспособных, чем ваше;

¨ рассмотрите выделенную проблему как часть нескольких проблем любой общей цели.

 

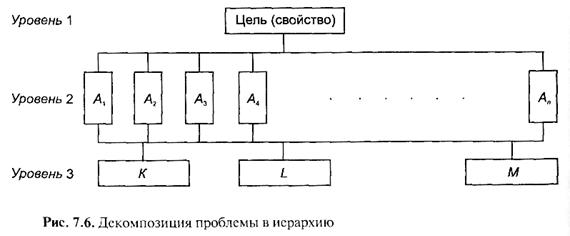
Декомпозиция проблемы в иерархию

 

Иерархия возникает, когда системы, которые функционируют как целое на одном уровне, функционируют как части системы более высокого уровня, становясь подсистемами этой системы.

Иерархия считается полной, если каждый элемент заданного уровня функционирует как фактор (критерий) для всех элементов нижестоящего уровня (рис. 7.6).

 

 

После определения (выделения) проблемы ее декомпозируют в иерархию.

Для этого:

¨ разрабатывают структуру проблемы и усовершенствуют ее, чтобы "приспособить" к проблеме;

¨ проводят "мозговой штурм" (экспертную оценку) любого возможного аспекта проблемы. Здесь определяют перечень всех факторов (критериев), располагая их в положительном или отрицательном направлении, в виде иерархии, группируя факторы в сравнимых классах;

¨ обосновывают важность каждого элемента уровня относительно примыкающего сверху уровня;

¨ для каждого уровня формулируют письменные вопросы, на которые надо ответить.

На практике встречаются два общих типа доминантных иерархий проблем [7.10].

1. Иерархия прямого процесса. Она проецирует существующее состояние проблемы на наиболее вероятное или логическое будущее (или на следствие).

2. Иерархия обратного процесса. Она определяет средства достижения
цели, чтобы помочь достижению желаемого будущего (или следствия).

 

Построение матриц парных сравнений

 

После иерархического воспроизведения проблемы возникает вопрос: как установить приоритеты факторов (критериев) и оценить каждую из альтернатив по факторам (критериям), выявив самую важную их них.

В МАИ факторы (критерии, элементы) сравниваются попарно по отношению к их воздействию ("весу" или "интенсивности") на общую для них характеристику.

Результаты парных сравнений представляются в виде квадратной матрицы. Квадратная матрица имеет равное число строк и столбцов и представляется в виде

Очевидно, что эта матрица имеет свойства обратной симметричности, т.е.

а_ij =1/a_ij,

где индексы i и j относятся к строке и столбцу соответственно.

Квадратная матрица имеет также такие характеристики, как собственные векторы и собственные значения.

Раскроем сущность парных сравнений. Пусть А₁, А₂, А₃,..., А_п — множество из п элементов матрицы и w ₁, w ₂, w ₃,..., w _п — соответственно их веса, или интенсивности.

С использованием МАИ сравним вес, или интенсивность, каждого элемента с весом, или интенсивностью, любого другого элемента множества по отношению к общему для них свойству или цели. Сравнение весов можно представить следующим образом.

Для проведения субъективных парных сравнений разработана шкала, описанная в табл. 7.16.

Таблица 7.16.