Расчет на прочность при сложном сопротивлении
Из анализа построенных эпюр внутренних силовых факторов (N и Условие прочности при растяжении-сжатии с плоским изгибом имеет вид:
где
где
А – площадь поперечного сечения детали; Wx – осевой момент сопротивления сечения детали;
Тогда окончательно условие прочности примет вид:
где знак «+» или «-» перед вторым слагаемым в левой части неравенства берется таким же, как и знак первого слагаемого (если первое слагаемое отрицательно, то берется знак «-», в противном случае – знак «+»). Принимаем форму сечения шатуна – квадрат, а материал, из которого сделан шатун – сталь 3. Определим прочные размеры сечения шатуна в данном положении и при данных нагрузках. Для стали 3 предел текучести Для квадратного сечения Подставив значения
Полученное неравенство будем решать приближенно, для этого: 1) пренебрегаем сначала первым слагаемым в левой части неравенства и находим размеры сечения:
Принимаем 2) проверяем соблюдение неравенства при найденных размерах сечения шатуна:
Так как условие выполняется, то считаем, что расчет завершен.
|

 ) следует, что опасным сечением является сечение на границе 1 и 2 силовых участков (слева), где
) следует, что опасным сечением является сечение на границе 1 и 2 силовых участков (слева), где  =-1145,07 [Н] и
=-1145,07 [Н] и  = 21,37 [Н·м]. Влиянием поперечных сил (Q) при расчете на прочность пренебрегаем в виду малости касательных напряжений.
= 21,37 [Н·м]. Влиянием поперечных сил (Q) при расчете на прочность пренебрегаем в виду малости касательных напряжений. ,
, – максимальное напряжение, возникающее в сечении детали и равное:
– максимальное напряжение, возникающее в сечении детали и равное: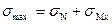 ,
, – нормальное напряжение в опасном сечении, возникающее от действия продольной силы;
– нормальное напряжение в опасном сечении, возникающее от действия продольной силы; – нормальное напряжение в опасном сечении, возникающее от действия изгибающего момента.
– нормальное напряжение в опасном сечении, возникающее от действия изгибающего момента. – допускаемое нормальное напряжение.
– допускаемое нормальное напряжение. ,
, =240 МПа, коэффициент запаса прочности принимаем n =2.
=240 МПа, коэффициент запаса прочности принимаем n =2. и
и  .
. .
. =>
=>  м.
м. м.
м. ,
, .
.


