Лінійна множинна регресія

Процедури регресійного аналізу об’єднано в модулі Multiple Regression – Множинна регресія. Як приклад, розглянемо модель залежності виходу цукру з 1 т сировини в кг (у) від цукристості буряка (х1), втрат сировини при транспортуванні й зберіганні (х2) та втрат цукру при переробці сировини (х3). Вихідні дані для аналізу наведені у табл. 5.

 

Таблиця 5

Вихідні дані для аналізу

	x1	x2	x3	y
	15,1	0,99	2,5	9,78
	15,41	1,06	2,68	9,13
	15,22	0,98	2,19	10,46
	15,16	0,95	2,06	10,69
	15,43		2,05	10,58
	15,41		2,06	10,84
	15,15	0,97	2,34	10,87
	16,06	0,9	2,24	12,24
	15,95	0,92	2,27	11,94
	15,59	0,95	2,13	11,26
	15,52	0,93	2,26	11,01
	15,33	0,97		11,88
	15,48	0,91	2,2	11,53
	15,18	0,98	2,23	11,03
	15,17	0,98	2,18	10,37

 

Запустимо програму Statistica і сформуємо файл даних. На панелі інструментів (або в меню Statistics) вибираємо модуль Multiple Regression. У стартовому вікні модуля, натиснувши кнопку Variables, вибираємо залежну (Dependent var.) і незалежну (Independent var.) змінні. На закладці Advanced можна задати додаткові параметри побудови регресійної моделі. За командою виконання програми з'явиться вікно результатів аналізу (рис. 7).

Рис. 7. Вікно Результатів множинної регресії

 

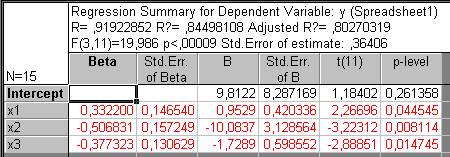
В інформаційній частині вікна міститься наступна інформація: назва залежної змінної та обсяг сукупності; наводяться значення коефіцієнтів щільності зв’язку (множинної кореляції, множинної детермінації та скоректований коефіцієнт множинної детермінації); значення F-критерію, стандартної похибки оцінювання (Standard error o f estimate), вільного члена рівняння регресії b0 (Intercept) та його похибки (Std. Error), значення критерію Стьюдента, значення bі-коефіцієнтів.

У функціональній частині вікна містяться кнопки та опції, що дозволяють усебічно розглянути результати регресійного аналізу. Так, на закладці Quik є кнопка Summary: Regression Results – Результати регресії, яка виводить таблицю результатів побудови регресії (рис. 8). У цій таблиці наведені наступні результати побудови регресії: bі-коефіцієнти (Beta) і коефіцієнти регресії bi з стандартними похибками, значення t-критерію та фактичні рівні істотності p-level. Зверніть увагу на те, що деякі рядки виділені червоним кольором. Це своєрідна підказка щодо значущості відповідних параметрів побудованої моделі. Значущість параметрів оцінюється за t-критерієм, значення якого наведені у цій же таблиці.

 

Рис. 8. Результати регресії

 

Наступним кроком є аналіз адекватності побудованої моделі. Про адекватність моделі можна судити за значеннями коефіцієнтів множинної кореляції та детермінації, за значеннями критеріїв Стьюдента та Фішера. Окрім того, слід провести аналіз залишків моделі. Для цього призначена кнопка Perform residual analysis, яка знаходиться на закладці Residuals/assumptions/prediction у вікні Результатів множинної регресії. Натиснувши цю кнопку, переходимо у вікно Аналіз залишків (рис. 9).

 

Рис. 9. Вікно налізу залишків

У цьому вікні представлений великий набір аналітичних та графічних інструментів, призначених для аналізу залишків моделі. Наглядними і найважливішими є гістограма розподілу залишків (закладка Residuals, кнопка Histogram of residuals) і графік залишків на нормальному ймовірнісному папері (закладна Probability plots, кнопка Normal plot of residuals). Відповідні графіки наведено на рис. 10, 11.

 

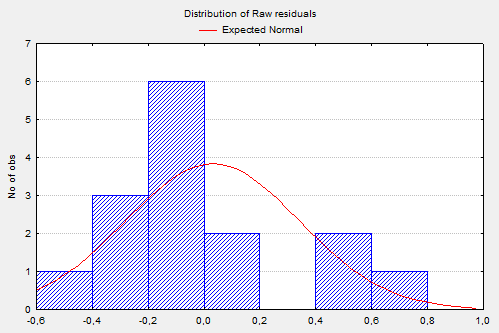
Рис. 10. Гістограма розподілу залишків

 

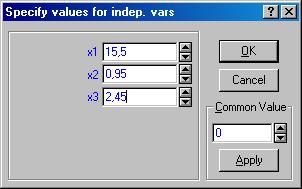
Рис. 11. Графік залишків на нормальному ймовірнісному папері

Якщо залишки розподілені за нормальним законом розподілу (гістограма залишків) і добре лягають на пряму (графік залишків на нормальному ймовірнісному папері), то це свідчить про адекватність побудованої моделі.

У модулі Множинної регресії можна знайти прогнозне значення залежної змінної. Для цього у вікні результатів необхідно перейти на закладку Residuals/assumptions/prediction і натиснути кнопку Predict dependent variable – Прогнозне значення залежної змінної. У вікні, що з’явилося, потрібно задати значення незалежних змінних, при яких слід знайти прогнозне значення залежної змінної. Наприклад, задамо такі значення (рис. 12).

 

Рис. 12. Значення незалежних змінних для обчислення прогнозного значення залежної змінної

 

Після виконання команди, отримаємо наступну таблицю результатів (рис. 13).

 

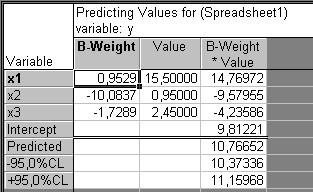
Рис. 13. Результати прогнозування

 

У цій таблиці в стовпці B-Weight указані коефіцієнти регресії при залежних змінних, у стовпці Value – значення незалежних змінних, які щойно були задані. У рядку Intercept вказане значення вільного члена регресії, у рядку Predicted – прогнозне значення залежної змінної. Нижче вказані нижня та верхня межі довірчого інтервалу. Отже, при цукристості буряка 15,5, втратах сировини при транспортуванні та зберіганні 0,95 та втратах цукру при переробці сировини 2,45, вихід цукру становитиме 10,76 кг.

Завдання. Самостійно ознайомтеся з іншими аналітичними та графічними можливостями модуля Множинної регресії. Побудуйте регресію, використовуючи інші методи (метод підключень та метод виключень). Порівняйте та проаналізуйте результати, отримані різними методами.