Аналіз особливостей задачі
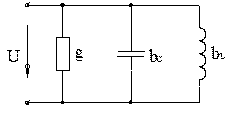
4.3.1 В якому колі може виникнути резонанс струмів і який режим називається резонансом струмів? 4.3.2 Чому дорівнює коефіцієнт потужності кола при резонансі? 4.3.3 Чому резонанс в паралельному контурі називається резонансом струмів? 4.3.4 Який характер (індуктивний чи ємнісний) має повний опір кола при частотах, нижче резонансної? 4.3.5 Чому в режимі резонансу струмів значення струму в нерозгалуженій ділянці кола найменше? 4.3.6 Як практично виявити в колі режим резонансу струмів? 4.3.7 Параметри схеми, зображеної на рис. 4.8, при частоті f становлять: g = 0,3 См, bC = 1,2 См, bL = 0,5 См. Обчислити повну провідність коли при частоті, зменшеній в два рази. 1. 1,62 См. 2. 0,5 См. 3. 2,7 См 4. 1 См 5. 2 См.
Рисунок 4.8 Рисунок 4.9
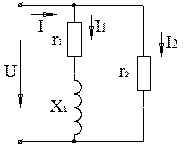
4.3.8 Обчислити коефіцієнт потужності споживача, зображеного на схемі (рис. 4.8), якщо g = 6 См, bC = 10 См, bL = 2 См. 1. cos φ = 0,445; φ > 0. 2. cos φ = 0,8; φ < 0. 3. cos φ = 0,8; φ > 0. 4. cos φ = 0,6; φ > 0. 5. cos φ = 0,6; φ < 0. 4.3.9 Для кола, зображеного на схемі (рис. 4.9), обчислити струм І, якщо І1 = 20 А, І2 = 10 1. 34 А. 2. 5 А. 3. 24,5 А. 4. 31,6 А. 5. Обчислити неможливо 4.3.10 Для кола, зображеного на схемі (рис. 4.9), обчислити струм І, якщо І1 = 10 А, І2 = 10 А, 1. 20 А. 2. 17,3 А. 3. 19,4 А. 4. 14,1 А. 5. Обчислити неможливо 4.3.11 Для схеми, зображеної на рис. 4.10, обчислити комплексне діюче значення струму, якщо 1. 16,35 4. 5
Рисунок 4.10 Рисунок 4.11
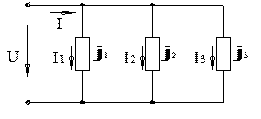
4.3.12 Для схеми, зображеної на рис. 4.11, обчислити повну провідність якщо r = 6 Ом, xC = 8 Ом, xL = 10 ом. 1. 5,84 См. 2. 0,19 См. 3. 0,0632 См. 4. 0,168 См. 5. 24 См. 4.3.13 У колі, зображеному на схемі (рис. 4.12), має місце резонанс струмів. Визначити струм ІЗ, якщо І1 = 10 А, І2 = 20 А, φ2 = 37º, φ3 = –30º. 1. 30 А. 2. –30 А. 3. 40 А. 4. 44 А. 5. 23 А.
Рисунок 4.12 Рисунок 4.13
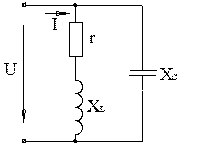
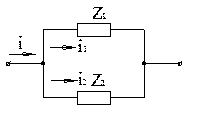
4.3.14 У колі синусоїдного струму, зображеному на схемі (рис. 4.12), має місце резонанс струмів. Визначити початковий фазовий кут φ3 струму І3, якщо І1 = 10 А, φ1 = 53º, І2 = 20 А, φ2 = 37º, І3 = 40 А. 1. –53º. 2. –90º. 3. 30º. 4. –30º. 5. 60º. 4.3.15 У колі синусоїдного, зображеному на схемі (рис. 4.12), має місце резонанс струмів. Обчислити струм І, якщо І1 = 10 А, φ1 = 53º, І2 = 20 А, φ2 = 37º, φ3 = –30º. 1. 30 А. 2. 40 А. 3. 22 А. 4. 20 А. 5. 56,6 А. 4.3.16 Для кола, зображеного на схемі (рис. 4.13), обчислити xC для випадку резонансу струмів, якщо xL = 8 Ом, r = 6 Ом. 1. 12,5 Ом. 2. 8 Ом. 3. 10 Ом. 4. 14 Ом. 5. 6 Ом. 4.3.17 У колі, зображеному на схемі (рис. 4.13), обчислити опір r для випадку резонансу струмів, якщо xC = 12,5 Ом, xL = 8 Ом. 1. 4,5 Ом. 2. 9,7 Ом. 3. 6 Ом. 4. 12,5 Ом. 5. 0. 4.3.18 Вказати вираз для визначення миттєвого значення загального струму і в схемі (рис. 4.14), якщо 1.
Рисунок 4.14
4.3.19 Для кола, зображеного на схемі (рис. 4.13), обчислити xL для випадку резонансу струмів, якщо xC =12,5 Ом, r = 6 Ом. 1. 12,5 Ом. 2. 8 Ом. 3. 6 Ом. 4. –12,5 Ом. 5. 6,5 Ом. 4.3.20 Визначити комплексні амплітуди струмів в схемі (рис. 4.14). 1. 2. 3. 4. 5. Аналіз особливостей задачі 1. Реалізуємо ручний ввід елементів масиву, якщо їх кількість не перевищує 10, в протилежному випадку будемо їх генерувати. Приймемо N = 100, оскільки потрібно обчислити добуток. Якби потрібно було обчислити суму, то значення N можна було б взяти і побільше, наприклад, N = 1000. 2. У нашій задачі доволі «цікавий» алгоритм обчислення добутку елементів з КІНЦЯ масиву. 3. У нашій задачі (з точки зору Асемблера) має сенс зробити результат (добуток позитивних елементів масиву) типу unsigned int, щоб трохи розширити діапазон результату. Зробити тип результату long int було б краще, але ми поки що не вміємо перемножувати дані <long int> * <int>. У вашого варіанту, цілком ймовірно, будуть інші, свої, СПЕЦИФІЧНІ особливості, відмінні від тих, які ми розглядаємо. Вчіться ці особливості БАЧИТИ! А для цього – розв’язуйте більше прикладів, набирайтеся досвіду... Іншого шляху немає!
|

 А, r1 = x1.
А, r1 = x1.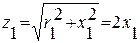 .
. В, g = 0,03 См, bL = 0,06 См, bC = 0,1 См.
В, g = 0,03 См, bL = 0,06 См, bC = 0,1 См.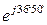 А. 2. 2000
А. 2. 2000  А.
А. А.
А.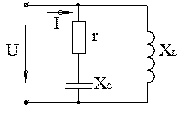

 А;
А;  А
А 2.
2.  3.
3. 
 4.
4. 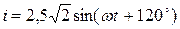 5.
5. 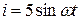
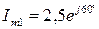 А;
А; 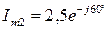 А;
А; 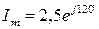 A.
A. А.
А.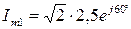 А;
А;  А;
А; 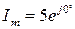 А.
А.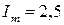 А.
А. А;
А;  А;
А;  А.
А.


