Лабораторна робота
Ітераційний метод Зейделя – це деяка модифікація методу простої ітерації. Як і метод простої ітерації, метод Зейделя передбачає розв’язання кожного рівняння окремо відносно тільки однієї змінної. Однак під час обчислення і-ї компоненти вектора розв’язку
Для реалізації методу Зейделя необхідно менше оперативної пам’яті ніж для реалізації методу простої ітерації, тому що після обчислення і-ї компоненти вектора розв’язку Приклад 2. Методом Зейделя розв’язати систему лінійних рівнянь наведену в прикладі 1, виконавши 9 ітерацій. Програма, яка реалізовує метод Зейделя, наведена на лістингу 3. На лістингу 4 наведено результати, одержані за допомогою даної програми. Для порівняння на цьому ж лістингу наведено результати, одержані за допомогою вбудованої процедури lsolve(A,b). Лістинг 3. Програма реалізації методу Зейделя
Лістинг 4. Результати роботи програми
ІНДИВІДУАЛЬНІ ЗАВДАННЯ Завдання 1. Знайти наближений розв’язок системи лінійних алгебраїчних рівнянь методом простої ітерації та методом Зейделя. Порівняти результати за точністю та кількістю ітерацій. Варіанти індивідуальних завдань: 1. 3. 5. 7. 9. 11. 13. 15. 17. 19. ЛІТЕРАТУРА 1. Фельдман Л.П., Петренко А.І., Дмитрієва О.А. Чисельні методи в інформатиці. К.: Видавнича група BHV, 2006. – 480 с. 2. Алексеев Е.П., Чесноков О.В. Решение задач вычислительной математики в пакетах Mathcad 12, VFTLAB 7, Maple 9. М.: НТ Пресс, 2006. – 496 с. 3. Ляшенко М.Я., Головань М.С. Чисельні методи: Підручник. К.: Либідь. 1996. – 288 с. Лабораторна робота
|

 -го наближення на поточній
-го наближення на поточній  . (11)
. (11) стає непотрібною.
стає непотрібною.

 2.
2. 
 4.
4. 
 6.
6. 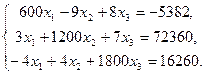
 8.
8. 
 10.
10. 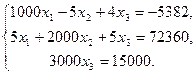
 12.
12. 
 14.
14. 
 16.
16. 
 18.
18. 
 20.
20. 



