Дифференциальные уравнения первого порядка. Дифференциальными уравнениями первого порядка называются уравнения вида .
Дифференциальными уравнениями первого порядка называются уравнения вида Определение. Решением дифференциального уравнения называется всякая функция Определение. Общим решением дифференциального уравнения первого порядка называется функция Перечислим основные типы уравнений и укажем способы их решения: 1) дифференциальное уравнение первого порядка с разделяющимися переменными - это уравнение вида:
Решается это уравнение делением его обеих частей на 2) однородное дифференциальное уравнение. Функция Дифференциальное уравнение называется однородным, если функция 3) линейное уравнение. Дифференциальное уравнение вида
называется линейным дифференциальным уравнением первого порядка. Оно сводится к двум уравнениям с разделяющимися переменными подстановкой:
Пример. Найти общее решение дифференциального уравнения Решение. Преобразуем наше уравнение следующим образом:
Это уравнение с разделяющимися переменными. Разделив обе части последнего равенства на
Интегрируя обе части уравнения, получим:
Последнее равенство задает нам решение в виде неявной функции Пример. Найти общее решение дифференциального уравнения Решение. Преобразуем уравнение к следующему виду:
Если правую часть последнего уравнения обозначить через
Следовательно, рассматриваемое уравнение является однородным. Положим теперь Разделяем переменные в последнем уравнении, деля его на
Отсюда Здесь мы вместо константы
Последнее равенство может давать не все решения, часть из них могли потеряться при разделении переменных (мы делили уравнение на
Пример. Найти общее решение линейного дифференциального уравнения Решение. Это линейное уравнение, поэтому его общее решение будем искать в виде
Функцию
Последнее уравнение неявно задает две серии функций:
Так как нам достаточно взять какое-то частное решение, то положим В этом случае наше уравнение перепишется так:
Учитывая, что
|

 .
.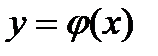 , которая, будучи подставлена в уравнение, превращает его в тождество.
, которая, будучи подставлена в уравнение, превращает его в тождество.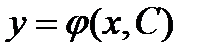 , которая является решением при каждом фиксированном С из некоторого множества М, и для любого решения
, которая является решением при каждом фиксированном С из некоторого множества М, и для любого решения  существует такое значение С1 из М, что
существует такое значение С1 из М, что 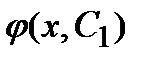 =
=  .
. и затем интегрированием;
и затем интегрированием; , называемая однородной степени
, называемая однородной степени  , если для любого
, если для любого 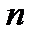 выполняется условие:
выполняется условие:  .
.
 , где
, где  - новая неизвестная функция, сводится к уравнению с разделяющимися переменными.
- новая неизвестная функция, сводится к уравнению с разделяющимися переменными.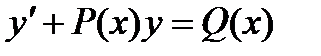 (2)
(2) где
где  и
и  - новые неизвестные функции.
- новые неизвестные функции. .
. ;
;  .
. получим:
получим: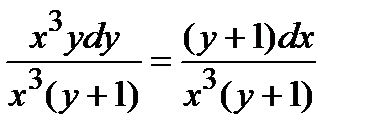 ;
; 
 ;
;  ;
; ;
; 
 . Обратим внимание на то что, что не все решения задаются указанным равенством. При делении на
. Обратим внимание на то что, что не все решения задаются указанным равенством. При делении на  и
и  Очевидно (подставьте в уравнение), что
Очевидно (подставьте в уравнение), что  является решением, а
является решением, а 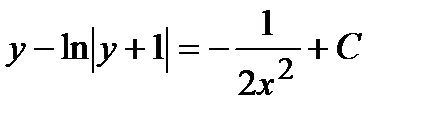 и
и  .
. ;
;  .
. , то
, то =
=  =
=  =
= 
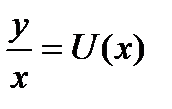 , или
, или  . Подставляя в уравнение выражения для у и
. Подставляя в уравнение выражения для у и  , получим:
, получим: 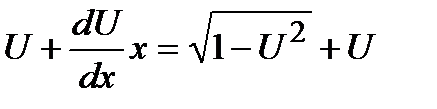 ;
;  ;
; 
 , и интегрируем полученное равенство:
, и интегрируем полученное равенство: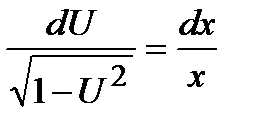 ;
; 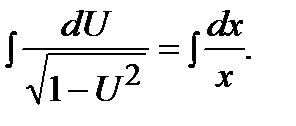
 , или
, или  .
. для удобства добавили константу
для удобства добавили константу 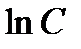 . Заменяя
. Заменяя 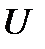 на
на  , получим решение:
, получим решение:
 и
и 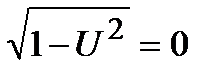 . Но
. Но  получаем, что
получаем, что  , или
, или  . Непосредственной подстановкой в уравнение убеждаемся, что функции
. Непосредственной подстановкой в уравнение убеждаемся, что функции  являются решениями. В нашем случае все решения задаются тремя формулами:
являются решениями. В нашем случае все решения задаются тремя формулами: ;
;  и
и 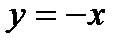 .
.
 . Тогда
. Тогда
 Подставляя у и
Подставляя у и  в уравнение, получим:
в уравнение, получим:
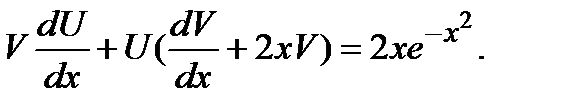
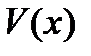 найдем из того условия, что выражение в скобке в последнем равенстве должно обращаться в ноль:
найдем из того условия, что выражение в скобке в последнем равенстве должно обращаться в ноль:
 .
.
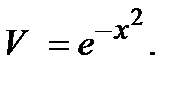

 получим общее решение уравнения
получим общее решение уравнения 



