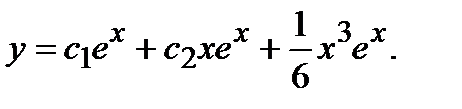Общее решение линейного неоднородного дифференциального уравнения  можно записать в виде
можно записать в виде 
 где
где  - общее решение соответствующего однородного дифференциального уравнения, а Y - частное решение данного неоднородного уравнения.
- общее решение соответствующего однородного дифференциального уравнения, а Y - частное решение данного неоднородного уравнения.
Функция Y может быть найдена методом неопределенных коэффициентов в следующих простейших случаях:
1) 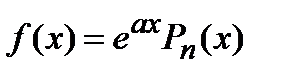 , где
, где  многочлен степени
многочлен степени  .
.
Если 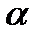 не является корнем характеристического уравнения, то частное решение ищут в виде
не является корнем характеристического уравнения, то частное решение ищут в виде  , где
, где 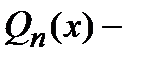 многочлен степени
многочлен степени  с неизвестными коэффициентами.
с неизвестными коэффициентами.
Если  - корень характеристического уравнения кратности
- корень характеристического уравнения кратности
 , то
, то 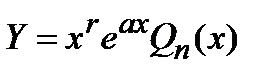 .
.
2) 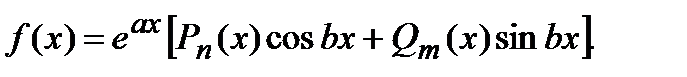
Если 
 не является корнем характеристического уравнения, то полагают
не является корнем характеристического уравнения, то полагают  ,
,
где 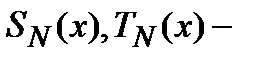 многочлены степени
многочлены степени  .
.
Если 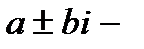 корни характеристического уравнения кратности
корни характеристического уравнения кратности  (для уравнений второго порядка
(для уравнений второго порядка  ), то полагают
), то полагают  .
.
Функцию, находящуюся в правой части линейного неоднородного дифференциального уравнения с постоянными коэффициентами, имеющую вид 
принято называть специальной правой частью.
Пример. Найти общее решение уравнения
 .
.
Решение. Найдем общее решение  однородного дифференциального уравнения
однородного дифференциального уравнения  . Характеристическое уравнение
. Характеристическое уравнение  имеет корни
имеет корни  . Следовательно,
. Следовательно,  .
.
Правая часть уравнения равна  . Следовательно,
. Следовательно,  , и поскольку
, и поскольку  не является корнем характеристического уравнения, то
не является корнем характеристического уравнения, то  . Поэтому частное решение ищем в виде
. Поэтому частное решение ищем в виде  .
.
Дифференцируя Y два раза и подставляя производные в данное уравнение, получим

Сокращая на  и приравнивая коэффициенты при одинаковых степенях
и приравнивая коэффициенты при одинаковых степенях  левой и правой частей последнего равенства, находим:
левой и правой частей последнего равенства, находим:
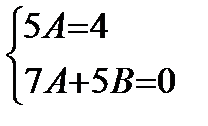

Отсюда  . Значит, общее решение данного уравнения имеет вид
. Значит, общее решение данного уравнения имеет вид
 .
.
Пример. Найти общее решение уравнения  .
.
Решениe. Найдем общее решение  однородного дифференциального уравнения
однородного дифференциального уравнения  .
.
Характеристическое уравнение  имеет корни
имеет корни  (кратность корня
(кратность корня  ). Следовательно,
). Следовательно,  .
.
Правая часть уравнения имеет вид 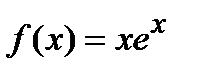 . Тогда
. Тогда 
 . Так как
. Так как 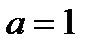 совпадает с корнем
совпадает с корнем  кратности
кратности  , то частное решение ищем в виде
, то частное решение ищем в виде  .
.
Дифференцируя Y два раза, подставляя в уравнение и приравнивая коэффициенты, получим:  .
.
Общее решение данного уравнения имеет вид
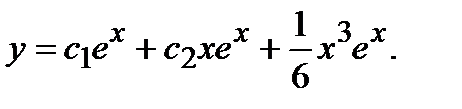

 можно записать в виде
можно записать в виде 
 где
где  - общее решение соответствующего однородного дифференциального уравнения, а Y - частное решение данного неоднородного уравнения.
- общее решение соответствующего однородного дифференциального уравнения, а Y - частное решение данного неоднородного уравнения.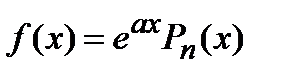 , где
, где  многочлен степени
многочлен степени  .
.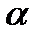 не является корнем характеристического уравнения, то частное решение ищут в виде
не является корнем характеристического уравнения, то частное решение ищут в виде  , где
, где 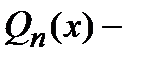 многочлен степени
многочлен степени  - корень характеристического уравнения кратности
- корень характеристического уравнения кратности , то
, то 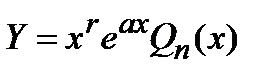 .
.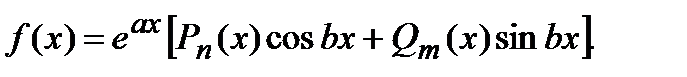

 ,
,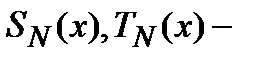 многочлены степени
многочлены степени  .
.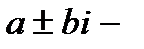 корни характеристического уравнения кратности
корни характеристического уравнения кратности  (для уравнений второго порядка
(для уравнений второго порядка  ), то полагают
), то полагают  .
.
 .
. однородного дифференциального уравнения
однородного дифференциального уравнения  . Характеристическое уравнение
. Характеристическое уравнение  имеет корни
имеет корни  . Следовательно,
. Следовательно,  .
. . Следовательно,
. Следовательно,  , и поскольку
, и поскольку  не является корнем характеристического уравнения, то
не является корнем характеристического уравнения, то  . Поэтому частное решение ищем в виде
. Поэтому частное решение ищем в виде  .
.
 и приравнивая коэффициенты при одинаковых степенях
и приравнивая коэффициенты при одинаковых степенях  левой и правой частей последнего равенства, находим:
левой и правой частей последнего равенства, находим: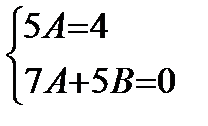

 . Значит, общее решение данного уравнения имеет вид
. Значит, общее решение данного уравнения имеет вид .
. .
. однородного дифференциального уравнения
однородного дифференциального уравнения  .
. имеет корни
имеет корни  (кратность корня
(кратность корня  ). Следовательно,
). Следовательно,  .
.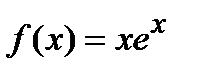 . Тогда
. Тогда 
 . Так как
. Так как 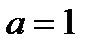 совпадает с корнем
совпадает с корнем  кратности
кратности  , то частное решение ищем в виде
, то частное решение ищем в виде  .
. .
.