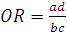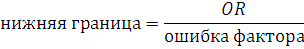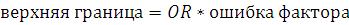Таблицы сопряженности
Теперь мы подошли к методам работы с таблицами типа «2×2» (такие таблицы называют «два–на–два», таблицы сопряженности). Это – краеугольный камень всех эпидемиологических исследований. Часто это первое, с чего начинают, приступая к изучению каких-либо данных. Таблица типа 2×2 (сопряженности) выглядит таким образом:
где: a = количество больных людей, кто подвергся воздействию фактора риска, b = количество больных людей, кто не подвергся воздействию фактора риска, c = количество здоровых людей, кто подвергся воздействию фактора риска, d = количество здоровых людей, кто не подвергся воздействию фактора риска, a + с = общее число, подвергшихся воздействию фактора риска, b + d = общее число не подвергшихся воздействию фактора риска, a + b = общее число случаев (больных людей), c + d = общее число контролей (здоровых людей).
Называя эти таблицы 2×2, можно заметить, что на самом деле, это таблицы 3×3, но поскольку колонки и строки с суммарными величинами не несут никакой самостоятельной информации, мы оставляем их просто как колонки и строки. Расположение строк и столбцов этой таблицы должно находиться в определенном порядке для того, чтобы показатели, рассчитанные из нее в дальнейшем, имели смысл и могли быть корректно интерпретированы. В первой строке всегда должны быть записаны результаты, касающиеся группы, в которой имел место исследуемый фактор воздействия. Говоря простым языком, первая строка отводится для группы, на которую было оказано исследуемое воздействие или объекты которой имели исследуемый фактор риска. Вторая строка содержит результаты контрольной группы, хотя это не всегда действительно контрольная группа в строгом смысле этого термина. Как правило, это группа, где исследуемый фактор риска отсутствовал. Иначе говоря, первой должна быть группа, представляющая исследовательский интерес, т.е. та группа, объекты которой подвергались (или наоборот не подвергались, если нас интересует не наличие, а отсутствие воздействия) фактору риска или какому-то другому воздействию, влияние которого нам надо исследовать. Во второй строке должны быть результаты, полученные в той группе, с которой будет происходить сравнение эффекта. Аналогично, в первом столбце записывается, сколько раз интересующее нас событие или явление было зарегистрировано в первой и второй группах, во втором столбце – сколько раз оно отсутствовало, т.е. результаты, касающиеся интересующего нас события должны находиться в первом столбце. Таблица сопряженности признаков позволяет выявить наличие связи между двумя признаками объекта, а также между фактором риска и исследуемым событием, которое по гипотезе должно быть связано с ним. Такие признаки называются дихотомическими, т.е. принимающими только два значения. Это очень важно отметить, поскольку метод нацелен именно на изучение связи между такими признаками. Как правило, это наличие или отсутствие какого-то фактора, но в целом любой показатель, даже имеющий непрерывную числовую шкалу (continuous data), можно преобразовать в дихотомический признак, определив точку разбиения его шкалы на две части, то есть проведя стратификацию, например: ИМТ>=26 и ИМТ<26, равносильно нашему качественному параметру, принимающему значения: «ожирение есть» и «ожирения нет». Этот нехитрый прием позволяет применять данный метод достаточно широко, не заботясь о параметрических характеристиках выборок. Мы не можем подсчитать риск на основании этой таблицы, так как это неприемлемо – вычисление рисков требует полного знания о количестве подвергшихся воздействию и о количестве случаев. У нас есть только небольшая группа случаев и группа контролей, и мы можем рассуждать только об этих группах. Как уже было указано выше в определении, если OR равно 1, это значит, что шансы заболеть равны и у тех, кто не подвергался воздействию фактора риска, и у тех, кто подвергался его воздействию. Таким образом, можно считать, что при OR = 1 заболевание не связано с данным фактором риска. Формула для вычисления OR может быть несколько преобразована в более простую для вычисления:
Задача: Обнаружено 10 человек больных тропической малярией. Для проведения исследования была отобрана контрольная группа, включающая 1000 человек, которые также проживали в этом же районе в этот период времени. Оказалось, что в контрольной группе укушены комарами были 400 человек.
Составляем таблицу сопряженности:
Среди больных шанс заболеть тропической малярией после укуса комара составляет a/b=8/2=4, а среди здоровых лиц из контрольной группы c/d=400/600=0,67. Соответственно, OR = 4/0,67 = 5,97. Гораздо легче воспользоваться упрощенной формулой:OR = ad/bc = 6. Вывод: Укус комара увеличивает риск заболеть тропической малярией в 6 раз. Ограничения при расчете OR: Для каждого числа из таблицы 2×2 существует статистическая неопределенность, которая отражается на действительной величине OR. Если мы повторим это исследование на других группах случаев и контролей (опросим других людей), то и цифры в ответах на вопросы будут отличаться. Идеального «истинного» отношения шансов для каждого фактора риска не существует. Принципиально это достижимо только в случае интервью всех случаев (при условии истинной диагностики бессимптомных форм заболевания) и всех контролей. Если так случилось, что цифры в квадратах a или d из таблицы 2×2 завышены по сравнению с тем, какими они «должны быть», то величина OR, которую мы подсчитаем, будет слишком высокой. И наоборот, если b и c слишком большие, величина OR окажется заниженной. Точные значения OR зависят от выбранных групп. Тот факт, что выбор групп для исследования из большой популяции подразумевает некоторую неопределенность, и приводит к необходимости применения статистических методов для эпидемиологии. Вероятный диапазон достоверных значений OR может быть достаточно легко подсчитан с помощью таблицы типа 2×2. Для каждого из наших пяти значений OR мы сначала вычисляем то, что называется ошибкой фактора, следующим образом:
где е – натуральный логарифм (= 2.71828); число 1,96 необходимо для того, чтобы быть уверенным, что существует 95% статистическая вероятность того, что в интервале между нижней и верхней границами находится истинное значение OR, вне зависимости от выбранных для исследования групп. Эта формула может показаться сложной, однако все операции могут быть выполнены на простейшем калькуляторе. Нижняя граница возможного значения OR для фактора определяется путем деления нашего, вычисленного выше, значения OR для этого фактора на ошибку фактора:
Верхняя граница вычисляется путем умножения значения OR на ошибку фактора:
Рассчитанный интервал, заключенный между нижней и верхней границами, и есть 95% доверительным интервалом (95% CI). Согласно определению: ДИ (доверительный интервал) — диапазон колебаний истинных значений в популяции. Величины, полученные в исследованиях на выборке больных, отличаются от истинных величин в популяции вследствие влияния случайности. Так, 95% ДИ означает, что истинное значение величины с вероятностью в 95% лежит в пределах рассчитанного интервала. Доверительные интервалы помогают сориентироваться, соответствует ли данный диапазон значений представлениям читателя о клинической значимости эффекта и каких результатов можно ожидать, применив описанную методику на сходной группе больных. Величина ДИ характеризует степень доказательности данных (в то время как значение p указывает на вероятность отклонения нулевой гипотезы). Для того чтобы доверительный интервал имел числовое отображение условились, что он равен такому диапазону, в который попадает 95% параметров. Т.е., вероятность того что величина находится вне доверительного интервала меньше 5%. При этом это относится не к выборке, которую мы можем сплошь и поперек измерить, а к популяции, многие из членов которой нам не доступны. Иными словами этот термин можно интерпретировать следующим образом: «В результате анализа выбранных групп случаев и контролей, мы с 95% уверенностью можем утверждать, что истинное значение OR для всей популяции, находится в интервале между верхней и нижней границами». Примечание. Описанный выше способ вычисления доверительных интервалов можно применять только в том случае, если все величины в таблице 2×2 будут больше или равны 10. Если хотя бы одна величина будет меньше 10, то вычисленный доверительный интервал будет значительно уже. Для случаев, когда хотя бы одно из значений в таблице меньше 10, необходимо пользоваться точным критерием Фишера (обычно расчет проводят при помощи компьютерных программ, так как вычисление даже маленьких чисел в таблице сопряженности требует значительных затрат времени из-за необходимости подсчета факториалов). Также необходимо отметить, что для расчетов по этой формуле необходимо знать абсолютные количества исследуемых, которые не могут быть заменены процентными соотношениями в группе. Следует заметить, что доверительные интервалы не рассчитываются для относительного риска, так как относительный риск подсчитывается точно для определенной группы (когортные исследования). Полученные результаты были истинными и не могли быть другими. В исследовании «случай-контроль» мы берем только небольшую выборку из генеральной совокупности, и с помощью доверительного интервала мы пытаемся оценить, насколько выбор случаев и контролей будет влиять на величину OR. Почти во всех эпидемиологических исследованиях мы изучаем ограниченную группу населения, а затем пытаемся экстраполировать полученные результаты на целую популяцию. Например, новые антибиотики испытывают на определенной группе пациентов, а затем их применяют на других группах больных с похожими заболеваниями. Или другой пример: время развития СПИДа у ВИЧ–инфицированных людей было изучено на одной группе пациентов, а затем, методом экстраполяции, перенесено на других ВИЧ-позитивных людей. Титры антител к вирусу кори были исследованы в ограниченной группе детей, а результаты были экстраполированы на всех детей этого возраста. В каждом из этих случаев мы не нуждались в доверительных интервалах, если хотели точно описать только те группы, которые мы изучали. Но поскольку обычно мы хотим применить результаты к более широким группам населения, то необходимо рассчитывать доверительные интервалы.
|