Для экономических специальностей заочной формы обучения. Задание 1. Решить задачу, используя классическое определение вероятности и правила комбинаторики.
ВЫСШАЯ МАТЕМАТИКА
Контрольная работа №3
Вариант А Задание 1. Решить задачу, используя классическое определение вероятности и правила комбинаторики. а) В урне содержатся 3 синих, 5 красных и 2 белых шара. Из нее наудачу извлекаются сразу два шара. Найти вероятность того, что будут вынуты либо два белых шара, либо два разных цветных шара. б) Наудачу взятый телефонный номер состоит из 5 цифр. Какова вероятность, что в нем все цифры разные? Решение. Вспомним классическое определение вероятности: вероятностью события А называется отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможныхнесовместных элементарных исходов, образующих полнуюгруппу:
Вероятность P(A) события А должна удовлетворять следующим условиям: 1о. P(A)= 1, если А – достоверное событие; 2о. P(A)= 0, если А – невозможное событие; 3о. 0< P(A)<;1, если А – случайное событие. Для подсчета вероятностей по классической формуле обычно используют методы комбинаторики. Комбинаторика – это раздел математики, посвященный решению задач выбора и расположения элементов в соответствии с каким-либо правилом. Существует две принципиально различные схемы выбора. В первой схеме выбор осуществляется без возвращения элементов. Это означает, что в выборке невозможны повторения элементов. Во второй схеме выбор осуществляется по-элементно с обязательным возвращением отобранного элемента при каждом шаге. Это означает, что в выборке возможны повторения. После того. как выбор тем или иным способом осуществлен, отобранные элементы могут быть либо упорядочены, либо неупорядочены. В первом случае, выборки, состоящие из одних и тех же элементов, но отличающиеся порядком следования этих элементов, объявляются различными. Во втором случае порядок следования элементов не принимается во внимание, и такие выборки объявляются тождественными.
а) Поскольку в данной задаче неважен порядок, то для решения будем применять сочетания без повторения (шары не возвращаются обратно в урну). Найдем общее число возможных исходов:
Теперь найдем число благоприятствующих возможных исходов. Два белых шара можно вынуть m 1=C22=1 способом, два разных цветных шара m 2=C31×C51=3×5=15 способами. Тогда общее число благоприятствующих исходов, в соответствии с принципом сложения, равно m = m 1+ m 2 = 16. Таким образом,
б) Всего имеется 10 цифр. Поскольку при составлении пятизначным номеров важен порядок и возможны повторения, то общее число возможных пятизначных номеров будет равно
Номера, у которых все цифры разные, – это размещения без повторений
Таким образом, искомая вероятность равна
Задание 2. Решить задачу, используя теоремы сложения и умножения вероятностей. а) Вероятность попадания в цель при отдельном выстреле (событие А) равна 0,8. Какова вероятность поражения цели, если в 2% случаях бывают осечки, т.е. в 2% случаях выстрела не происходит? б) Два стрелка делают по одному выстрелу по мишени. Вероятность попадания для первого стрелка равна 0,8, для второго – 0,7. Какова вероятность поражения цели? Решение. Вспомним теоремы сложения и умножения вероятностей. Теорема сложения вероятностей несовместных событий. P(A+B) = P(A) + P(B). Теорема сложения вероятностей совместных событий. P(A+B) = P(A)+P(B)–P(AB). Теорема умножения вероятностей независимых событий. P(AB) = P(A)P(B). Теорема умножения вероятностей зависимых событий. P(AB) = P(A)PA(B) = P(B)PB(A).
Достоверное событием обычно обозначается символом W, невозможное событие – символом Æ. Тогда
а) Пусть событие В состоит в том, что выстрел произошел, тогда событие P (AB) = P (B) PB (A) = 0,98×0,8 = 0,784. б) Пусть A 1={ первый стрелок попал по цели }, A 2={ второй стрелок попал по цели }. Мишень будет поражена (событие В), если произойдет событие А 1+ А 2. Поскольку события А 1 и А 2 совместны, но независимы, то P (А 1+ А 2) = P (А 1)+ P (А 2)– P (А 1) P (А 2) = 0,7+0,8–0,7×0,8 = 0,94. Отметим, что событие В можно записать также в виде A1 P(B) = P(A1)P(
Задание 3. Решить задачу, используя формулу полной вероятности или формулу Байеса. а) В первой урне находится 5 белых и 3 черных шара. Во второй – 4 белых и 5 черных шара. Из первой урны во вторую наугад перекладывают два шара. После этого из второй урны вынимают сразу 4 шара. Какова вероятность того, что шары будут одного цвета? б) Двое стрелков произвели по одному выстрелу по мишени. Вероятность попадания первым стрелком равна 0,8, вторым – 0,4. Мишень поражена одним попаданием. Определить вероятность того, что в мишень попал первый стрелок?
|




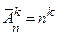
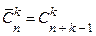





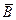 означает противоположное событие, т.е. что произошла осечка. По условию P (
означает противоположное событие, т.е. что произошла осечка. По условию P ( ) = 0,02, отсюда получаем P (B) = 1 –P (
) = 0,02, отсюда получаем P (B) = 1 –P ( +
+  A2+A1A2. Тогда получим
A2+A1A2. Тогда получим


