Приклади розв’язання стереометричних задач координатно-векторним методом
Задача 1 Основою піраміди SAΒCD є паралелограм. Проведено площину, що перетинає бічні ребра SA, SΒ, SC, SD піраміди відповідно в точках K, L, M, N таких, що
Розв’язання. За умовою належності чотирьох точок M, N, K і L, маємо:
Представимо кожен із векторів, що входять в рівність у вигляді різниці двох векторів зі спільним початком в точці S. Отримаємо:
де γ=1-α-β. Враховуючи умову задачі і попередню рівність перепишемо так
Позначимо через точку О перетин діагоналей паралелограма AΒCD. Так як О – середина діагоналей AC і ΒD, то
Таким чином, вектор В силу єдиності розкладу вектора, отримуємо числові рівності:
Звідси, враховуючи, що
Наведемо числовий приклад. Якщо площина проходить через вершину A тетраедра AΒCD і перетинає його ребра SΒ і SD в точках L і N таких, що Задача 2 (побудова і обчислення довжини спільного перпендикуляра) В кубі ABCDA1B1C1D1 з ребром
Розв’язання. Виберемо векторний базис
Тоді,
Знайдемо такі числа x і y, щоб вектор
Беручи до уваги, що
Точки P і Q шуканого спільного перпендикуляра будуються відповідно з отриманих рівностей Умова компланарності трьох векторів. Задача 3 На діагоналях АВ1 і ВС1 граней AA1B1B і ВВ1С1С паралелепіпеда ABCDA1B1C1D1 взяті точки відповідно Н і M так, що відрізки MН і A1C паралельні. Знайдіть відношення довжин цих відрізків. Розв’язання. Введемо вектори:
Трійку
Оскільки точка Н лежить на діагоналі АВ1, то вектори колінеарні, тому існує таке число х, що
За правилом ламаної знаходимо:
За умовою MН ׀׀A1C, значить, існує таке число t, що
Внаслідок некомпланарності векторів
Розв’язком цієї системи рівнянь є:
Відповідь: 1: 3. Скалярний добуток двох векторів Задача 4 Дано прямокутний паралелепіпед ABCDA1B1C1D1. Яке найбільше значення може приймати кут нахилу його діагоналі Розв’язання.
Виберемо в просторі прямокутну систему координат з початком в точці D. Рівняння площини
Вектор Знаходимо
З очевидної нерівності Звідки слідує, що:
і Таким чином, Отже, якщо
Величина кута між двома площинами обчислюється за визначенням від 0° до 90°. Якщо вектори
(даний кут або рівний куту між векторами
|



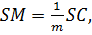

 Знайти залежність між числами k, l, m, n.
Знайти залежність між числами k, l, m, n.

 .
. ,
, .
. 2
2  .
.
 виражаємо двома способами через не компланарні вектори
виражаємо двома способами через не компланарні вектори  ,
,  і
і  .
. ,
, 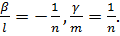
 , знаходим:
, знаходим: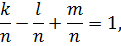
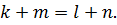
 ,
,  , то
, то  ,
,  ,
,  , значить
, значить  , тобто
, тобто  .
. знайдіть відстань між прямими AB1 і BC1.
знайдіть відстань між прямими AB1 і BC1.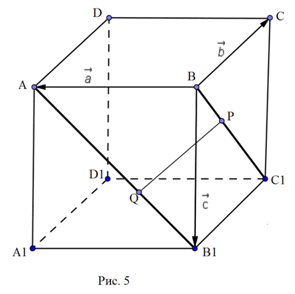
 , де
, де 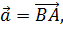
 ,
,  Нехай P і Q – деякі точки відповідно прямих BC1 і AB1. Нехай
Нехай P і Q – деякі точки відповідно прямих BC1 і AB1. Нехай 

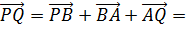

 був ортогональним векторам
був ортогональним векторам  і
і  , і т. д., щоб мали місце рівності:
, і т. д., щоб мали місце рівності:
 та, що
та, що  отримуємо систему:
отримуємо систему:
 ,
, 
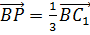 і
і 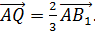 А так як
А так як 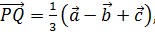 то
то 





 , некомпланарних векторів приймемо за базис і розкладемо вектори
, некомпланарних векторів приймемо за базис і розкладемо вектори  за векторами цього базису.Маємо:
за векторами цього базису.Маємо:

 Аналогічно, в силу колінеарності векторів
Аналогічно, в силу колінеарності векторів  існує таке число у, що
існує таке число у, що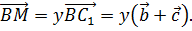

 тобто виконується рівність:
тобто виконується рівність:
 і єдиності розкладу вектора за базисом, приходимо до висновку:
і єдиності розкладу вектора за базисом, приходимо до висновку: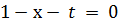 ,
,  ,
,  .
. Тоді
Тоді виходить, МН: СА1 = 1: 3.
виходить, МН: СА1 = 1: 3. до площини
до площини 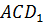 ?
?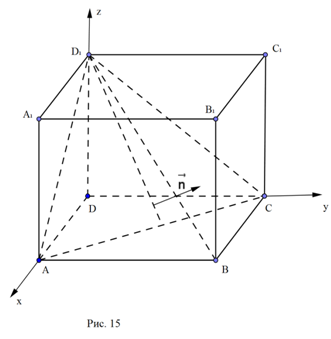

 перпендикулярний до площини
перпендикулярний до площини  . Позначимо шуканий кут через
. Позначимо шуканий кут через  . Легко довести, що
. Легко довести, що 
 Значить,
Значить,  де
де
 слідує, що
слідує, що 

 , причому
, причому  тоді і тільки тоді, коли
тоді і тільки тоді, коли 
 і
і  лише за умови, що паралелепіпед є кубом.
лише за умови, що паралелепіпед є кубом. – напрямний вектор даної прямої і
– напрямний вектор даної прямої і  – вектор, перпендикулярний до площини
– вектор, перпендикулярний до площини  то кут
то кут 
 і
і  – вектори перпендикулярні відповідно площинам
– вектори перпендикулярні відповідно площинам  і
і  то кут між даними площинами знаходиться з рівності
то кут між даними площинами знаходиться з рівності
 або доповнює його до 180°.)
або доповнює його до 180°.)


