Пример 6. Найти расстояние от точки до плоскости, проходящей через точки .
Найти расстояние от точки Найдем уравнение плоскости, проходящей через точки
Вычислим определитель, разложив его по первой строке:
Найдем расстояние от точки
Контрольные варианты к задаче 6 Найти расстояние от точки
З а д а ч а 7 Косинус угла
Пример 7 Найти угол между плоскостями Найдем косинус искомого угла:
Контрольные варианты к задаче 7 Найти угол между плоскостями: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
З а д а ч а 8 Канонические уравнения прямой в пространстве имеют вид
где Чтобы перейти от общих уравнений прямой
к ее каноническим уравнениям, нужно на прямой найти какую-нибудь точку линии пересечения плоскостей (10) и, следовательно, перпендикулярен векторам
|
до плоскости, проходящей через точки 
.
:
до плоскости 
.
:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
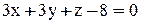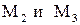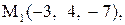
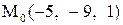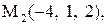
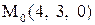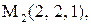
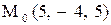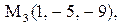
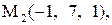
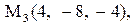
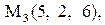
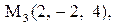
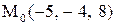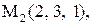
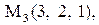
между плоскостями 
и 
вычисляется по формуле
.
.
, 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
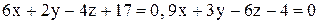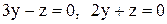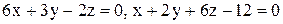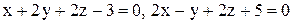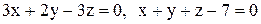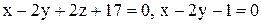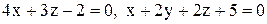, (9)
- точка, лежащая на прямой, а 
- направляющий вектор прямой (ненулевой вектор, параллельный прямой).
(10)
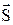. Точку 
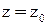, и из общих уравнений прямой (10) найдем значения 
. Направляющий вектор 
. Поэтому в качестве 
.
