Контрольная работа. 1. Методические указания к курсовому проектированию «Экономика и управление системами теплоэнергоснабжения» для студентов специальности «Энергообеспечение
1. Методические указания к курсовому проектированию «Экономика и управление системами теплоэнергоснабжения» для студентов специальности «Энергообеспечение предприятий» и экономических специальностей ЭУП, ФиК, МО всех форм обучения: ВолгГАСУ, Волгоград, 2008г. Контрольная работа «линейная алгебра» Вычислить определители а) Решение.Этот определитель вычислим по правилу диагоналей. Приписываем справа к определителю первый и второй столбцы. Перемножаем элементы, стоящие на главной диагонали и складываем это произведение с аналогичными произведениями элементов, стоящих на диагоналях, параллельных главной. Затем к произведению элементов, стоящих на побочной диагонали, прибавляем аналогичные произведения элементов, стоящих на диагоналях, параллельных побочной. Затем от первой суммы вычитаем вторую. Это и будет искомый определитель.
Ответ: Задача 1. Решить систему по формулам Крамера: запишем определитель системы Заменим в
Заменим в
По формулам Крамера получаем решение Ответ: Контрольные варианты к задаче 1. Решить системы по формулам Крамера:
Контрольная работа «Векторная алгебра и аналитическая геометрия» Задача 1. Если известны координаты точек Разложение этого вектора по ортам Длина вектора находится по формуле Пример 1. Даны точки Разложить вектор
Вектор Контрольные варианты к задаче 1. Даны точки А, В и С. Разложить вектор
Задача 2. Если даны векторы
Пример 2. Даны вершины треугольника
Проекция Контрольные варианты к задаче 2 Даны точки А, В и С из задания 1. Найти угол при вершине А и проекцию вектора Задача 3. Площадь параллелограмма, построенного на векторах можно найти по формуле на этих векторах: Определитель второго порядка вычисляется по формуле:
Пример 3. Даны вершины треугольника
Векторное произведение
Длина полученного вектора равна: Так как Контрольные варианты к задаче 3 Даны точки А, В и С из задания 1, которые являются вершинами Найти его площадь и длину высоты, опущенной из вершины С.
Задача 4. Если даны координаты
Объемы параллелепипеда и тетраэдра (треугольной пирамиды), построенных на векторах
Если Если Если Пример 4. Дан тетраэдр Объем
Вычислим векторное произведение
Тогда Контрольные варианты к задаче 4 1. Найти объем треугольной пирамиды, построенной на векторах
2. Найти объем треугольной пирамиды с вершинами
3. Найти объем треугольной пирамиды с вершинами:
4. Найти объем треугольной пирамиды, вершины которой находятся в точках
5. Найти объем треугольной пирамиды с вершинами 6. Найти объем треугольной пирамиды с вершинами в точках
7. Вершины треугольной пирамиды находятся в точках 8.Найти объем треугольной пирамиды, образованной векторами 9. Найти объем треугольной пирамиды, образованной векторами 10. Найти объем треугольной пирамиды, образованной векторами
Задача 5. Даны координаты вершин пирамиды 1. Найти длину вектора 2. Найти угол между векторами 3. Найти проекцию вектора 4. Найти площадь грани АВС. 5. Найти объем пирамиды ABCD. Координаты векторов: 1. Длина вектора
3. Проекция вектора
4.
5.
Контрольные варианты к задаче 5 Даны координаты вершин пирамиды ABCD. Требуется найти: 1) длины векторов 2) угол между векторами 3) проекцию вектора 4) площадь грани АВС; 5) объем пирамиды ABCD.
З а д а ч а 6 Общее уравнение плоскости имеет вид: Уравнение плоскости, проходящей через три данные точки
Векторы Расстояние от точки
|

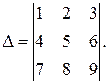




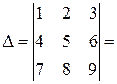


 .
.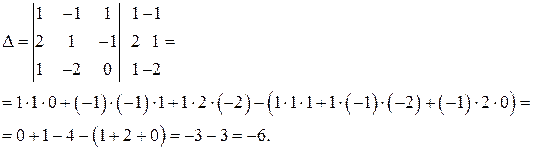
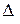 столбец коэффициентов при
столбец коэффициентов при 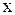 на столбец правых частей
на столбец правых частей

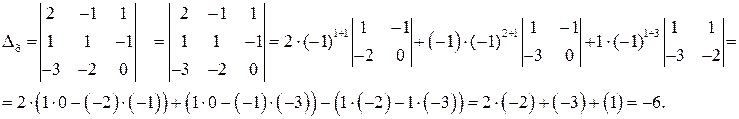 Заменим в
Заменим в 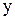 на столбец правых частей
на столбец правых частей

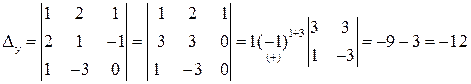
 на столбец правых частей
на столбец правых частей


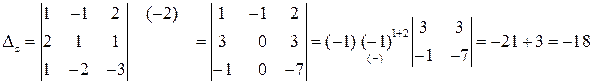 .
. .
.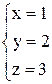 .
.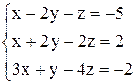 ;
;
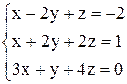 .
.
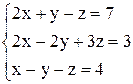 ;
;
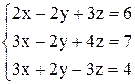 .
.
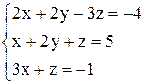 ;
;
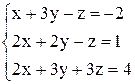 .
.
 ;
;
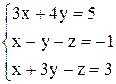 .
.
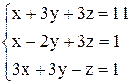 ;
;
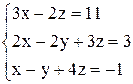 .
.
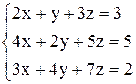 ;
;
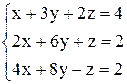 .
.
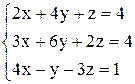 ;
;
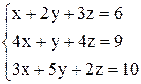 .
.
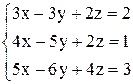 ;
;
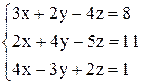 .
.
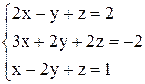 ;
;
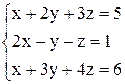 .
.
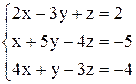 ;
;
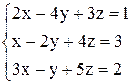 .
.
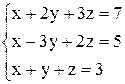 ;
;
 .
.
 ;
;
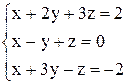 .
.
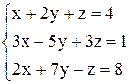 ;
;
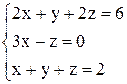 .
.
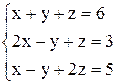 ;
;
 .
.
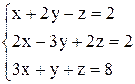 ;
;
 .
.
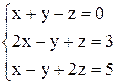 ;
;
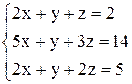 .
.
 и
и 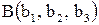 , то координаты вектора
, то координаты вектора 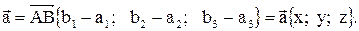
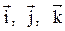 :
: 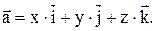
 а направляющие косинусы равны
а направляющие косинусы равны 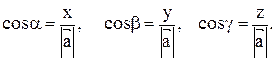 Орт вектора
Орт вектора 

 по ортам
по ортам 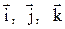 и найти его длину, направляющие косинусы, орт вектора
и найти его длину, направляющие косинусы, орт вектора 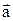 . Найдем координаты векторов:
. Найдем координаты векторов: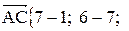
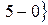
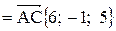 и
и 
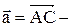
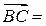
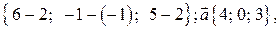

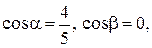
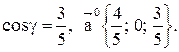
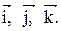 Найти длину, направляющие косинусы и орт вектора
Найти длину, направляющие косинусы и орт вектора 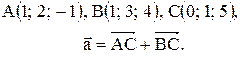
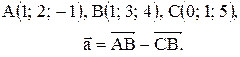
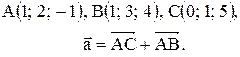
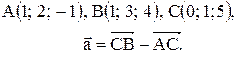
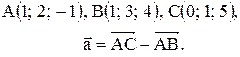
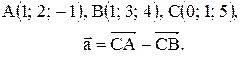
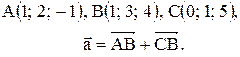
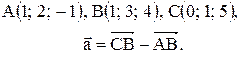
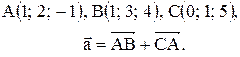
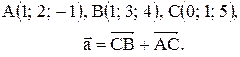

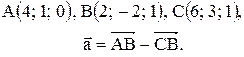
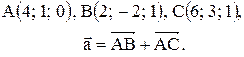

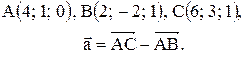
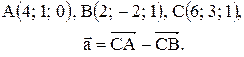

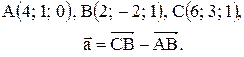
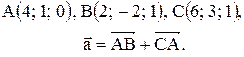
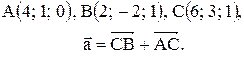
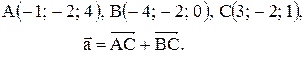
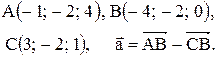
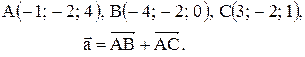
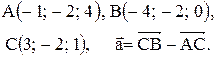
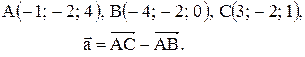
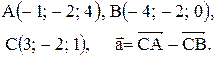
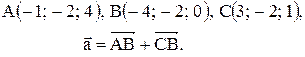
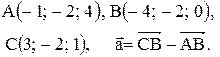

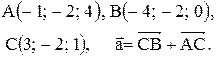
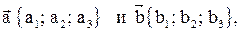 то скалярное произведение
то скалярное произведение  .
.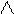 Тогда
Тогда 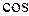
 ; проекция вектора
; проекция вектора 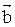 на направление вектора
на направление вектора 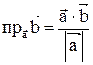 , условие перпендикулярности ненулевых векторов выглядит следующим образом:
, условие перпендикулярности ненулевых векторов выглядит следующим образом: 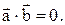 Условие коллинеарности векторов:
Условие коллинеарности векторов: 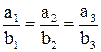 .
.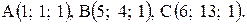 Найти угол при вершине А и проекцию вектора
Найти угол при вершине А и проекцию вектора 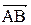 на сторону АС. С
на сторону АС. С
 Внутренний угол при вершине А образован векторами
Внутренний угол при вершине А образован векторами 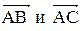 ,
, А В
А В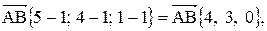
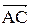
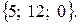
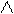 Тогда
Тогда 
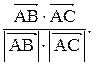
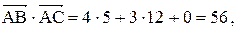
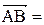
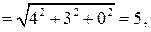
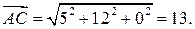
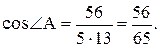
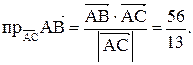
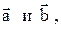
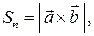 а площадь треугольника, построенного
а площадь треугольника, построенного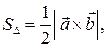 где
где 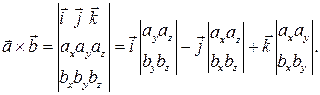
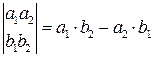 .
.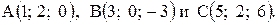 Найти его площадь и длину высоты, опущенной из вершины С.
Найти его площадь и длину высоты, опущенной из вершины С.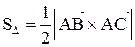 . Находим векторы
. Находим векторы 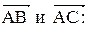
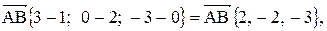
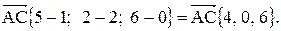

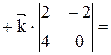
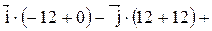
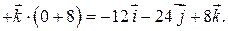
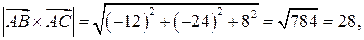
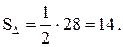
 где
где 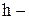 длина высоты, опущенной из вершины С на сторону АВ,
длина высоты, опущенной из вершины С на сторону АВ, 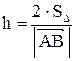 .
. 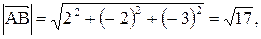
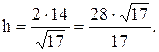
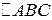 .
.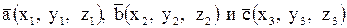 , то смешанное произведение векторов вычисляют по формуле
, то смешанное произведение векторов вычисляют по формуле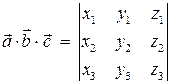 .
.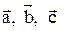 находятся с помощью смешанного произведения векторов:
находятся с помощью смешанного произведения векторов: ,
, 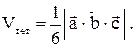
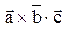 > 0, то тройка векторов
> 0, то тройка векторов 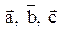 - правая.
- правая.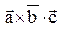 < 0, то тройка левая.
< 0, то тройка левая.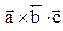 = 0, то векторы
= 0, то векторы  компланарны.
компланарны.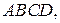 построенный на векторах
построенный на векторах 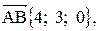
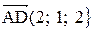 и
и 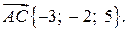 Найти высоту, проведенную из вершины
Найти высоту, проведенную из вершины 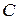 на грань ABD.
на грань ABD.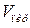 равен произведению площади основания на высоту:
равен произведению площади основания на высоту:
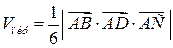 , поэтому
, поэтому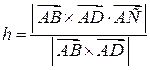 .
.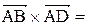
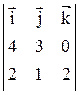 =
=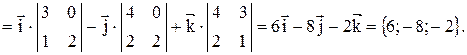
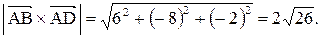

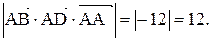
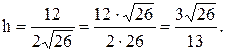
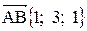 ,
,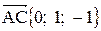 и
и 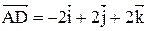 .
. ,
, 
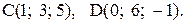

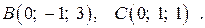
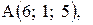
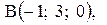
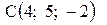 и
и 
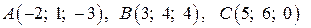 .
.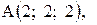
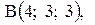
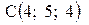 и
и 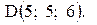

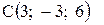 и
и 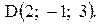
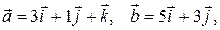
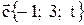 .
.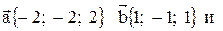
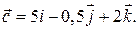
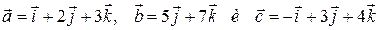 .
.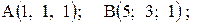
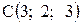 ;
; 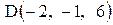 .
.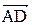 .
.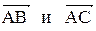 .
.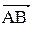 .
.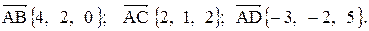
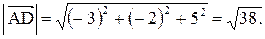
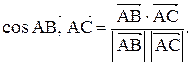
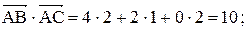


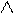
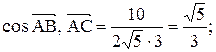
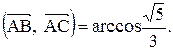
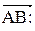
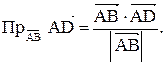
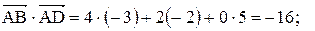
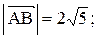
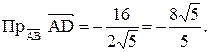
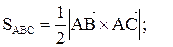
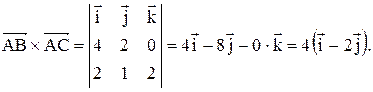
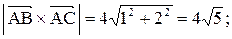
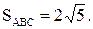
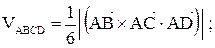
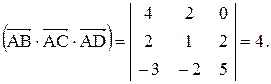
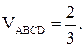

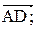

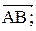
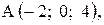
 ,
,
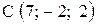 ,
,
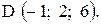
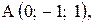
 ,
,
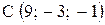 ,
,
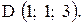
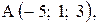
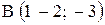 ,
,
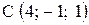 ,
,
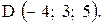
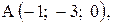
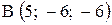 ,
,
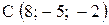 ,
,
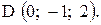
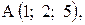
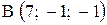 ,
,
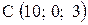 ,
,
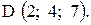
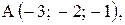
 ,
,
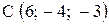 ,
,
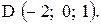
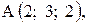
 ,
,
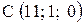 ,
,
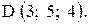
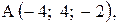
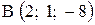 ,
,
 ,
,
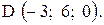
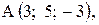
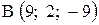 ,
,
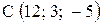 ,
,
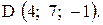
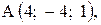
 ,
,
 ,
,
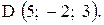

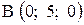 ,
,
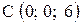 ,
,
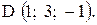

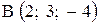 ,
,
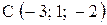 ,
,
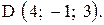
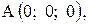
 ,
,
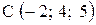 ,
,

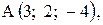
 ,
,
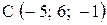 ,
,
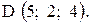
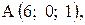
 ,
,
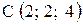 ,
,
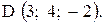
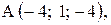
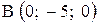 ,
,
 ,
,
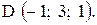
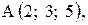
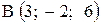 ,
,
 ,
,
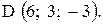
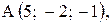
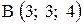 ,
,
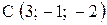 ,
,
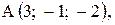
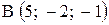 ,
,
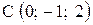 ,
,
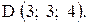
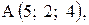
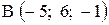 ,
,
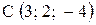 ,
,
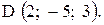
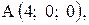
 ,
,
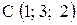 ,
,
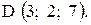
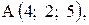
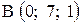 ,
,
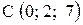 ,
,
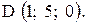
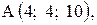
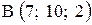 ,
,
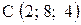 ,
,
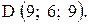
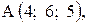
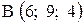 ,
,
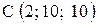 ,
,
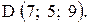
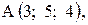
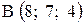 ,
,
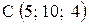 ,
,
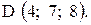
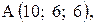
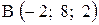 ,
,
 ,
,
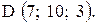
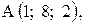
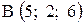 ,
,
 ,
,
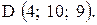
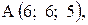
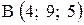 ,
,
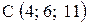 ,
,
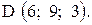

 ,
,
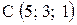 ,
,
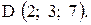
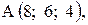
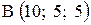 ,
,
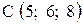 ,
,
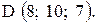
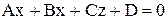 , где
, где 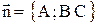 - ненулевой вектор, перпендикулярный плоскости (нормальный вектор плоскости).
- ненулевой вектор, перпендикулярный плоскости (нормальный вектор плоскости).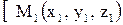 ,
, 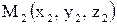 и
и 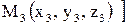 определяется равенством
определяется равенством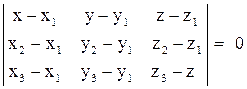 ,т.к.
,т.к.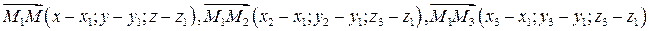 лежат в одной плоскости, т.е. их смешанное произведение равно нулю
лежат в одной плоскости, т.е. их смешанное произведение равно нулю 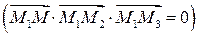 . Точка
. Точка 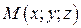 является текущей,т.е. произвольной точкой плоскости.
является текущей,т.е. произвольной точкой плоскости.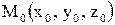 до плоскости
до плоскости  .
.


