Я взяла сайт для анализа страниц http://pr-cy.ru/a/cooklib.ru / В нем были следующие данные:
URL: cooklib.ru
Заголовок: Кулинарная Копилка
Описание: несложные кулинарные рецепты домашней кухни на праздник и на каждый день: салаты и закуски, супы, вторые блюда, выпечка, десерты, детская кухня. Есть коллекции рецептов блюд для горшочков, пароварки, рецепты хлеба для хлебопечки. А также советы кулинару.
Ключевые слова: запеканки, салаты, закуски, супы, вторые блюда, выпечка, десерты, кухни мира, фото-рецепт, легкие салаты, рецепт, творог, шарлотка, детская кухня
Кодировка: windows-1251
Размер страницы: 22Кб
Скорость загрузки сайта: 3,67 сек
IP сервера: 87.255.0.158
Расположение сервера: Россия 
Тоже самое я проделала и со вторым сайтом http://pr-cy.ru/a/arngren.net В нем были следующие данные:
URL: http://arngren.net
Заголовок: Отсутствует
Описание: нет
Ключевые слова: elbil, elsykkel, kamera, oversetter, translatшr, translator, dictionary, moped, fordelere, styreenhet, scooter, el-scooter, el-moped, solselle ryggsekk, solcelle-ryggsekk, ryggsekk, el-sykkel, el stkkel, elektrisk sykkel, elbil, rc helikopter, rc produkter, el bil, elektrisk bil, elektriskbil, el kjшretшy,, elkjшretшy, elektrisk kjшretшy, ATV, jeep, el-jeep, bil, omformer, www.arngren.net, TV, TV med DVD, elektronikk,roboter,hobby,gaver,data,dvd,conrad,teknikk,pc,alkotester,modellhobby,byggese
Кодировка: ISO-8859-1
Размер страницы: 632 Кб.
Скорость загрузки сайта: 5,45 сек
IP сервера: 67.195.61.65
Расположение сервера: Дания
Адрес этой страницы: http://arngren.net
| Рисунок 3.4- анализ сайтов
| |
Вывод:
В ходе работы был проведен анализ 2 сайтов, произведено их сравнение
Знакоопределенные квадратичные формы.
Критерий Сильвестра.
Определение. Квадратичная функция на линейном пространстве L называется положительно определенной, если; отрицательно определенной, если.
Пусть в некотором базисе квадратичная функция записана в виде квадратичной формы
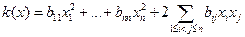 (1)
(1)
с матрицей 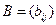
Лемма. Квадратичная форма тогда и только тогда является положительно определенной, когда она приводится к диагональному виду
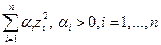 (2)
(2)
⇔
к каноническому виду 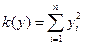 . (3)
. (3)
Замечание. От вида (2) к каноническому виду (3) можно перейти в результате замены 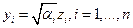 .
.
Доказательство леммы. То, что диагональная форма со всеми положительными коэффициентами или каноническая форма 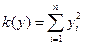 является положительно определенной, ясно.
является положительно определенной, ясно.
Обратно, допустим, что данная положительно определенная квадратичная форма 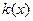 имеет канонический вид
имеет канонический вид  . Если, вопреки доказываемому,
. Если, вопреки доказываемому, 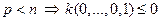 , что противоречит положительной определенности. ð
, что противоречит положительной определенности. ð


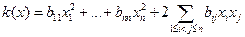 (1)
(1)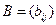
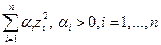 (2)
(2)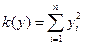 . (3)
. (3)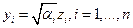 .
.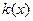 имеет канонический вид
имеет канонический вид  . Если, вопреки доказываемому,
. Если, вопреки доказываемому, 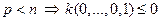 , что противоречит положительной определенности. ð
, что противоречит положительной определенности. ð


