Достаточность: дано, что все главные миноры матрицы квадратичной формы положительны, надо доказать, что она является положительно определенной.
Воспользуемся методом математической индукции и леммой.
Для 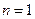 достаточность очевидна.
достаточность очевидна.
Допустим, что  и из положительности главных миноров матрицы квадратичной формы порядка до
и из положительности главных миноров матрицы квадратичной формы порядка до 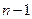 включительно следует возможность приведения квадратичной формы от
включительно следует возможность приведения квадратичной формы от 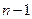 переменных
переменных  к виду
к виду  .
.
Покажем, что в этом случае достаточность будет иметь место и для квадратичной
формы, зависящих от n переменных.
В выражении для квадратичной формы, зависящей от n переменных  , выделим слагаемые, содержащие
, выделим слагаемые, содержащие  :
:
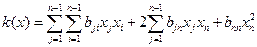 .
.
Двойная сумма  в правой части этого равенства есть квадратичная форма
в правой части этого равенства есть квадратичная форма  , зависящая от
, зависящая от 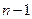 переменной, причем главные миноры её матрицы совпадают с главными минорами
переменной, причем главные миноры её матрицы совпадают с главными минорами 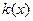 до порядка
до порядка 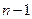 включительно, которые, по условию, положительны. Отсюда следует, по предположению индукции, что квадратичная форма
включительно, которые, по условию, положительны. Отсюда следует, по предположению индукции, что квадратичная форма  положительно определенная и для неё существует невырожденная замена переменных
положительно определенная и для неё существует невырожденная замена переменных
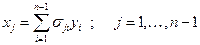 ,
,
приводящая её к каноническому виду:  .
.
Запишем квадратичную форму 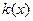 в новых переменных (пока не заменяя xn):
в новых переменных (пока не заменяя xn):

и выделим полные квадраты по  :
:
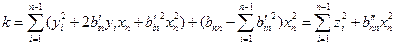 ,
,
где  .
.
В матричном виде эту замену переменных можно записать как
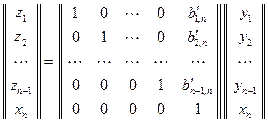
и поскольку определитель ее матрицы отличен от нуля, то эта замена невырожденная.
Наконец, вспомним, что определитель матрицы квадратичной формы сохраняет знак при замене базиса. Определитель матрицы B квадратичной функции в исходном базисе положительный, поскольку этот определитель является главным минором порядка n. Но из выражения для 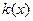 в конечном базисе мы получаем, что определитель матрицы квадратичной формы
в конечном базисе мы получаем, что определитель матрицы квадратичной формы  равен
равен 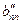 . Поэтому
. Поэтому  и можно ввести переменную
и можно ввести переменную  , в результате чего получаем канонический вид квадратичной формы
, в результате чего получаем канонический вид квадратичной формы
 .
.
Следовательно, квадратичная функция 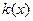 положительно определена.
положительно определена.
Достаточность доказана.
Необходимость.
Дано, что квадратичная функция положительно определенна, и надо доказать положительность главных миноров ее матрицы. Снова применим индукцию по числу переменных n.
Для 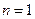 это ясно.
это ясно.
Пусть  и для форм от меньшего числа переменных утверждение теоремы верно.
и для форм от меньшего числа переменных утверждение теоремы верно.
Поскольку квадратичная форма  из доказательства достаточности также является положительно определенной (ее значения – это значения
из доказательства достаточности также является положительно определенной (ее значения – это значения 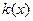 при
при  ), то по предположению индукции ее главные миноры, совпадающие с главными минорами матрицы B до порядка
), то по предположению индукции ее главные миноры, совпадающие с главными минорами матрицы B до порядка 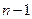 , положительны. А определитель самой матрицы B, который является главным минором порядка n, положителен, поскольку
, положительны. А определитель самой матрицы B, который является главным минором порядка n, положителен, поскольку 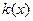 приводится к каноническому виду
приводится к каноническому виду  , и определитель матрицы полученной при этом квадратичной формы равен 1 и имеет такой же знак, как и определитель матрицы B.
, и определитель матрицы полученной при этом квадратичной формы равен 1 и имеет такой же знак, как и определитель матрицы B.
Теорема полностью доказана. ð
Следствие. (Критерий отрицательной определенности). Для отрицательной определенности квадратичной формы 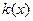 в
в  необходимо и достаточно, чтобы все главные миноры её матрицы B имели чередующиеся знаки, начиная с минуса, т.е.
необходимо и достаточно, чтобы все главные миноры её матрицы B имели чередующиеся знаки, начиная с минуса, т.е.  .
.
Доказательство. Рассмотрим квадратичную форму 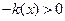 с матрицей
с матрицей  : для нее, по критерию Сильвестра,
: для нее, по критерию Сильвестра,
Ч.т.д.

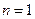 достаточность очевидна.
достаточность очевидна. и из положительности главных миноров матрицы квадратичной формы порядка до
и из положительности главных миноров матрицы квадратичной формы порядка до 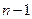 включительно следует возможность приведения квадратичной формы от
включительно следует возможность приведения квадратичной формы от  к виду
к виду  .
. , выделим слагаемые, содержащие
, выделим слагаемые, содержащие  :
: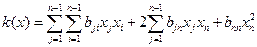 .
. в правой части этого равенства есть квадратичная форма
в правой части этого равенства есть квадратичная форма  , зависящая от
, зависящая от 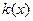 до порядка
до порядка 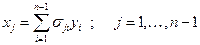 ,
, .
.
 :
: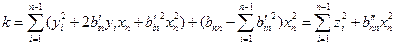 ,
, .
.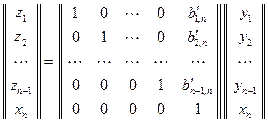
 равен
равен 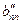 . Поэтому
. Поэтому  и можно ввести переменную
и можно ввести переменную  , в результате чего получаем канонический вид квадратичной формы
, в результате чего получаем канонический вид квадратичной формы .
. ), то по предположению индукции ее главные миноры, совпадающие с главными минорами матрицы B до порядка
), то по предположению индукции ее главные миноры, совпадающие с главными минорами матрицы B до порядка  необходимо и достаточно, чтобы все главные миноры её матрицы B имели чередующиеся знаки, начиная с минуса, т.е.
необходимо и достаточно, чтобы все главные миноры её матрицы B имели чередующиеся знаки, начиная с минуса, т.е.  .
.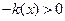 с матрицей
с матрицей  : для нее, по критерию Сильвестра,
: для нее, по критерию Сильвестра,


