Задача № 9.
9.1. Дана функция распределения случайной величины X:
Найти вероятность попадания случайной величины X в интервал 9.2. График плотности распределения непрерывной случайной величины X имеет вид
Найти функции f(x) и F(х). Вычислить М[Х]. x -2 0 4 9.3. График плотности распределения непрерывной случайной величины Xимеет вид Найти математическое ожидание,
ческое отклонение. 0 2 x 9.4.Случайная величина X задана плотностью распределения 9.5. Дана плотность распределения непрерывной случайной величины X: Найти коэффициент A. Определить математическое ожидание и среднее квадратическое отклонение. 9.6. Случайная величина X распределена по "Закону прямоугольного треугольника" в интервале (0, а). f(x)
x 0 а Написать выражение плотности распределения. Найти функцию распределения. Найти вероятность попадания случайной величины X на участок от а/2 до а. Найти характеристики случайной величины Х: 9.7. Известна функция распределения срока службы блока
Найти коэффициент K.Найти средний срок службы и дисперсию срока службы блока. 9.8. Плотность вероятности случайной величины Х задана функцией:
Найти ее функцию распределения, построить графики плотности вероятности и функции распределения. 9.9. Плотность распределения времени безотказной работы электронно-лучевой трубки имеет вид (по закону Вейбулла)
Найти функцию распределения случайной величины T и вероятность безотказной работы трубки в течение 4 часов. 9.10. Случайная величина X подчинена закону Симпсона ("Закону равнобедренного треугольника") на участке от -a до a.
x -a 0 a Написать выражение плотности распределения. Найти функцию распределения. Найти числовые характеристики случайной величины X: 9.11. Плотность распределения непрерывной случайной величины в интервале 9.12. Дана плотность распределения вероятностей непрерывной случайной величины
Найти функцию распределения. Построить графики функций f(x) и F(X).
|


 и показать эту вероятность на графиках плотности и функции распределения. Найти математическое ожидание и дисперсию.
и показать эту вероятность на графиках плотности и функции распределения. Найти математическое ожидание и дисперсию. f(x)
f(x) дисперсию и среднее квадрати-
дисперсию и среднее квадрати- Найти коэффициент A. Определить математическое ожидание и дисперсию случайной величины X. Найти функцию распределения и вероятность того, что значения случайной величины будут находиться в интервале (0;
Найти коэффициент A. Определить математическое ожидание и дисперсию случайной величины X. Найти функцию распределения и вероятность того, что значения случайной величины будут находиться в интервале (0;  ).
).

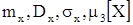 .
.



 f(x)
f(x) Найти вероятность попадания случайной величины X в интервал (-a/2; a).
Найти вероятность попадания случайной величины X в интервал (-a/2; a).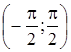 равна
равна  , вне этого интервала f(x) =0. Найти вероятность того, что в трех независимых испытаниях случайная величина X примет ровно два раза значение, заключенное в интервале (0;
, вне этого интервала f(x) =0. Найти вероятность того, что в трех независимых испытаниях случайная величина X примет ровно два раза значение, заключенное в интервале (0;  ).
).



