Задача № 8.
8.1. Найти математическое ожидание суммы очков, выпадающих на двух игральных кубиках при одном бросании. 8.2. В лотерее разыгрывается мотоцикл стоимостью 250 р., велосипед стоимостью 50 р. и часы за 40 р. Найти математическое ожидание выигрыша для лица, имеющего: а) 1 билет; б) 2 билета, если общее число билетов равно 100. 8.3. Случайная величина X - число попаданий мяча в корзину при одном броске. Вероятность попадания равна 0,3. Найти математическое ожидание этой случайной величины, дисперсию, второй начальный момент и третий центральный момент. 8.4. Производится ряд выстрелов по мишени с вероятностью попадания 0,8 при каждом выстреле, стрельба ведется до первого попадания в мишень, но не свыше четырех выстрелов. Найти закон распределения, математическое ожидание и дисперсию числа произведенных выстрелов. Построить функцию распределения, определить вероятность того, что число выстрелов до первого попадания будет не менее трех. 8.5. Дан перечень возможных значений дискретной случайной величины X: 8.6. Известно, что в партии из 20 телефонных аппаратов имеется 5 неисправных. Из партии выбрано 4 аппарата. Найти закон распределения, математическое ожидание и дисперсию числа неисправных аппаратов среди отобранных. Построить функцию распределения. Определить вероятность того, что число неисправных аппаратов среди отобранных будет не более двух. 8.7. Вероятность изготовления нестандартного изделия при налаженном технологическом процессе постоянна и равна 0,1. Для проверки качества изготовляемых изделий отдел технического контроля берет из партии не более 4-х деталей. При обнаружении нестандартного изделия вся партия задерживается. Составить закон распределения числа изделий, проверяемых из каждой партии. Найти математическое ожидание, среднее квадратическое отклонение этой случайной величины.
8.8. Случайная величина Х распределена по следующему закону:
Найти 8.9. Вероятность того, что стрелок попадает в мишень при одном выстреле, равна 0,6. Стрелку последовательно выдаются патроны до тех пор, пока не промахнется, но не более 5 патронов. Найти закон распределения, математическое ожидание и дисперсию числа выданных патронов. Построить функцию распределения. Определить вероятность того, что число выданных патронов будет не менее трех. 8.10. Испытуемый прибор состоит из трех малонадежных элементов. Отказы элементов за некоторое время Т независимы, а их вероятности равны соответственно
|

 , а также даны математические ожидания этой случайной величины и ее квадрата
, а также даны математические ожидания этой случайной величины и ее квадрата  . Найти вероятности P1, P2, P3, соответствующие возможным значениям
. Найти вероятности P1, P2, P3, соответствующие возможным значениям  .
.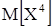 и
и 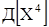 .
. Найти закон распределения, математическое ожидание числа отказавших за время Т элементов. Построить функцию распределения. Определить вероятность того, что число отказавших элементов будет не менее двух.
Найти закон распределения, математическое ожидание числа отказавших за время Т элементов. Построить функцию распределения. Определить вероятность того, что число отказавших элементов будет не менее двух.


