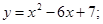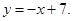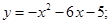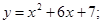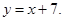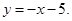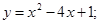Аналитическая геометрия, векторная алгебра
1-10. Даны вершины 1. А (1;1), В (7;1), С (4;5) 2. А (1;1), В (7;2), С (4;5) 3. А (1;1), В (7;3), С (4;5) 4. А (1;1), В (7;4), С (4;5) 5. А (1;1), В (7;5), С (4;5) 6. А (1;1), В (8;1), С (4;5) 7. А (1;1), В (8;2), С (4;5) 8. А (1;1), В (8;3), С (4;5) 9. А (1;1), В (8;4), С (4;5) 10. А (1;1), В (8;5), С (4;5)
11-20. Дано уравнение 1) доказать, что оно является уравнением сферы; 2) найти координаты центра и радиус сферы; 3) составить уравнение плоскости, проходящей через центр сферы и ось Oz; 4) составить уравнения прямой, проходящей через центр сферы и начало координат. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20.
21-30. Найти пределы функций.
21. 1) 2) 4) 22. 1) 2) 4) 23. 1) 2) 4) 24. 1) 2) 4) 25. 1) 2) 4) 26. 1) 2) 4) 27. 1) 2) 4) 28. 1)
2)
4) 29. 1) 2) 4) 30. 1) 2) 4)
31-40. Найти производные заданных функций.
31. а) в) 32. а) в) 33. а) в) 34. а) в) 35. а) в) 36. а) в) 37. а) в) 38. а) в) 39. а) в) 40. а) в)
41-50. Вычислить приближенное значение
41. 42. 43. 44. 45. 46. 47. 48. 49. 50.
51-60. Исследовать функцию
51.
53. 55. 57. 59.
61-70. Найти неопределенные интегралы. Результаты проверить дифференцированием.
61. а) 62. а) 63. а) 64. а) 65. а) 66. а) 67. а) 68. а) 69. а) 70. а) 71-80. Вычислить по формуле Ньютона-Лейбница определенный интеграл
71. 74. 77. 80.
81-90. Вычислить площадь фигуры, ограниченной параболой
81. 82. 83. 84. 85. 86. 87. 88. 89. 90.
|



 треугольника. Найти: 1) длину стороны AB; 2) внутренний угол A в радианах с точностью до 0,01%; 3) уравнение высоты, проведенной через вершину C; 4) уравнение медианы, проведенной через вершину С; 5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины С; 7) систему линейных неравенств, определяющую внутреннюю область треугольника. Сделать чертеж.
треугольника. Найти: 1) длину стороны AB; 2) внутренний угол A в радианах с точностью до 0,01%; 3) уравнение высоты, проведенной через вершину C; 4) уравнение медианы, проведенной через вершину С; 5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины С; 7) систему линейных неравенств, определяющую внутреннюю область треугольника. Сделать чертеж. . Требуется:
. Требуется:


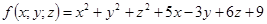

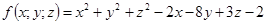




 при a)
при a) 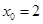 , b)
, b) 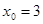 , c)
, c)  ;
; 3)
3)  ;
;
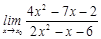 при a)
при a)  , b)
, b) 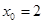 , c)
, c)  3)
3) 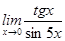 ;
;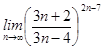
 при a)
при a)  , b)
, b) 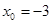 , c)
, c)  3)
3) 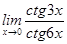 ;
;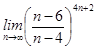
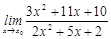 при a)
при a)  , b)
, b) 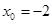 , c)
, c) 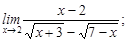 3)
3)  ;
;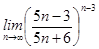
 при a)
при a)  , c)
, c)  3)
3)  ;
;
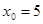 , c)
, c)  3)
3)  ;
;

 при a)
при a)  , b)
, b)  , c)
, c) 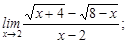 3)
3)  ;
;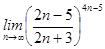
 при a)
при a)  , b)
, b)  , c)
, c) 


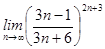
 при a)
при a)  , b)
, b)  , c)
, c)  3)
3) 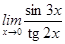 ;
;
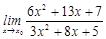 при a)
при a)  , c)
, c)  3)
3)  ;
;
 ; б)
; б) 
 г)
г) 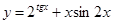 .
.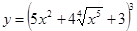 ; б)
; б) 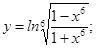
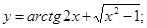 г)
г)  .
. ; б)
; б) 
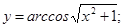 г)
г)  .
.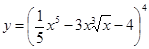 ; б)
; б) 
 г)
г) 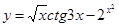 .
. ; б)
; б) 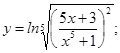
 г)
г) 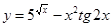 .
. ; б)
; б) 
 г)
г) 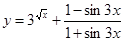 .
.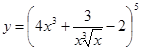 ; б)
; б) 
 г)
г)  .
. ; б)
; б) 
 г)
г) 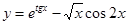 .
.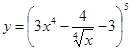 ; б)
; б) 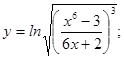
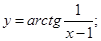 г)
г) 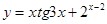 .
. ; б)
; б) 
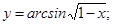 г)
г)  .
.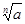 , заменив в точке
, заменив в точке  приращение функции
приращение функции 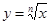 дифференциалом.
дифференциалом.
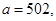




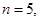



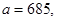



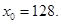
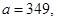

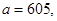
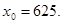
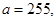
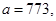
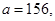
 и построить ее график.
и построить ее график. 52.
52. 
 54.
54. 
 56.
56. 
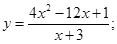 58.
58. 
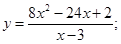 60.
60. 
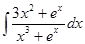 ; б)
; б)  ;
; ; б)
; б) 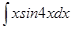 ;
;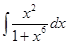 ; б)
; б)  ;
; ; б)
; б) 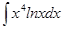 ;
; ; б)
; б)  ;
;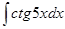 ; б)
; б) 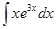 ;
; ; б)
; б) 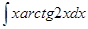 ;
;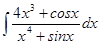 ; б)
; б) 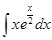 ;
;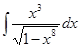 ; б)
; б)  ;
; ; б)
; б) 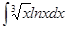 .
.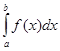 .
. 72.
72. 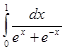 73.
73. 
 75.
75. 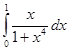 76.
76. 
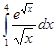 78.
78.  79.
79. 

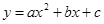 и прямой
и прямой 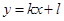 . Сделать чертеж.
. Сделать чертеж.