ДИСКРЕТНАЯ МАТЕМАТИКА
КОНТРОЛЬНАЯ РАБОТА ПО ДИСЦИПЛИНЕ
для студентов специальностей Организация и технология защиты информации Программное обеспечение ВТ и АC Вычислительные машины, сети и телекоммуникации Тема. Основные понятия комбинаторики Комбинаторика – раздел математики, посвященный решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения некоторой конструкции из элементов исходного множества. Поэтому задачу комбинаторики можно определить как изучение разнообразных свойств конфигураций, построенных из элементов данного множества. Простейшими примерами комбинаторных конфигураций являются перестановки, размещение, сочетания и разбиение. При подсчете комбинаторных конфигураций используются правила суммы и произведения. Правило суммы. Если объект А может быть выбран m способами, а объект В другими n способами, то выбор “либо А, либо В” может быть осуществлен m+n способами. Правило произведения. Если объект А может быть выбран m способами и после каждого из таких выборов объект В в свою очередь может быть выбран n способами, то выбор “A и B” в указанном порядке может быть осуществлен mn способами. Правила эти по своей природе являются определениями, и их нужно скорее понимать, нежели доказывать. Следует заметить, что в первом правиле выборы А и В являются взаимно исключающими, т.е. нет возможности выбрать оба объекта одновременно (одним и тем же путем). Правило произведения наиболее часто используется в тех случаях, когда порядок выбора не является существенным, т.е. когда выборы А и В оказываются независимыми. Не следует, однако, игнорировать возможность наличия такой зависимости. Перестановками из n элементов называются соединения, каждое из которых содержит n элементов и которые отличаются между собой лишь порядком расположения элементов. Число
где n! – читается “n факториал” (от латинского factor – множитель). Пример: Рассмотрим перестановку из трех чисел: 1, 2, 3. Из этих трех чисел можно составить всего 3! = 6 перестановок: 123, 132, 321, 312, 231, 213. В первой перестановке все числа идут в натуральном порядке, а в остальных перестановках этот порядок нарушен. Например, в перестановке 312 число 3 стоит и впереди 1 и впереди 2. Такое явление, когда большее число находится впереди меньшего, называется беспорядком или инверсией. В частности, в перестановке 132 наблюдается одна инверсия, в 312 – две инверсии, а в 321 – три инверсии и т.д. Пример:Подсчитать число инверсий в перестановке 531642. Решение: Начинаем с подсчета чисел, стоящих впереди 1 – их два (5 и 3). Зачеркиваем 1. Впереди 2 стоят четыре числа (5, 3, 6 и 4). Зачеркиваем 2. Впереди 3 стоит одно число (5). Зачеркиваем 3. Впереди 4 стоят два числа (5, 6). Зачеркиваем 4. Впереди 5 ничего не стоит. Зачеркиваем 5. Наконец, впереди 6 также ничего не стоит (все вычеркнуть). Следовательно, искомое число инверсией равно 2+4+1+2=9. Операция перемещения двух элементов в данной перестановке называется транспозицией. Все перестановке из n чисел 1, 2, 3, …, n можно разбить на два класса. Перестановку называют четной (или четного класса), если число ее инверсий четное, и нечетной (нечетного класса) в противном случае. Например, перестановка 231 является четной, так как она имеет две инверсии. Но если применить к ней транспозицию (2, 3), то получим перестановку 321 с тремя инверсиями, т.е. нечетную перестановку. Теорема:От одной транспозиции четность перестановки меняется. Из теоремы следует. 1. Чтобы перейти от одной перестановки к другой того же класса, надо выполнить четное число транспозиций. Напротив, чтобы перейти от одной перестановки к другой противоположного класса, надо выполнить нечетное число транспозиций. 2. Из n чисел 1, 2, …, n можно составить Подстановкой из n элементов
называется замена каждого элемента Обычно подстановку обозначают символом
Если рассматривать только номера элементов, то запись подстановки (2) упрощается
Очевидно, что различные подстановки из n чисел должны иметь в нижней строке запись (3) различные перестановки. Отсюда следует, что число подстановок n – й степени (т.е. подстановок из n чисел) равно числу перестановок из n чисел, т.е. равно n!. Подстановку n – й степени называют четной, если нижняя строка ее записи (3) образует четную перестановку, и нечетной, если эта строчка образует нечетную перестановку. Как определить четность подстановки n – й степени, если она записана в виде
Пусть Можно показать, что подстановка S является четной, когда Пусть даны две подстановки чисел 1, 2, 3, 4
Посмотрим что произойдет, если сначала выполнить подстановку Подстановка
Которая одна производит то же действие, это обе подстановки Произведением подстановок S и T из n чисел 1, 2, …, n называют такую третью подстановку из тех же чисел, которая одна производит то же действие, что обе подстановки S и T, произведенные последовательно одна за другой. Произведение подстановок обозначают так = ST. Можно показать, что не всегда ST = TS. Например
но
Среди всевозможных подстановок чисел 1, 2, …, n имеется одна, так называемая тождественная или единичная подстановка
которая при умножении подстановок ведет себя аналогично числу 1 при арифметическом умножении, а именно: для любой подстановки
имеет место равенство SJ = JS = S. Для каждой подстановки S всегда существует обратная подстановка S где Умножение подстановок из 1, 2, …, n, подчиняется сочетательному закону (ST) U = S (TU). Подстановку S из чисел 1, 2, …, n называют k – членной циклической или k – членным циклом, если она Циклическая подстановка обычно обозначается символом ( Например
есть четырехмерная циклическая подстановка (1 2 3 4). Транспозиция (ij) есть двучленная циклическая подстановка. Запись цикла можно начинать с любого числа, входящего в его состав. Например, подстановку (3 1 2 5) из n чисел 1, 2, …, n можно записать в виде (1 2 5 3) или в виде (5 3 2 1) и т.д. Всякую подстановку из чисел 1, 2, …, n можно представить как произведение независимых циклов. Независимых в том смысле, что никакие два цикла разложения не имеют общих чисел. Рассмотрим подстановку
Подстановка (*) число 1 переводит в 3, число 3 – в 5, число 5 – в 7 и 7 – в исходное число 1. Т.е., получается цикл (1 3 5 7). Однако в цикл (1 3 5 7) вошли не все числа подстановки (**), например число 2. Поэтому начнем новый цикл с этого числа (или с какого – нибудь другого числа, не вошедшего в первый цикл). Подстановка (**) число 2 переводит в 4, 4 – в 6, 6 – в 8, 8 – в 2. Получился цикл (2 4 6 8) и все числа подстановки (*) исчерпаны. Итак,
Рассмотрим еще один пример. Разложим на независимые циклы подстановку
Здесь 1 переводится в 4, 4 – в 2 и 2 – в 1. Получился цикл (1 4 2). Но в этот цикл не вошло число 3. Число 3 переводится в 3. Записываем это так: (3). Получился одночленный цикл и
Впрочем, цикл (3) можно опустить, так как он является тождественной подстановкой. Тогда разложение примет более простой вид
Очевидно, что этот способ разложения на произведение циклов применим к любой подстановке. В силу независимости циклов порядок их следования может быть произвольным. В свою очередь всякий цикл можно представить в виде произведения транспозиций, но такое произведение уже не будет разложением на независимые циклы. Таким образом, порядок следования транспозиций имеет уже существенное значение. Например, цикл (2 3 5 6) можно разложить следующим образом на транспозиции (2 3 5 6) = (2 3)(2 5)(2 6). Действительно, первая транспозиция (2 3) переводит 2 в 3, а остальные транспозиции (2 5) и (2 6) число 3 не изменяются. Следовательно, произведение (2 3) (2 5)(2 6) число 2 переводит в 3. Затем число 3 транспозицией (2 5) переводится в 5, а 5 транспозицией (2 6) не изменяется. Значит, произведение (2 3) (2 5)(2 6) число 3 переводит в 5. Далее, число 5 транспозицией (2 5) переводится в 2, после чего 2 транспозицией (2 6 0 переводится в 6. Т.о., произведение (2 3)(2 5) (2 6) число 5 переводит в 6. Наконец, (2 3) и (2 5) число 6 не изменяют, а (2 6) число 6 переводит в 2. Поэтому, (2 3) и (2 5) число 6 не изменяют, а (2 6) число 6 переводит в 2. Поэтому (2 3)(2 5)(2 6) переводит 6 в исходное число 2. Отсюда получается, что (2 3)(2 5)(2 6) = (2 3 5 6). Рассуждая таким образом можно убедится, что всякий k – членный цикл
Теорема:Всякую подстановку из n чисел 1, 2, …, n можно разложить на n – S транспозиций, где S – число независимых циклов (включая и одночленные), на которые разлагается данная подстановка. Разность n – S называется декрементом подстановки и обладает следующим свойством. Теорема:Если p – число инверсий в перестановке имеет ту же четность, что и число p. Иными словами, четность подстановки S и ее декремент совпадают. Для примера рассмотрим подстановку
Найдем декремент подстановки, для чего разложим ее на независимые циклы S = (6 1 3)(5 2)(4). Таким образом S = 3, а декремент n –S = 6 – 3 = 3 есть нечетное число. Размещениями из n элементов по m Число размещений из n элементов по m обозначается символом Число все возможных размещений из n элементов по m равно произведению m последовательных чисел натурального ряда, наибольший из которых есть n, т.е.
или
Например, Сочетаниями из n элементов по m Число различных сочетаний из n элементов по m обозначается символом Наряду с Число всевозможных сочетаний из n элементов по m равно частному от деления произведения последовательных чисел натурального ряда, наибольшее из которых равно n, на произведение последовательных натуральных чисел от 1 до m включительно, т.е.
Формулу (7) можно выразить через число перестановок (1) и число размещений (5).
или
Например:
= Замечание 1. По определению сочетаний символов Замечание 2.Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Например, если среди n элементов есть элементов одного типа, элементов другого вида и т.д., то число перестановок с повторениями
где Число размещений с повторением равно
Например, из цифр 1, 2, 3, 4 можно составить
трехзначных чисел. Число сочетаний с повторениями из n элементов по m обозначается через
Например, число различных бросаний двух одинаковых кубиков равно
Бином Ньютона или, точнее, формула бинома Ньютона используется при решении многих задач. Бином в переводе на русский язык означает двучлен. Рассмотрим правило возведения в целую натуральную степень n бинома a + b. Пусть n = 1, тогда
При n = 2 имеет
При n = 3
При n = 4
Используя число сочетаний, (9) можно представить в виде
Формула (10) называется формулой бином Ньютона, а правая часть ее называется разложением бинома. Выражение (10) можно записать и так
Числа Например,
1. Количество членов разложения бинома на единицу больше показателя степени бинома. 2. Все члены разложения имеют одну и ту же степень n относительно первого и второго членов бинома, то есть разложение есть однородный многочлен, причем показатели первого члена убывают от n до 0, а второго возрастают от 0 до n. 3. Коэффициенты разложения следуют так: первый равен 1 = 4. Общий член разложения вычисляется по формуле
5. Биноминальные коэффициенты, равноотстоящие от концов разложения, равны между собой, то есть
6. Из свойств (1) и (5) следует, что если показатель бинома четный, то в разложении средний член имеет наибольший биноминальный коэффициент, а если нечетный – то имеется два средних члена с одинаковым наибольшим коэффициентом. 7. Сумма всех биноминальных коэффициентов равна Если в формуле (10) положить a = b = 1, то получим
8. Сумма биноминальных коэффициентов, стоящих на четных местах, равна сумме коэффициентов, стоящих на нечетных местах. Для вычисления биноминальных коэффициентов удобно пользоваться так называемым треугольником Паскаля, который выглядит так
Заметим, что треугольник Паскаля можно представить и в виде таблицы
|

 всех перестановок из n элементов равно произведению последовательных натуральных чисел от 1 до n включительно, т.е.
всех перестановок из n элементов равно произведению последовательных натуральных чисел от 1 до n включительно, т.е. (1)
(1)
 четных перестановок и столько же нечетных.
четных перестановок и столько же нечетных. (*)
(*) произвольной перестановки элементов (*) вполне определенным элементом
произвольной перестановки элементов (*) вполне определенным элементом  (2)
(2) (3)
(3) (4)
(4) , где S – число инверсий в верхней строке и t – число инверсий в нижней строке записи (4) подстановки S.
, где S – число инверсий в верхней строке и t – число инверсий в нижней строке записи (4) подстановки S. - четное число, и нечетной, когда
- четное число, и нечетной, когда 
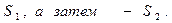
 заменяет 1 на 4, а
заменяет 1 на 4, а  - 4 на 3. Т. о., число 1 под влиянием двух подстановок
- 4 на 3. Т. о., число 1 под влиянием двух подстановок 
 ,
,
 ,
,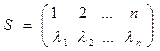
 , характеризующая равенством
, характеризующая равенством .
. переводит в число
переводит в число  , отличное от
, отличное от  , отличное от
, отличное от  - в число
- в число  , отличное от
, отличное от  u), а прочие числа (k < u) оставляет неизменными.
u), а прочие числа (k < u) оставляет неизменными.
 (**)
(**)



 разлагается на такое произведение k – 1 транспозиций
разлагается на такое произведение k – 1 транспозиций
 из чисел 1, 2, …, n, то декремент подстановки
из чисел 1, 2, …, n, то декремент подстановки  .
. называются соединения, в каждое из которых входит m элементов, взятых из данных n элементов, и которые отличаются между собой элементами (хотя бы одним) или их порядком.
называются соединения, в каждое из которых входит m элементов, взятых из данных n элементов, и которые отличаются между собой элементами (хотя бы одним) или их порядком. (от французского слова Arramgement - размещение).
(от французского слова Arramgement - размещение). (5)
(5)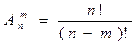 (6)
(6)
 называются соединения, в каждое из которых входят m элементов, взятых из данных n элементов и которые отличаются только элементами (хотя бы одним).
называются соединения, в каждое из которых входят m элементов, взятых из данных n элементов и которые отличаются только элементами (хотя бы одним). (от латинского Combinare – соединить).
(от латинского Combinare – соединить). употребляют такие обозначения
употребляют такие обозначения  .
.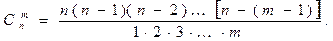 (7)
(7)
 . (8)
. (8)

 не имеет смысла. Но в целях единообразной формы записи по определению принимают
не имеет смысла. Но в целях единообразной формы записи по определению принимают 
 +
+  +….=
+….= 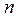 .
.

 и выражается по формуле
и выражается по формуле .
.



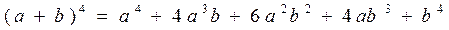 Нетрудно показать, что для произвольного натурального n имеет место формула
Нетрудно показать, что для произвольного натурального n имеет место формула

 (9).
(9).
 (10)
(10) (11)
(11)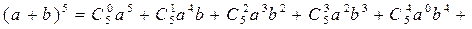
 Свойства разложения бинома Ньютона
Свойства разложения бинома Ньютона ,
,  ,
,  , …,
, …,  , то есть коэффициент (k+1)–го члена равен
, то есть коэффициент (k+1)–го члена равен  . Эти коэффициенты, называемые биноминальными, всегда натуральные числа, если показатель бинома натуральное число.
. Эти коэффициенты, называемые биноминальными, всегда натуральные числа, если показатель бинома натуральное число.
 ,
,  ,
,  , …,
, …,  .
. , где n – показатель бинома.
, где n – показатель бинома.


