Контрольная работа. Методы координат на плоскости

 

1. Методы координат на плоскости.
2. Основные задачи, решаемые методом координат.
3. Уравнение прямой с угловым коэффициентом.
4. Общее уравнение прямой.
5. Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом.
6. Уравнение прямой, проходящей через две данные точки.
7. Уравнение прямой в отрезках.
8. Угол между двумя прямыми.
9. Взаимное расположение двух прямых на плоскости.
10. Расстояние от точки до прямой.
11. Уравнение окружности.
12. Каноническое уравнение эллипса.
13. Каноническое уравнение гиперболы.
14. Директрисы эллипса и гиперболы.
15. Каноническое уравнение параболы.
16. Матрица. Виды матриц.
17. Операции над матрицами.
18. Определители квадратных матриц.
19. Миноры, алгебраические дополнения, теорема Лапласа.
20. Обратная матрица. Алгоритм вычисления обратной матрицы.
21. Ранг матрицы.
22. Решение системы линейных уравнений (СЛАУ) по формулам Крамера.
23. Решение СЛАУ методом обратной матрицы.
24. Решение СЛАУ методом Гаусса.
25. Теорема Кронекера – Капелли.
26. Дать основные понятия вектора.
27. Линейные операции над векторами.
28. Понятие линейной зависимости векторов.
29. Линейная зависимость векторов на плоскости.
30. Линейная зависимость векторов в пространстве.
31. Базис на плоскости и в пространстве.
32. Скалярное произведение векторов и его основные свойства.
33. Направляющие косинусы вектора.
34. Векторное произведение векторов и его основные свойства.
35. Смешанное произведение векторов и его основные свойства.
36. Плоскость. Уравнение плоскости, проходящей через данную точку перпендикулярно к данному вектору.
37. Неполное уравнение плоскости.
38. Уравнение плоскости в отрезках.
39. Расстояние от точки до плоскости.
40. Угол между плоскостями.
41. Условия параллельности и перпендикулярности плоскостей.
42. Общее уравнение прямой в пространстве.
43. Каноническое уравнение прямой в пространстве.
44. Параметрические уравнения прямой.
45. Уравнение прямой в пространстве, проходящее через две различные данные точки.
46. Угол между прямыми в пространстве.
47. Условия параллельности и перпендикулярности прямой и плоскости.
48. Уравнение плоскости, проходящей через данную точку и параллельной данной плоскости.
49. Уравнение плоскости, проходящей через две данные точки перпендикулярной к данной плоскости.
50. Уравнение плоскости, проходящей через три данные точки не лежащие на одной прямой.

 

 

 

 

Контрольная работа

Вариант 1

1. Вычислите определенные интегралы:
   а) ; б) ;
2. Найдите площадь фигуры, ограниченной линиями:
   а) и ; б) , , ;
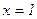3. Вычислите несобственный интеграл (или установите его расходимость): .
4. Найдите общие решения уравнений:
   а) ; б) ; в) ;
5. Найдите решение задачи Коши: .
6. Найдите общее решение уравнения .
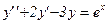7. Определите вид частного решения уравнения (коэффициентов не находите):
   .

 

Контрольная работа

Вариант 2

1. Вычислите определенные интегралы:
а) ; б) ;

2. Найдите площадь фигуры, ограниченной линиями:
а) и ; б) и ;

1. Вычислите несобственный интеграл (или установите его расходимость):
2. Найдите общие решения уравнений:
   а) ; б) в) .
3. Найдите решение задачи Коши: .
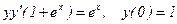4. Найдите общее решение уравнения .
5. Определите вид частного решения уравнения (коэффициентов не находите):
   .