Методические указания по выполнению задач № 1–2
Приступая к выполнению данной задачи, студент должен изучить вопросы спектрального анализа сигналов, твердо усвоить и отчетливо представлять, что такое амплитудный и фазовый спектры сигнала, их физический смысл и практическое значение, овладеть приемами расчета, включая способы раскрытия неопределенностей, особенностью расчета спектра сигналов, описываемых четными и нечетными функциями и т. д. С целью облегчения работы студенту вместе со списком литературы ниже даются краткое введение в спектральный анализ и примеры расчета, показывающие целесообразную последовательность изучения материала и рассматривающие наиболее сложные моменты определения спектра сигналов. Как известно из курса высшей математики, любая периодическая функция f(t) с периодом Т, удовлетворяющая условиям Дирихле, может быть разложена в интервале (О, Т) или (-Т/2; Т/2) в ряд Фурье:
где а0, аn, bn – коэффициенты ряда Фурье, которые вычисляются по следующим формулам:
где Для практических целей удобно объединить косинусоидальные и синусоидальные колебания одинаковой частоты в одно колебание:
где
С учетом (5) ряд (1) может быть записан в виде
Колебание вида А(t) = Ansin(nwt+j) называется гармоническим, поэтому ряд Фурье также называют гармоническим. Совокупность гармоник ряда (7), представляющего функцию f(t), называют ее спектром или чаще – спектром сигнала, который описывается данной функцией. Различают амплитудный спектр (совокупность амплитуд Аn) и фазовый спектр (совокупность начальных фаз jn). Расчет амплитудного и фазового спектров может быть выполнен по формулам (2), (3), (4) и (6). Следует иметь в виду, что при расчете может иметь место неопределенность при некоторых значениях n. Порядок расчета с раскрытием неопределенности показан в примере. Ниже поясняется порядок расчета амплитудного и фазового спектров на примере прямоугольного импульса постоянного тока.
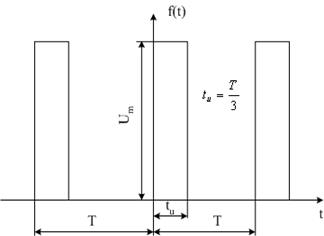
Первый пример решения задачи Требуется найти аналитическое выражение и построить амплитудный и фазовый спектры сигнала, показанного на рис. 1а. Для этого необходимо разложить в ряд Фурье в интервале (О,Т) функцию f(t), описывающую данный сигнал. В соответствии с общим правилом по формулам (2)–(4) вычисляем коэффициенты ряда:
Интеграл берем в интервале от 0 до tu, т. к. f(t)=0 на отрезке от tu и до Т и, следовательно,
а) б)
в)
Рис. 1. Графики: а – исходной функции; б – амплитудно-частотного спектра; в – фазочастотного спектра
Для нахождения амплитудного спектра сигнала необходимо вычислить амплитуду An каждой гармонической составляющей сигнала, определяемой суммой двух колебаний одной частоты, но сдвинутых друг относительно друга на 90 °, а именно
Подставив значения
Найденные по этой формуле значения An могут получиться отрицательными. Для расчета амплитудного спектра следует использовать абсолютные значения An. Графически спектр изображается в системе координат X, Y, где по оси X откладываются номера гармоник n (или их частоты nw), а по оси Y – соответствующие им амплитуды An (рис. 1б). Фазовый спектр определяется аналогично амплитудному. В соответствии с формулой (6) имеем
Подставив значения tu и w, получим
Поскольку jn является аргументом функции тангенса, имеющей период p, то к jn можно прибавить или от jn отнять любое целое число p. Поскольку в данном случае jn возрастает в области отрицательных значений с увеличением n, то удобнее прибавлять целое число p. Таким образом, окончательно можно записать:
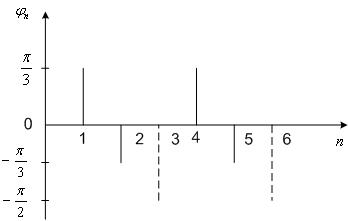
Графически фазовый спектр изображен на рис. 1в, причем значения jn для n, кратных трем, показаны пунктиром, поскольку Аn = 0 для этих значений n. Это можно истолковать так: гармоники, номера которых кратны трем, имеют начальную фазу - Расчет может быть значительно сокращен и упрощен, если использовать свойства функции f (t). Известно, что если f (t) – четная, т. е. f (t) = f (- t), то ее разложение в ряд Фурье не содержит членов с синусами, а если f (t) – нечетная, т. е.
а для нечетной f (t): Кроме того, выражения для аn и bn в этом случае также упрощаются. Для четной f (t):
где bn = 0, Аn = аn; а для нечетной:
Таким образом, для четных f (t) необходимо вычислять только а0 и аn, а для нечетных – только bn. Второй пример решения задачи Требуется найти аналитическое выражение амплитудного спектра сигнала, показанного на рис. 2а. Сигнал описывается выражением:
и существует в интервале от -
а)
б)
Рис. 2. Графики: а – амплитудный спектр; б – полученная функция
Далее введем обозначения:
Тогда выражение для bn запишется так:
Подставив в полученное выражение значения
При В таких случаях значения коэффициентов ряда Фурье находят по формулам (3), (4) путем подстановки в них данной конкретной величины n. В нашем примере в выражение (4) подставляем
Подставив
а при n = 3: Амплитудный спектр изображен на рис. 2б. Фазовый спектр данного сигнала можно специально не показывать на рисунке, т. к. гармоники с нулевой амплитудой имеют нулевую начальную фазу. Это следует из факта, что аn = 0 для всех значений n. Для тех же значений n, при которых bn = 0, определять начальную фазу нет необходимости. При определении спектра частот сигнала DFc (рис. 1б) следует учесть составляющие спектра от нулевой (n = 0) до второй гармоники (n = 2), т. е. D n = 2. Тогда Зная длительность элементарного импульса tu, можно вычислить DFc.
|

 ,
,
 ,
,
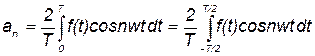 ,
,
 ,
,
 – круговая частота.
– круговая частота.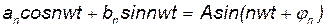 ,
,
 ,
,  .
.
 .
.
 .
. . Аналогично вычисляются коэффициенты an и bn:
. Аналогично вычисляются коэффициенты an и bn:

 ;
;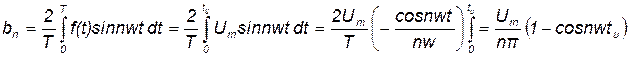 .
.

 :
:
 и
и  в найденное выше выражение, получим
в найденное выше выражение, получим ;
;  .
. .
. .
. ; k = 0, 1, 2, 3,…
; k = 0, 1, 2, 3,…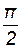 (или + p/2) и амплитуду, равную нулю.
(или + p/2) и амплитуду, равную нулю. и членов с косинусами. Таким образом, ряд Фурье запишется для четной f (t):
и членов с косинусами. Таким образом, ряд Фурье запишется для четной f (t):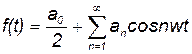 ,
, .
. ,
,

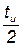 до
до 

 ,
,  .
.

 и
и  , произведя несложные преобразования, получим расчетную формулу для bn:
, произведя несложные преобразования, получим расчетную формулу для bn: .
. , т. е. nw = w0, имеет место неопределенность вида
, т. е. nw = w0, имеет место неопределенность вида  .
. :
:
 , получаем расчетную формулу:
, получаем расчетную формулу: 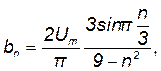
 .
.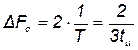 .
.


