Линейная алгебра с элементами аналитической геометрии
1 - 10. В декартовой прямоугольной системе координат даны координаты вершин пирамиды ABCD. Постройте чертеж и решите следующие задачи: а) докажите, что система векторов б) постройте вектор в) найдите длину ребра AB; г) вычислите величину угла между ребрами AB и AC; д) напишите уравнение прямой АВ; е) составьте уравнение плоскости АВС; ж) напишите уравнение высоты, опущенной из вершины D на плоскость АВС.
1. A(1,-1,0), B(2,3,1), C(-1,1,1), D(4,-3,5). 2. A(2,0,-1), B(1,1,1), C(4,6,6), D(-1,2,3). 3. A(-3,1,1), B(0,-4,-1), C(5,1,3), D(4,6,-2). 4. A(1,1,4), B(2,1,2), C(1,-1,2), D(6,-3,8). 5. A(2,1,-4), B(-3,-5,6), C(0,-3,-1), D(-5,2,-8). 6. A(3,0,1), B(1,3,0), C(4,-1,2), D(-4,3,5). 7. A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). 8. A(2,-2,1), B(1,2,-1), C(1,0,2), D(2,1,0). 9. A(1,-1,1), B(2,1,-1), C(-2,0,3), D(2,-2,-4). 10. A(0,1,-1), B(-3,0,1), C(1,2,0), D(1,-1,2).
11 – 20. При выполнении плана товарооборота магазин должен продать товары трех видов в количествах а11, а12, а13 (тыс. штук) соответственно. Если продавать эти товары в количествах а21, а22, а23 (тыс. штук) соответственно, то план товарооборота будет перевыполнен в полтора раза. Если же товары продать в количествах а31, а32, а33 (тыс. штук) соответственно, то выполнение плана составит лишь 75%. Постройте математическую модель задачи и определите стоимость единицы товара каждого вида, если план товарооборота составляет Q тыс. руб. Решите задачу: а) методом Крамера; б) методом Гаусса; в) методом с использованием обратной матрицы. План товарооборота магазина Q (тыс. руб.) и значения аij (в виде матрицы) даны ниже. 11. Q = 16,
12. Q = 18,
13. Q = 20,
14. Q = 24,
15. Q = 80,
|

 линейно независима;
линейно независима;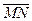 , где M и N - середины ребер AD и BC соответственно, найдите его координаты и его разложение по базису
, где M и N - середины ребер AD и BC соответственно, найдите его координаты и его разложение по базису  ;
;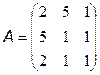 ; 16. Q = 28,
; 16. Q = 28,  ;
; ; 17. Q = 36,
; 17. Q = 36,  ;
; ; 18. Q = 42,
; 18. Q = 42,  ; 19. Q = 32,
; 19. Q = 32,  ;
; ; 20. Q = 12,
; 20. Q = 12,  .
.


