Замечание. Равносильность и означает, что уравнение однозначно определяет в рассматриваемой области дифференцируемую функцию такую, что , вообще, при .
[1] Эскрима – филлипинское боевое искусство [2] бастон - палка [3] ларго мано янток – длинная палка из ротанга. [4] Визор - ветрозащитные экраны мотоциклетного шлема [5] Дебби Даунер - персонаж культового американского шоу Saturday Night Live (Субботним Вечером в Прямом Эфире), в исполнении Rachel Dratch, наводящий на всех тоску своими замечаниями и высказываниями. Билет 26. Неявная функция. Термин «неявная функция» относится к способу задания функциональной зависимости между Следует отметить, что уравнение Кроме того, уравнение В этом примере можно например дополнительно потребовать чтобы выполнялось неравенство В общей ситуации условия, при которых существует единственная функция Теорема. Пусть определена и непрерывна вместе с частными производными и в окрестности точки такой, что и. Тогда существуют числа и такие, что на множестве уравнение равносильно уравнению где непрерывная и дифференцируемая на функция, и. Замечание. Равносильность и означает, что уравнение однозначно определяет в рассматриваемой области дифференцируемую функцию такую, что, вообще, при. Доказательство. По условию Следовательно,
Окрестность, где
Значит, можно выбрать
При любом фиксированном Таким образом, искомая функция построена. При этом, просто по построению Докажем, что Так как по построению окрестности
Из равенства (3) следует, что Аналогичными рассуждениями можно доказать такую теорему: Теорема. Пусть функция непрерывна и имеет все непрерывные частные производные в окрестности точки такой, что, причем. Тогда существуют числа такие, что в области, уравнение равносильно уравнению, причем функция непрерывна и имеет непрерывные частные производные, причем .
|

 и
и  и означает, что вместо явной формулы
и означает, что вместо явной формулы  эта зависимость представлена уравнением
эта зависимость представлена уравнением  .
. не всегда определяет функцию
не всегда определяет функцию  функцию
функцию  , задающее окружность на плоскости, определяет при
, задающее окружность на плоскости, определяет при  две непрерывные функции
две непрерывные функции  и
и  .
. . Тогда мы получим только
. Тогда мы получим только 

 . Пусть, для определенности,
. Пусть, для определенности,  . Ввиду непрерывности
. Ввиду непрерывности  из некоторой окрестности точки
из некоторой окрестности точки  такое, что функция
такое, что функция  обладает на отрезке
обладает на отрезке  положительной производной и, значит, возрастает. Поскольку
положительной производной и, значит, возрастает. Поскольку  , из этого следует, что при
, из этого следует, что при  функция
функция  , а при
, а при 
 .
.


 Далее,
Далее,  - также непрерывна. Поэтому она сохраняет знак в некоторой окрестности любой точки, где она положительна или отрицательна.
- также непрерывна. Поэтому она сохраняет знак в некоторой окрестности любой точки, где она положительна или отрицательна. так, чтобы
так, чтобы

 функция
функция  возрастает на
возрастает на  . При этом
. При этом  . Поэтому существует, притом единственное значение
. Поэтому существует, притом единственное значение  такое, что
такое, что  . Это значение соответствует точке
. Это значение соответствует точке  . Это соответствие и обозначается
. Это соответствие и обозначается  .
. при
при  .
. непрерывна. Пусть приращению
непрерывна. Пусть приращению  соответствует приращение
соответствует приращение  . При этом
. При этом 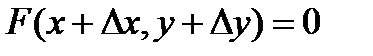 по построению
по построению  . Но
. Но  - дифференцируемая функция, поэтому
- дифференцируемая функция, поэтому  (3), где
(3), где  при
при  .
. , из равенства (3) следует, что при
, из равенства (3) следует, что при  также и
также и  , что означает непрерывность построенной
, что означает непрерывность построенной  .
. .
. , т.к.
, т.к.  ,
,  и
и 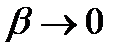 при достаточно малых
при достаточно малых  (а значит, по доказанному выше, и
(а значит, по доказанному выше, и  ) коэффициент при
) коэффициент при  отличен от
отличен от  и
и  . Значит,
. Значит,  . Теорема доказана.
. Теорема доказана.


