Уравнивание одиночного нивелирного хода

 

№ секции	№ марок и реперов	Длины секций L, км	Превышения	Расхождения	d2	d2 L	Поправки n, мм	Исправленные превышения h+n, м	Отметки H, м	Вес отметки PH	Ср. кв. ошибка МH, мм	Ср. кв. ошибка самой ошибки mМH, мм
Прямой ход h, м	Обратный ход h, м	Среднее h, м	Полученные d, мм	Предельно допустимые, мм
	М25	3,1	+3,617	-3,627	+3,622	-10				+4	+3,626	151,635
	Рп11	155,261	0,39	4,2	1,31
4,2	+5,169	-5,178	+5,174	-9				+6	+5,180
	Рп12	160,441	0,22	5,5	1,75
3,9	-5,343	+5,349	-5,346	+6				+5	-5,341
	Рп13	155,100	0,22	5,5	1,75
1,7	+9,659	-9,663	+9,661	-4				+3	+9,664
	Рп14	164,764	0,25	5,2	1,64
5,9	-8,246	+8,265	-8,256	+19				+8	-8,246
	М27	156,516
18,8	+4,856	-4,854	+4,855					+26

Н_К – Н_Н = +4,881

f_h = -0,026 м контроль

f_{h пред.} = 0,043 м

Данные для решения задачи

Рис. 4.

 

В графы 1, 2, 3, 4 и 5 выписывают исходные данные и измеренные величины со схематического чертежа (рис. 4). Дальнейшие вычисления выполняют в следующей последовательности:

1. В графе 6 вычисляют средние превышения по секциям. Знак берут по прямому ходу, а величину – как среднее арифметическое из абсолютных значений h_пр и h_обр.

 

(1)

 

2. Контроль вычислений средних превышений выполняют суммированием величин, записанных в графы 4, 5 и 6 по формуле

 

(2)

 

3. В графе 7 вычисляют расхождения d_i (в мм) между превышениями прямого и обратного ходов

 

(3)

 

4. Полученные разности сравнивают с предельными значениями (графа 8), найденными по формуле

 

(4)

 

где L_i – длина секции в км.

5. Для оценки точности полевых измерений в графах 9 и 10 вычисляют величины d² и d²/L, причём величины d берут в мм, а L – в км. После этого вычисляют среднюю квадратическую ошибку среднего превышения на 1 км хода по формулам:

 

(5)

 

где d – разность между h_пр и h_обр в секции, мм;

L – длина секции, км;

[L] – длина хода, км.

6. Ошибка самой ошибки характеризует точность получения величины m_км, вычисляемой по формуле

 

(6)

 

7. Посчитывают невязку по ходу

 

(7)

 

где

Н_кон и Н_нач – отметки конечной и начальной марок или реперов.

8. Полученную невязку по формуле 7 сравнивают с предельной невязкой нивелирного хода

 

(8)

 

где L – длина хода в км.

9. Делают вывод о качестве (точности) полевых измерений. Если:

- d_i £ d_пред;

- m_км £ 5 мм (допуск по инструкции для III кл.);

- f_h £ f_{h доп},

то измеренные превышения по точности соответствуют III классу. В противном случае превышения перемеряют в поле.

10. Полученную невязку f_h распределяют с обратным знаком пропорционально длинам секций хода, т.е. вычисляют в графе 11 поправки v_i по формуле

 

(9)

 

где [L] – длина хода, км;

L_i – длина секции, км.

(Поправки вычисляют в мм, следовательно f_h берут в мм.)

11. Контроль вычисления поправок проверяют по формуле

 

(10)

 

12. Уравненные превышения вычисляют в графе 12

 

(11)

 

13. Уравненные отметки находят в графе 13 по формуле

 

(12)

 

Если уравнивание выполнено верно, то

 

(13)

 

14. Веса уравненных отметок промежуточных реперов определяют по формуле

 

(14)

 

где – длина всего хода, км;

– длина хода от начальной марки до репера с номером i, км;

– длина хода от репера i до конечной марки с номером, км.

15. Среднюю квадратическую ошибку уравненных отметок вычисляют по формуле

 

(15)

 

16. Ошибки самих ошибок находят по формуле

 

(16)

 

17. Из всех M_{H i} выбирают самую большую

 

max M_{H i} = M_{H слаб},

 

где M_{H слаб} – ошибка в слабом месте (примерно в середине хода).

Должно выполняться условие

 

M_{H слаб} £ D_пред,

 

где D_пред – предельная СКО положения точки по высоте в середине хода после уравнивания.

 

D_пред = М,

 

где М – СКО положения по высоте конечной точки хода до уравнивания.

 

 

где L, км – [L] – длина хода.

Если max M_{H i} £ то уравненные отметки соответствуют по точности III классу.

 

Всего подготовлено 10 вариантов каждого задания; по одному варианту на студента. Номер варианта N определяется единицами e индивидуального шифра студента. Например: шифр 99124, e=4, номер варианта N=4; шифр 00100, e=0, номер варианта N=10.

 

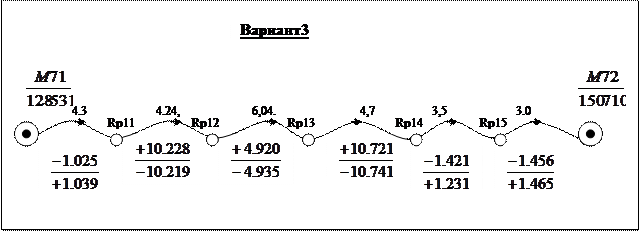
Варианты к контрольной работе №3

		Вариант 1
	Rp10