Примеры решений Методические указания
и варианты заданий для выполнения контрольной работы №1
по дисциплине «Линейная алгебра и математический анализ» для студентов заочной формы обучения направления 080100 (нормативный и сокращенный срок обучения)
Ростов-на-Дону
Задание 1. Решить систему линейных алгебраических уравнений методом Гаусса: Решение: Выпишем расширенную матрицу системы в виде таблицы. Будем обозначать строки матрицы C1,C2,C3 соответственно. Прямым ходом называется преобразование расширенной матрицы, целью которого является получение нулей под главной диагональю. Для этого используются линейные преобразования: сложение или вычитание строк с умножением на необходимые коэффициенты.
С2-2С1; С3-3С1;
С2:(-1); С3:(-1);
С3-2С2;
С3:4;
Далее можно преобразовывать систему таким же способом, как только что было выполнено, только целью в этом случае является получение нулей над диагональными единицами. Это действие называется обратным ходом. С1-3С3; С2-2С3;
С1-2С2;
В этом виде системы
|
- разрешенные переменные, их еще называют базисными переменными, а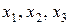 
совпадают со значениями свободных членов. В линейном программировании такое решение принято называть базисным решением. В данном примере базисное решение имеет вид: 
.
