Задание 2. Решить систему уравнений методом Крамера:
Решить систему уравнений методом Крамера:
Решение:
Тогда Вычисляя определители этих матриц, получаем Значения неизвестных вычисляются по формулам Крамера:
Решить систему уравнений с помощью обратной матрицы:
Решение:
Вычислим определитель матрицы Значит, обратная матрица существует. Вычислим алгебраические дополнения элементов матрицы:
Тогда решение системы получается умножением обратной матрицы на столбец свободных членов
Задание 3. Выяснить, является ли данная система векторов линейно зависимой или линейно независимой:
Решение: Система векторов линейно независима, если линейная комбинация этих векторов обращается в ноль только в том случае, когда все коэффициенты при данных векторах равны нулю, т.е. Проверим, являются ли вектора линейно зависимыми.
Преобразуем систему линейных уравнений методом Гаусса. Выпишем расширенную матрицу системы в виде таблицы (столбец свободных членов системы состоит только из нулей и не изменяется в процессе преобразований, поэтому его можно не записывать).
Значит,
Задание 4. Вычислить предел
Задание 5. Вычислить предел
Задание 6. Найти производную функции
Решение:
Задание 7. Найти производную функции, заданной неявно. Решение:
Задание 8. Пользуясь правилом Лопиталя найти предел Решение:
Задание 9. Составить уравнение касательной и нормали к графику функции Решение: Уравнение касательной имеет вид:
Уравнение нормали имеет вид:
Задание 10. Найти интервалы монотонности и экстремумы функции Решение:
Функция убывает при Точка Точка
Задание 11. Задана функция спроса Решение: Если
Из уравнения функции спроса найдем значение
Тогда
Задание 12. Найти частные производные Решение:
Задание 13. Дана функция Решение:
Литература
|


 ,
, 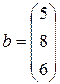 .
. ,
,  ,
,  .
. ,
,  ,
,  ,
, 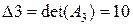 .
. ,
,  ,
,  .
.
 ,
, 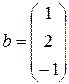 .
. , разлагая по первой строке:
, разлагая по первой строке: 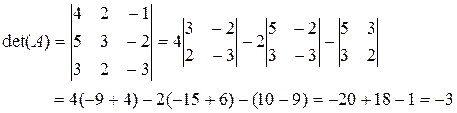
 ,
, ,
, ,
, ,
, ,
, ,
,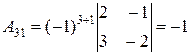 ,
,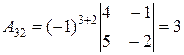 ,
,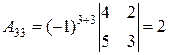 .
.

 .
.




 . Следовательно, система векторов линейно независима.
. Следовательно, система векторов линейно независима.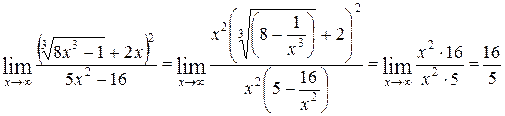







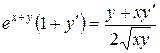
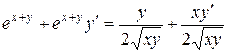



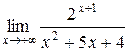


 в точке
в точке  :
: 
 ;
; ;
; 
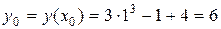




 ;
;

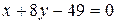
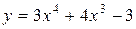

 - стационарные точки
- стационарные точки
 , возрастает при
, возрастает при  .
. не является точкой экстремума, т.к. производная не меняет знак при переходе через эту точку.
не является точкой экстремума, т.к. производная не меняет знак при переходе через эту точку. - точка минимума.
- точка минимума. - минимум функции.
- минимум функции. . Найти эластичность
. Найти эластичность  при заданных значениях цены или количества товара.
при заданных значениях цены или количества товара.  ,
, 


 при
при  ;
; ;
; .
.






 , точка
, точка  и вектор
и вектор  . Найти
. Найти  в точке
в точке  и производную в точке
и производную в точке 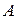 по направлению вектора
по направлению вектора 









