Теоретическое введение. Парная регрессия – уравнение связи двух переменных y и x: , где y – зависимая переменная (результативный признак); x – независимая
Парная регрессия – уравнение связи двух переменных y и x: Различают линейные и нелинейные регрессии. Линейная регрессия: y = a + bx + e. Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам. Регрессии, нелинейные по объясняющим переменным: · полиномы разных степеней y = a + b1x + b2x2 + b3x3 + e; · равносторонняя гипербола Регрессии, нелинейные по оцениваемым параметрам: · степенная · показательная · экспоненциальная Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессии, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака y от теоретических
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно a и b:
Можно воспользоваться готовыми формулами, которые вытекают из этой системы:
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции
и индекс корреляции
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а так же средняя ошибка аппроксимации. Средняя ошибка аппроксимации – среднее отклонение расчётных значений от фактических:
Доступный предел значений Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака y характеризует коэффициент (индекс) детерминации R2:
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
|

 , где y – зависимая переменная (результативный признак); x – независимая, объясняющая переменная (признак-фактор).
, где y – зависимая переменная (результативный признак); x – независимая, объясняющая переменная (признак-фактор). .
. ;
; ;
; .
. минимальна, т.е.
минимальна, т.е. .
.
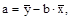
 .
. для линейной регрессии
для линейной регрессии  :
:
 – для нелинейной регрессии
– для нелинейной регрессии  :
: .
. .
. - не более 8-10%.
- не более 8-10%. .
.


