РАСЧЕТНАЯ ЧАСТЬ КОНТРОЛЬНОЙ РАБОТЫ
Задача 1. Моделирование времени выполнения заказа
клиента методом Монте-Карло.
Выполнение заказа включает три операции: 1 – приём и обработка заказа; 2 – документирование и отгрузка товара; 3 – доставка. Время выполнения каждой операции ti случайно и определено соответствующим законом распределения f(ti). Общее время, затрачиваемое на выполнение заказа, также случайно и определяется в виде суммы:
t0 = t1 + t2+ t3.
Необходимо смоделировать последовательность из 10 случайных значений t0, используя данные из табл.1.1–1.4 и формулы генераторов случайных чисел для разных законов распределения. Параметры законов распределения следует вычислить по формулам табл.1.1 через среднее и среднее квадратическое значения распределения после выбора исходных данных по последней цифре шифра зачётной книжки из табл.1.2. Исходные последовательности псевдослучайных чисел для генерации ti выбираются из табл.1.3 по двум последним цифрам шифра зачётной книжки следующим образом. Первое случайное число определяется на пересечении строки и столбца. Последующие числа выбираются построчно справа от первого. Для каждого шага вычислений необходимо выбрать новое случайное число. Например, для шифра 91 следует из табл.1.3 выбрать последовательность: 0.28, 0.207, 0.518, 0.286, 0.451, 0.263 и т.д. А для шифра 21 – 0.803, 0.442, 0.903, 0.792, 0.415 и т.д. Аналогично выбираются последовательности нормально распределённых чисел из табл.1.4.
Таблица 1.1
Законы распределения
| Наименование (обозначение)
| Плотность распределения
| Параметры
| | Нормальный (Н)
| 
|  , , 
| | Логарифмически нормальный (Л)
| 
| 
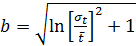 
| | Экспоненциальный (Э)
| 
| 
| | Равновероятный (Р)
| 
| 

|  – среднее значение; – среднее значение;  – среднее квадратическое отклонение – среднее квадратическое отклонение
| Таблица 1.2
Выбор данных для моделирования по последней цифре шифра
| Послед. цифра шифра
| Параметры распределения времени выполнения операций
| | t1, ч
| t2, ч
| t3, ч
| 
| 
| закон
| 
| 
| закон
| 
| 
| закон
| |
| 0.6
| 0.1
| Н
| 1.0
| 1.0
| Э
| 2.0
| 0.5
| Н
| |
| 1.1
| 1.1
| Э
| 1.8
| 0.3
| Н
| 2.5
| 1.1
| Л
| |
| 1.2
| 0.7
| Л
| 2.1
| 0.4
| Р
| 5.0
| 1.1
| Р
| |
| 1.4
| 0.3
| Р
| 2.9
| 1.3
| Л
| 4.0
| 4.0
| Э
| |
| 1.3
| 0.3
| Н
| 3.0
| 0.6
| Р
| 3.5
| 0.7
| Н
| |
| 1.5
| 1.5
| Э
| 2.5
| 0.6
| Р
| 3.0
| 1.3
| Л
| |
| 0.8
| 0.5
| Л
| 2.0
| 2.0
| Э
| 2.8
| 0.5
| Н
| |
| 0.9
| 0.9
| Э
| 1.5
| 0.3
| Н
| 4.8
| 4.8
| Э
| |
| 1.0
| 0.2
| Р
| 1.8
| 0.8
| Л
| 4.2
| 0.9
| Р
| |
| 0.7
| 0.2
| Н
| 1.9
| 0.4
| Р
| 3.3
| 3.3
| Э
| Таблица 1.3
Случайные равномерно распределённые в интервале [0,1] числа ξ
| Предпоследняяцифра
| Последняяцифра шифра
| |
|
|
|
|
|
|
|
|
|
| |
| 0,518
| 0,286
| 0,451
| 0,263
| 0,253
| 0,937
| 0,469
| 0,412
| 0,494
| 0,599
| |
| 0,834
| 0,157
| 0,333
| 0,160
| 0,334
| 0,924
| 0,487
| 0,675
| 0,174
| 0,972
| |
| 0,564
| 0,646
| 0,687
| 0,030
| 0,973
| 0,779
| 0,168
| 0,022
| 0,803
| 0,442
| |
| 0,903
| 0,792
| 0,415
| 0,995
| 0,663
| 0,218
| 0,538
| 0,499
| 0,995
| 0,862
| |
| 0,865
| 0,793
| 0,498
| 0,131
| 0,145
| 0,042
| 0,547
| 0,091
| 0,956
| 0,013
| |
| 0,704
| 0,181
| 0,127
| 0,517
| 0,605
| 0,079
| 0,183
| 0,456
| 0,861
| 0,042
| |
| 0,483
| 0,428
| 0,955
| 0,824
| 0,071
| 0,904
| 0,736
| 0,632
| 0,889
| 0,292
| |
| 0,109
| 0,979
| 0,457
| 0,762
| 0,893
| 0,180
| 0,112
| 0,347
| 0,596
| 0,859
| |
| 0,025
| 0,641
| 0,235
| 0,057
| 0,248
| 0,921
| 0,398
| 0,023
| 0,905
| 0,947
| |
| 0,815
| 0,563
| 0,369
| 0,446
| 0,319
| 0,791
| 0,508
| 0,055
| 0,280
| 0,207
|
Таблица 1.4
Нормально распределённые случайные числа η
| Предпоследняя цифра
| Последняя цифра шифра
| |
|
|
|
|
|
|
|
|
|
| |
| 0,428
| 0,916
| 0,892
| -1,700
| -0,031
| -0,624
| -0,704
| -0,392
| -1,613
| -0,723
| |
| -1,185
| -1,190
| -1,449
| 1,908
| 0,630
| -0,754
| 1,724
| 0,268
| -0,148
| -1,905
| |
| -0,275
| -0,409
| -0,160
| -2,485
| -1,741
| -1,377
| 0,273
| 1,661
| 0,242
| -1,370
| |
| 0,294
| 1,469
| -0,221
| 0,843
| 1,281
| -0,629
| -0,047
| -2,395
| 0,211
| -0,190
| |
| -0,003
| -1,481
| -0,474
| -0,902
| 0,628
| -1,575
| -0,803
| 0,477
| 0,125
| 1,310
| |
| 0,300
| -0,302
| 0,064
| 1,101
| -0,568
| -0,370
| -2,769
| -0,732
| 0,035
| -0,298
| |
| -1,013
| -0,219
| -0,371
| -0,108
| -1,330
| 1,253
| -1,400
| -1,772
| 0,194
| -0,120
| |
| 0,687
| -0,212
| -0,425
| 1,244
| 1,497
| -1,340
| 0,837
| -0,696
| -0,284
| -0,110
| |
| -1,121
| 0,251
| -2,742
| -1,394
| -0,742
| -0,752
| -0,375
| -0,473
| 1,051
| -1,073
| |
| 0,164
| 0,021
| 0,316
| -1,227
| 0,186
| 0,439
| -0,329
| 1,012
| 0,151
| -0,014
| Задача 2. АВС – анализ прибыльности товаров.
Заданы объёмы продаж товаров по номенклатуре. Необходимо проанализировать и классифицировать товары с делением на три группы (группы А-В-С), используя в качестве критерия объем продаж. Группы АВС определяются аналитически и графически в виде диаграммы Парето. Исходные данные выбираются из табл. 2.1 по шифру зачётной книжки.
Таблица 2.1
Исходные данные для выбора варианта выборки к задаче 2
| Товар
| Последняя цифра номера зачётной книжки
| |
|
|
|
|
|
|
|
|
|
| | Т1
|
|
|
|
|
|
|
|
|
|
| | Т2
|
|
|
|
|
|
|
|
|
|
| | Т3
|
|
|
|
|
|
|
|
|
|
| | Т4
|
|
|
| 152.5
|
|
|
|
|
| 147.5
| | Т5
|
| 70.5
|
|
| 72.5
| 69.5
|
| 71.5
| 68.5
| 72.5
| | Т6
|
|
| 79.5
| 80.5
|
| 81.5
|
| 82.5
| 81.8
| 79.3
| | Т7
|
|
| 39.5
| 39.7
| 40.3
| 40.5
|
|
| 41.2
| 41.5
| | Т8
|
|
|
|
| 109.5
| 108.5
|
| 110.5
| 111.5
| 107.5
| | Т9
|
| 120.5
|
|
| 122.5
|
| 119.5
|
| 118.5
| 121.5
| | Т10
|
|
|
| 227.5
|
| 229.5
| 230.5
|
| 229.7
| 228.5
| | Т11
|
| 48.6
|
| 49.5
| 49.8
| 50.4
|
| 51.3
| 51.6
|
| | Т12
|
| 57.8
|
| 58.4
|
| 59.5
| 60.4
|
| 61.6
|
| | Т13
|
|
| 89.5
| 90.4
| 90.7
|
| 91.5
| 91.8
|
| 92.6
| | Т14
|
|
| 110.4
| 110.9
|
| 111.5
| 109.5
|
| 108.6
| 112.4
| | Т15
|
| 118.6
|
| 119.4
| 120.5
| 120.8
|
| 121.5
|
| 122.4
| | Т16
|
|
| 138.5
|
| 139.5
| 140.5
|
| 141.4
| 141.8
|
| | Т17
|
|
| 159.5
| 159.8
| 160.4
|
| 161.4
| 161.8
|
| 162.3
| | Т18
|
|
| 253.5
|
|
| 250.5
| 249.5
|
| 248.5
|
| | Т19
|
| 270.5
|
| 271.3
| 269.5
| 271.8
|
| 272.4
| 272.9
| 273.1
| | Т20
|
|
| 303.5
| 303.3
|
| 302.5
|
| 305.5
| 302.7
| 301.6
| | Т21
|
|
| 310.5
| 309.7
| 309.2
|
| 308.7
| 308.2
|
| 307.5
| | Т22
|
|
| 278.6
|
| 279.5
| 280.5
|
| 281.5
|
| 282.5
| | Т23
|
|
| 209.3
| 209.6
| 210.3
| 210.9
| 211.2
| 211.7
|
| 212.5
| | Т24
|
|
| 192.5
|
| 191.5
| 190.5
| 189.5
|
| 188.6
| 187.8
| | Т25
|
| 139.5
| 137.5
|
| 138.5
|
| 140.5
|
| 141.5
|
| | Т26
|
|
| 129.5
| 130.5
| 130.8
| 131.5
| 131.3
|
| 132.4
| 132.7
| | Т27
|
|
| 94.5
| 95.3
| 95.7
|
| 96.4
| 96.8
|
| 97.4
| | Т28
|
| 79.7
| 79.5
| 80.3
| 80.6
| 80.9
|
| 81.3
| 81.6
|
| Задача 3. Определение вероятности отказа в поставке товара
клиенту методами схемной надёжности.
Необходимо определить вероятность нарушения контрактных условий доставки товара в цепи поставки, состоящей из 5 элементов (посредников) с резервированием. Характеристики надёжности (безотказность) основных и резервных элементов и структура цепи выбираются из табл.3.1 – 3.2. Элементы с резервированием выделены затенением (два значения в ячейке таблицы – в числителе основной элемент, а в знаменателе параллельно включённый резервный).
Таблица 3.1
Структура цепи поставок из 5 элементов
| Последняяцифра шифра
| Элементы цепи поставок
| | первый
| второй
| третий
| четвёртый
| пятый
| |
|
|
|
|
|
| |
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
| |
|
|
|
|
|
| |
| |
|
|
|
|
|
| |
|
| |
|
|
|
|
|
| |
|
| |
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|
| |
| |
|
|
|
|
|
| |
|
| |
|
|
|
|
|
| |
|
Таблица 3.2
Характеристики надёжности элементов цепи поставок к задаче 3
| Предпоследняя цифра шифра
| Вероятность безотказной работы элементов цепи, pj
| | 1-й
| 2-й
| 3-й
| 4-й
| 5-й
| |
| 0.80
| 0.90
| 0.95
| 0.85
| 0.92
| |
| 0.78
| 0.92
| 0.97
| 0.89
| 0.90
| |
| 0.87
| 0.93
| 0.98
| 0.88
| 0.91
| |
| 0.83
| 0.94
| 0.85
| 0.81
| 0.93
| |
| 0.88
| 0.96
| 0.75
| 0.82
| 0.94
| |
| 0.90
| 0.89
| 0.88
| 0.95
| 0.95
| |
| 0.90
| 0.88
| 0.93
| 0.93
| 0.96
| |
| 0.93
| 0.79
| 0.91
| 0.94
| 0.88
| |
| 0.78
| 0.91
| 0.93
| 0.77
| 0.79
| |
| 0.94
| 0.93
| 0.89
| 0.79
| 0.86
|
Задача 4. Прогнозирование спроса на товары методом
наименьших квадратов (МНК) с учётом сезонности.
По данным, представленным в виде динамического ряда поквартальных продаж (табл.4.1 – 4.2), необходимо построить траекторию тренда и сделать прогноз на два квартала вперёд. Особенностью динамического ряда является явно выраженная сезонность, которая учитывается с помощью тригонометрической функции. Модель тренда имеет вид
 , j =1,2,…,8, , j =1,2,…,8,
где: Zj – объем продаж; h – частота колебаний; tj – текущее время (квартал); a, b – искомые коэффициенты модели.
Пояснения к задаче:
1. Текущее время tj определяется следующим образом
t1 = k, t2 = t1 +1, t3 = t2 +1, t4 = t3 +1 и т. д.,
где k – номер квартала, с которого начинаются наблюдения (табл.4.1). Например, для шифра 21 t1 =2, t2 =3, t3 =4 и.т.д. Ряд продаж для данного шифра 201, 260, 190, 122, 210, 265, 209, 120.
2. Частота сезонных колебаний определяется из соотношений
1= Cos(2π) = Cos(hr), откуда h = 2π/r,
где r – количество кварталов между двумя соседними пиками продаж (период). Например, если первый пик приходится на t3, а второй на t7, то r =4 и, следовательно, имеем h = π/2. Для определения r следует построить график эмпирических значений продаж (табл.4.2).
3. После вычисления частоты необходимо выполнить замену переменной Yj=Cos(htj). Получим новую модель Zj=a+bYj, коэффициенты которой a и b необходимо найти, используя метод наименьших квадратов.
Результаты расчётов представить в виде графика Z(t), включая прогнозные значения для t9 и t10.
Таблица 4.1
Номер квартала, с которого начинаются наблюдения k
| Номер
| Предпоследняя цифра шифра зачётной книжки
| |
|
|
|
|
|
|
|
|
|
| | k =
|
|
|
|
|
|
|
|
|
|
| Таблица 4.2
Динамический ряд продаж, начиная с k -го квартала
| Последняяцифра шифра
| Объем продаж/квартал
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|
МЕТОДИКА ИЗУЧЕНИЯ МОРФЕМНОГО СОСТАВА СЛОВА В НАЧАЛЬНЫХ КЛАССАХ В практике речевого общения широко известен следующий факт: как взрослые...
СИНТАКСИЧЕСКАЯ РАБОТА В СИСТЕМЕ РАЗВИТИЯ РЕЧИ УЧАЩИХСЯ В языке различаются уровни — уровень слова (лексический), уровень словосочетания и предложения (синтаксический) и уровень
Словосочетание в этом смысле может рассматриваться как переходное звено от лексического уровня к синтаксическому...
Плейотропное действие генов. Примеры. Плейотропное действие генов - это зависимость нескольких признаков от одного гена, то есть множественное действие одного гена...
|
Сосудистый шов (ручной Карреля, механический шов). Операции при ранениях крупных сосудов 1912 г., Каррель – впервые предложил методику сосудистого шва.
Сосудистый шов применяется для восстановления магистрального кровотока при лечении...
Трамадол (Маброн, Плазадол, Трамал, Трамалин) Групповая принадлежность
· Наркотический анальгетик со смешанным механизмом действия, агонист опиоидных рецепторов...
Мелоксикам (Мовалис) Групповая принадлежность
· Нестероидное противовоспалительное средство, преимущественно селективный обратимый ингибитор циклооксигеназы (ЦОГ-2)...
|
|


 ,
, 


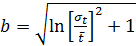






 – среднее значение;
– среднее значение;  – среднее квадратическое отклонение
– среднее квадратическое отклонение
 , j =1,2,…,8,
, j =1,2,…,8,


