РЕШЕНИЯ 3 страница
путевка в Фингалию
3) Информация о двух возможных вариантах приобретаемого количества путевок позволяет составить систему из двух уравнений с двумя неизвестными:
где К и Ф – количество путевок в Каркодайл и Фингалию соответственно. Решение этой системы уравнений позволяет найти К = 7 и Ф = 9. 4) Подставляя эти цифры в уравнение, соответствующее второму варианту сделки, можно получить искомое количество банок икры, выделенных для этой сделки:
51. 1) В исходном положении сосуд № 1 содержит 1,1л тоника, а сосуд № 2 – 0,5 л джина. 2) Из сосуда № 1 в сосуд № 2 переливается 0,5 л тоника (чтобы удвоить там количество жидкости). Теперь в сосуде № 1 осталось 0,6 л тоника, а в сосуде № 2 оказался 1 л смеси, состоящей поровну из джина и тоника. 3) Из сосуда № 2 в сосуд № 1 переливается 0,6 л (столько, сколько оставалось в сосуде № 1) смеси, состоящей из 0,3 л джина и 0,3 л тоника. Теперь в сосуде № 1 0,3 л джина и 0,9 л тоника, а в сосуде № 2 осталось 0,2 л джина и 0,2 л тоника. 4) Из сосуда № 1 в сосуд № 2 переливается 0,4 л (чтобы удвоить там количество) смеси, содержащей 0,1 л джина и 0,3 л тоника (смесь в сосуде № 1 имеет соотношение джина и тоника 1: 3). После всего этого количество жидкости в сосудах становится по 0,8 л. В сосуде № 1 образовалась смесь из 0,6 л джина и 0,2 л тоника (3: 1 – крепкий коктейль). В сосуде № 2 – смесь из 0,3 л джина и 0,5 л тоника (3: 5 – слабый коктейль). 52. Используя формулу сложных процентов для приведения взносов к моменту покупки (см. задачу 150), получим:
41,7 тыс. у. д. ед. – это и есть действительная стоимость дома на момент покупки. Следовательно, покупатель, назвав сумму 40 тыс. у. д. ед., предложил весьма выгодную для себя сделку. 53. Обозначив количество голосов, поданных за различные виды пасты, их начальными буквами, можно представить результаты маркетингового исследования в таком виде:
Суммируя первые три выражения, получим:
Складывая (*) и (**), получим:
4А = 4500, откуда А = 1125 голосов.
Соответственно:
54. 1) Общая прибыль от операции купли-продажи квартир составляет 14% - 11 % = 3 %. Следовательно, цена покупки обеих квартир равна 500 тыс. у. д. ед. (3 % от 500 = 15, т. е. 515-500). 2) Обозначая цену покупки 1-й квартиры через х, а 2-й квартиры через у, можно записать условие задачи следующим образом:
Решим систему из двух уравнений с двумя неизвестными.
откуда
Цена продажи 1-й квартиры 280 х (1+0,14) = 280 х 1,14 = 319,2 тыс. у. д. ед. Цена продажи 2-й квартиры 220 х (1-0,11) = 220 х 0,89 = 195,8 тыс. у. д. ед.
55. Обозначив через х количество оплаченных компьютеров (без премии), через у – стоимость каждого оплаченного компьютера, а через у – количество премиальных компьютеров, можно представить условие задачи следующим образом:
Решим полученную систему из трех уравнений с тремя неизвестными:
Подставляя значение у в (2), получим:
Подставляя значение х в (3), получим:
Итак, 1) без учета премии было приобретено 16 компьютеров по цене 750 у. д. ед.; 2) в виде премии было получено 2 компьютера.
56. Обозначив через х количество первоначально оплаченных дубленок, а через у – цену дубленки без учета стимулирования, можно записать условие задачи следующим образом:
Решая систему из двух уравнений с двумя неизвестными и подставляя значение у из (1) в (2), получим:
Решая квадратное уравнение (*) по стандартной формуле, получим:
х1 = 24 (х2 не подходит, так как отрицательно). 57. Обозначая месячный спрос и цену до ее снижения через х и у соответственно, записываем условие задачи так:
Решая систему из двух уравнений с двумя неизвестными, приходим к следующему квадратному уравнению с одним неизвестным:
х2 + 400 х - 960 000 = 0.
Применяя стандартную формулу для решения квадратных уравнений, получим:
х1 = 800 единиц; (х2 не подходит, так как отрицательно),
После сезонного снижения цены до 30 - 10 = 20 у. д. ед. месячный спрос повышается до 800 + 400 = 1200 единиц. 58. Обозначим через х первоначальное количество копеек. Тогда в конце игры будет соответственно И условие задачи можно записать так:
100х + у = 2.
Откуда следует:
98х – 99у = 0, (*) х и у должны быть обязательно целыми числами (это рубли и копейки). Анализируя условие (*), можно сообразить, что эта целочисленность будет иметь место, лишь если у = 98.
59. Когда менеджер начал обход, у него оставалась половина рабочего времени. Эта половина состоит из трех частей: две – на обход и одна в кабинете. Следовательно, на обход менеджер затратил 60. Обозначим участников переговоров А, Б и В. Представим ход рассуждений участника А: «Участник Б думает, что его лысина прикрыта, и смеется над В. Но если бы он видел, что у меня прическа в порядке, то был бы удивлен смеху В, так как в этом случае у В не было бы повода улыбаться. Однако Б не удивлен, значит, он думает, что В смеется надо мной. Следовательно, моя лысина не прикрыта». 61. Из слов хозяина черной шевелюры следует, что у Белова волосы могли быть только черными или рыжими, у Чернова – белыми или рыжими, у Рыжова – черными или белыми. Это означает, что тронуть рукой свою черную шевелюру мог только банкир Белов или юрист Рыжов. Поскольку на слова черноволосого среагировал банкир, то он не может быть тем, кто говорил. Следовательно, черноволосый – юрист Рыжов. Значит, банкир Белов не черноволосый. Не может быть он и блондином. Следовательно, Белов – рыжий. Белые волосы остаются для предпринимателя Чернова. 62. Бизнесмен Жук солгал. Дело в том, что утверждение «неверно, что все бизнесмены лгуны» равносильно тому, что «не все бизнесмены лгут». А раз так, то Жук мог и солгать. 63. Принимая общее количество учеников Пифагора за х, можно записать условие задачи так:
откуда х =28. 64. Принимая долю мужчин за х, можно записать:
65. Принимая число присутствующих на собрании за х, можно записать:
Откуда х = 130 человек. Всего в коллективе 130 + 0,2 х 130 = 156 человек.
66. Во-первых, для того чтобы не пропустить момент, когда собеседник начнет поглядывать на свои часы, – это первый сигнал к тому, что пора закругляться. А во-вторых, для того чтобы правильно отреагировать, когда партнер по переговорам снимет часы и станет трясти ими у себя над ухом, проверяя, не остановились ли они. 67. Обозначим количество участников деловой встречи через х. Тогда количество договоров, заключенных каждым из участников, равно х - 1 (исключается договор с самим собой). А всего на встрече будет заключено х(х - 1) договоров. Но эти договоры должны быть парными (на двух участников – один договор). Поэтому фактически договоров будет в два раза меньше:
Следовательно
откуда х = 15.
68. При гиперинфляции найденный кошелек кладут в карман, а деньги из него выбрасывают.
69. Необходимо заполнить доверху 9-литровое ведро и дважды с помощью 4-литрового ведра отлить из него ровно 8 литров воды. Оставшийся 1 литр воды вылить в пустое 4-литровое ведро. Снова наполнить 9-литровое ведро и отлить из него 3 литра воды в 4-литровое (там уже есть 1 литр), заполнив его доверху. В 9-литровом ведре при этом останется ровно 6 литров воды.
70. Необходимо вначале отловить 100 карпов, пометить их и выпустить обратно. Через некоторое время, когда рыбы успокоятся, снова отловить 100 карпов и сосчитать, сколько среди них меченых. К примеру, меченых рыб оказалось 4. Это означает, что в водоеме 4 % меченых рыб. Но, с другой стороны, мы знаем, что меченых рыб 100. Следовательно, 100 рыб составляют 4 % от общего количества их в пруду. Значит, 100 % - это
71. 1) Вероятность того, что первый попавшийся вам по приезде в Москву человек – ваш единственный знакомый в этом городе, равна:
2) Вероятность отгадать в лотерее 6 номеров из 49 по формулам теории вероятностей равна:
где С649 – сочетание из 49 элементов по 6. Следовательно, вероятность отгадки равна
т. е. примерно в полтора раза меньше.
72. Возможно. На этот счет существует специальная теорема. Практическое решение данной задачи требует, однако, сложных расчетов. 73. Водителям поменяться машинами. 74. В момент выхода железнодорожного состава из Москвы в пути находится 8 встречных составов, в том числе один, входящий в это время в Москву, и один, выходящий из Владивостока. Все 8 составов будут встречными. Но этого мало. За те 7 дней, что москвичи будут в пути, из Владивостока успеет выйти еще 7 составов (в том числе один – в момент прихода московского поезда во Владивосток). Итого 8 + 7 = 15 составов, т. е. письма могут быть получены 15 раз. 75. До третьего этажа 2 пролета лестниц, до шестого – 5. Следовательно, т. е. в два с половиной раза.
76. Вероятность выигрыша рассчитывается по формулам теории вероятностей:
Необходимые формулы можно найти в любом математическом справочнике.
п – общее количество билетов, k – количество билетов, содержащих выигрыш, т – количество купленных билетов, Clk – количество билетов, выигрыш по которым нас интересует.
Подставляя соответствующие значения, получим:
77. 0,80 х 0,80 х 0,60 - 0,38, т. е. 38 %.
78. Отгадывание 6 цифр из 49 допускает только одно правильное решение – ни в одной из шести вычеркнутых цифр нельзя ошибиться. При отгадывании пяти номеров разрешается допустить ошибку в одном (любом) из шести «правильных» номеров. При этом «правильный» номер заменяется одним из «неправильных», которых насчитывается 49 - 6 = 43. Число таких замен равно количеству пар чисел в диапазоне от 1 до 49. Так, цифра 1 может быть заменена на 7, 8, 9 и т. д., вплоть до 49. То же самое с цифрой 2 и т. д. до 6. Вот как это выглядит:
Число таких пар замен равно 6 х 43 = 258. Следовательно, вероятность отгадать 5 цифр равна:
1) Аналогичным путем рассчитывается вероятность отгадать 4 цифры:
больше, чем 5 номеров.
2) 3 цифры: чем 5 номеров.
79. В соответствии с правилами теории статистических решений необходимо свести условие задачи в следующую таблицу:
Наилучшим решением признается такое, при котором сумма произведений (время на число голосов) будет минимальной. В данном случае это решение «прямо».
80. В соответствии с теорией статистических решений общий результат Энди равен 0,5 х 50 + 0,5 х (-10) = 20 долларам. Поскольку этот результат положителен, решение Энди должно быть: «Вперед, за должником».
81. Задача решается методами теории игр с использованием принципа «рассчитывай на худшее». Условие задачи сводится в следующую таблицу:
Вначале для каждого из решений находится худший результат, который записывается справа от таблицы. Затем из худших результатов выбирается лучший. В данном случае это 1000 у. д. ед. Решение, соответствующее этому результату, – «вернуться домой» является наилучшим.
82. Задача решается методами теории игр с использованием принципа «рассчитывай на худшее». Условие задачи сводится в следующую таблицу:
При составлении таблицы мы рассуждали так. Если день рождения у Марины не сегодня и вы не принесете подарка, то положение будет нейтральным. Если у нее не день рождения и вы примчитесь с букетом, то максимум, чем вы рискуете, это подвергнуться проверке на трезвость. Если у нее действительно день рождения и вы вовремя вспомнили об этом, то заслужите искреннюю благодарность. Если же в этом случае вы не принесете ничего – вы человек пропащий. Выражая результаты в очках, вы вынуждены пользоваться произвольными числами. Это, однако, не должно вас смущать: важно, чтобы они не противоречили жизненному опыту. Так, отсутствие подарка в день рождения не менее чем в 10 раз хуже противоположной ситуации (в этом нетрудно убедиться экспериментально). Из таблицы по правилам, приведенным в решении задачи 81, находится лучший из худших результатов и соответствующее ему решение – «с цветами».
83. Обозначая среднюю скорость автомобиля через х, а расстояние между городами – l, можем записать, чему будет равно время, затраченное на поездку туда и обратно:
откуда х = 48 км/ч.
84. Задача решается методами теории статистических решений. Условие задачи сводится в следующую таблицу:
Цифры, оценивающие ожидаемый результат, получены из следующих соображений: – при полете самолетом в случае тумана агент не потеряет день работы, который принесет 1500 у. д. ед., и получит у иногороднего клиента заказ по телефону, что даст еще 500 у. д. ед., итого 2000 у. д. ед.; – если при полете самолетом будет ясная погода, агент успеет получить 1500 у. д. ед. дома и 3000 – от иногороднего клиента, итого 4500 у. д. ед.; – в случае поездки поездом независимо от погоды агент получит у иногороднего клиента заказ на 3000 у. д. ед. Расчеты, приведенные справа от таблицы, показывают, что наибольший среднеожидаемый результат соответствует решению «лететь самолетом».
85. Обозначим годовой доход Д, годовой страховой взнос Вс. Тогда по условию задачи можно написать:
Откуда
86. Обозначая прибыль ПР, выплаты страховых премий в год Всп, а затраты на организацию страховой деятельности Зсд, по условию задачи можно написать:
87. Обозначая искомое дневное задание через х и применяя формулу суммы членов арифметической прогрессии, можно записать условие задачи следующим образом:
Отсюда следует, после преобразований, квадратное уравнение:
Отсюда
Поскольку дневное задание – количество деталей – должно быть целым числом, искомое решение х 1 = 13 деталей.
88. По формуле теории вероятностей
89. По формуле теории вероятностей число размещений с повторениями (букв) из п элементов
Отсюда
90. По формуле теории вероятностей решение равно числу перестановок, деленному на число размещений с повторениями перестановок из 4! элементов:
91. 1) Сокращение производительности труда в день при этом равно:
а в рабочую неделю 0,033 х 6 = 0,198. Следовательно, производительность труда должна вырасти на 19,8 %. 2) Сокращение производительности труда в день при этом равно:
а в рабочую неделю 0,013 х 6 = 0,078. Следовательно, производительность труда должна вырасти на 7,8 %. 3) Сокращение производительности труда в день при этом равно:
а в рабочую неделю 0,053 х 6 = 0,318.
Следовательно, производительность труда должна вырасти на 31,8 %. 92. План января был выполнен на 100 + 6 = 106%, план февраля - на 106 + (6 % от 106) = 106 + 6,36=112,36%, план марта – на 112,36 + (6 % от 112,36) = 112,36 + 6,74 = 119,1%. За все три месяца план был выполнен на 106 + 112,36 + 119,1 = 337,46 %, что соответствует среднемесячному 337,46:3 = 112,49 %. Следовательно, среднемесячный план был перевыполнен на 112,49 - 100 = 12,49 %. 93. Первая бригада отработала 5 х 10 = 50 человеко-дней, вторая бригада – 7 х 4 = 28, объединенная бригада – 12 х 5 = 60. Всего общая работа составила 50 + 28 + 60 = 138 человеко-дней. А заработок на одного рабочего той и другой бригады равен 1518: 138 = 11 уд. ед. в день. Следовательно, каждый рабочий в первой бригаде получил:
11 х (10 + 5) = 165 у. д. ед.,
а каждый рабочий во второй бригаде
11 х (4 + 5) = 99 у.д.ед. 94. Предприятие № 1 за месяц выполняет
заказа, предприятие
предприятие № 3 - 14 + 19 = 33 %. А все три предприятия за один месяц выполняют 14 + 19 + 33 = 66 % заказа. Следовательно, весь заказ (100%) все три предприятия выполнят за 95. Обозначая количество изделий, планируемых к выпуску за год, через х, можно записать условие задачи следующим образом:
Отсюда, после преобразований, х= 28 000 изделий.
96. Обозначая искомый срок одновременной работы всех цехов над заказом через х, можно представить условие задачи следующим образом:
Отсюда х = 12 дней. Итак, 1) выпуск цеха № 1 должен составлять 100 х 12 = 1200 единиц, выпуск цеха № 2 – 40 х 12 = 480, выпуск цеха № 3 - 50 х 12 = 600; 2) срок совместной работы над заказом должен быть равен 12 дням.
97. В I квартале выполнено 25 % Всего за год выполнено 119,17 % годового плана. 1) Перевыполнение плана составляет 119,17 – 100 = 19,17 %. 2) Это соответствует
98. Соотношение 3: 7: 15 означает, что линейных руководителей должно быть Отсюда количество принятых линейных руководителей равно 15, функциональных руководителей – 35 и мастеров – 45. 99. Обозначая через х плановое время выпуска 40 комбайнов, можно записать условие задачи следующим образом:
После преобразования получим х2 – х - 20 = 0. Решая квадратное уравнение по стандартной формуле, получим:
х1 = 5 дней (х2 не подходит, так как отрицательно). Следовательно, фактически 36 комбайнов были выпущены за 5 - 2 = 3 дня. При этом ежедневно выпускалось 100. Обозначив через х количество участков, нарезанных в первой части земли, можно записать условие задачи следующим образом:
После преобразований получим х2 + 25х - 150 = 0. Решая квадратное уравнение по стандартной формуле, получим:
х1 = 5 участков (х2 не подходит, так как отрицательно). Следовательно, 1) количество участков, нарезанных в первой части земли, равно 5, а во второй – 5 + 15 = 20; 2) площадь участка в первой части земли равна 2 га, а во второй – 1 га. 101. Обозначая первоначальное количество линий через х, можно представить условие задачи в следующем виде:
|






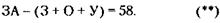

















 рубля и х копеек.
рубля и х копеек.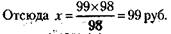
 от половины, т. е.
от половины, т. е.  рабочего времени.
рабочего времени.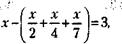

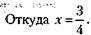

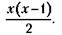




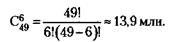








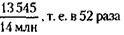


























 годового плана, во II квартале – 25 х 1,05 = 26,25 %, в III квартале - 26,25 х 1,15 = 30,19 %, в IV квартале - 30,19 х 1,25 = 37,73 %.
годового плана, во II квартале – 25 х 1,05 = 26,25 %, в III квартале - 26,25 х 1,15 = 30,19 %, в IV квартале - 30,19 х 1,25 = 37,73 %. единицам продукции.
единицам продукции. или 12%, функциональных руководителей –
или 12%, функциональных руководителей –  , или 28 %, и мастеров –
, или 28 %, и мастеров –  , или 60 %. Фактически же линейных руководителей оказалось 12 % + (25 % от 12 %) = 15 %, функциональных руководителей - 28 % + (25 % от 28 %) = 35 %, а мастеров - 60 % - (25 % от 60 %) = 45 %. Общий процент нанятого персонала составляет, таким образом, 15 + 35 + 45 = 95 %, что соответствует 95 принятым работникам.
, или 60 %. Фактически же линейных руководителей оказалось 12 % + (25 % от 12 %) = 15 %, функциональных руководителей - 28 % + (25 % от 28 %) = 35 %, а мастеров - 60 % - (25 % от 60 %) = 45 %. Общий процент нанятого персонала составляет, таким образом, 15 + 35 + 45 = 95 %, что соответствует 95 принятым работникам.







