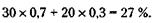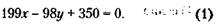РЕШЕНИЯ 5 страница
Итак, экспедитор покупает: 15 единиц радиоаппаратуры, 1 единицу одежды и 4 единицы бытовой техники.
129. Не только не переоценивает, но даже преуменьшает. Возьмем в руки самый подробный каталог товаров. Вряд ли он будет иметь более 1000 страниц. Откроем его посередине, на 500-й странице, и зададим 1-й вопрос: «Задуманный товар находится на этой странице или после нее?» Получив ответ, мы уменьшаем количество претендентов на задуманный товар ровно в 2 раза. Продолжая таким же образом «половинить» каталог, на 10-м вопросе мы дойдем до одной его страницы, на которой и будет искомый товар. Далее подобным же путем найдем один из двух столбцов, в которых располагаются товары (11-й вопрос). В столбце вряд ли будет более 10 товаров. Чтобы «споловинить» и их, потребуется еще максимум 4 вопроса. Итого 15 вопросов, и задача решена. 130. Действие чашечных весов основано на принципе рычага. Если правое плечо весов имеет длину П, левое – Л, и грузы, которые мы взвешиваем на правой и левой чашках, равны соответственно Рп и Рл, то должно действовать известное из физики равенство:
Поскольку весы неисправны, при первом взвешивании вес гири Г соответствует хкг товара, а при втором взвешивании – укг товара. Равновесие наступает при следующем равенстве: П х Г = Л х х – для первого взвешивания; Л х Г = П х х – для второго взвешивания. Из этих соотношений следует, что
При этом общий вес товара равен:
Из алгебры известно, что
(кроме случаев, когда
Значит, фактический вес товара больше, чем полученный в результате предложенного способа взвешивания.
131. После первой замены бензина на колонке оставалось 36 - 12 = 24 т высококачественного бензина. При этом в одном литре смеси высококачественный бензин составлял При второй замене в 9 т израсходованной смеси содержалось А в одном литре смеси – соответственно
После третьей замены в 8 т израсходованной смеси содержалось 14 т из 36 – это 39 % высококачественного бензина и 61 % (100 - 39) низкосортного. 132. 150 т. 133. Пожалуй, дешевле всего будет перенести увеличенное изображение небольшого часового циферблата на экран, помещенный на башне, с помощью оптического проектора. 134. Обозначая стоимость клипсов через Кл, броши – Бр, кольца – Кол и заколки – Зак, можно по условию задачи составить следующие два уравнения:
Совместное решение уравнений (1) и (2) даст искомый результат:
135. Предположим, вторая крестьянка имела в К раз больше яиц, чем первая. Так как они обе выручили одинаковые суммы, из сделанного предположения следует, что первая продавала яйца в К раз дороже, чем вторая. Если бы перед торговлей они поменялись яйцами, то у первой было бы в К раз больше яиц, чем у второй, и она продавала бы их в К раз дешевле. При этом она выручила бы денег в К х К = К2раз больше второй. Из этого следует отношение их выручек:
Деля 100 яиц в отношении 3: 2, получим, что у первой крестьянки было 60 яиц, а у второй - 40. 136. Норма прибыли (рентабельность) рассчитывается по формуле:
где НРПР – норма прибыли, ПР – прибыль, З – затраты.
137. Из формулы, приведенной в решении задачи 136, следует:
где В –выручка. Откуда
138. Норма накопления (НН) рассчитывается по формуле:
где Пнак – масса прибыли, направленная на накопление; Ппот – масса прибыли, направленная на потребление.
139. По формулам, приведенным в решении задач 136 и 137:
140. По формулам, приведенным в решении задачи 136, следует:
141. При горизонтальной организации каналов распределения товаров (см. рис.) каждый из производителей стремится направить свой товар по каналам, обеспечивающим наибольшую прибыль. При этом интересы производителей сталкиваются: один и тот же канал может оказаться привлекательным для обоих производителей, а пропускная способность каждого канала ограничена. В итоге стихийно складывается распределение, один из возможных вариантов которого показан на рисунке. При этом производитель товаров А получает прибыль, реальную сумме произведений единиц товара, направляемых каждому из потребителей, на соответствующие эффективности.
Прибыль производителя товара А = 10 х 16 + 30 x 10 + 20 x 8 = 620. Аналогично рассчитывается прибыль производителя товара Б: 40 х 12 + 0 х 18 + 0 х 6 = 480. Производитель товара А оказался в явном выигрыше. Казалось бы, что может быть для него лучше? Не будем, однако, торопиться с выводами. Рассмотрим вертикальную организацию каналов распределения товаров (см. рис.). В этом случае распределение товаров осуществляется в интересах не отдельного производителя товара, а системы в целом: принимается такое распределение, при котором суммарная прибыль обоих производителей будет максимальной. Для нахождения такого распределения (оно называется оптимальным) используются специальные методы. В простейших задачах данного типа решение может быть получено и глазомерно, путем подбора. На рисунке показано такое оптимальное распределение. Найдем величину суммарной прибыли обоих производителей товаров. Общая прибыль производителей товаров А и Б равна:
50 x 16 + 0 x 10 + 10 x 8 + 0 x 12 + 30 x 18 + 10 x 6 = 1480.
Это существенно (на 35 %) больше, чем суммарная прибыль при горизонтальном распределении (620 + 480 = 1100). Разделив соответствующую вертикальному распределению общую прибыль пополам (1480: 2), получим 740 единиц, что значительно больше, чем прибыль победителя при горизонтальном распределении товара (740 - 620 = 120). 142. Стоимость оптимальной партии товара (Попт) рассчитывается по формуле:
где Г – годовая стоимость заказа, Изг – стоимость издержек изготовления партии товара, Хр – стоимость издержек хранения товара.
Объем партии товара (Об) при этом равен:
143. 1000 у. д. ед. стоит 1 кг орехов или 400 г ядер. Следовательно, 1 кг ядер должен стоить в 2,5 раза (1000 г: 400 г) дороже, т. е. 2500 у. д. ед. Значит, выгоднее покупать неочищенные орехи.
144. Можно обойтись всего двумя взвешиваниями. Первое: положить на каждую чашку весов по 3 любые монеты; если монеты уравновесятся, значит, фальшивая в оставшейся тройке; если одна из чашек окажется легче – искомая монета в ней. Второе: из тройки монет, в которой обнаружена фальшивка, две любые монеты разложить по чашкам весов; если монеты уравновесятся, значит, фальшивая – оставшаяся; если одна из монет окажется легче – она и есть фальшивая. Итак, взвешивание обойдется в 200 у. д. ед.
145. Один делит пополам, второй выбирает свою часть. (Кто делит, а кто выбирает, определяется по жребию.)
146. Вначале по жребию определяется, кто будет делить (это может быть один или несколько человек). Производится раздел, который утверждается на общем собрании товарищества. Полученные части распределяются по жребию. (Описанная процедура раздела должна быть заранее одобрена всеми членами товарищества.)
147. Обозначим первоначальный капитал через х
148. 5 млн руб. и 2 млн руб.
149. 1) Поскольку общий капитал без первого предпринимателя на 50 тыс у. д. ед. больше, чем без второго, то капитал первого на 50 тыс. у. д. ед. меньше, чем второго. 2) По тем же соображениям капитал третьего предпринимателя на 50 тыс. у. д. ед. больше, чем второго. 3) Следовательно, если сложить капиталы первого, второго и третьего предпринимателей, то разница в капиталах первого и второго взаимно компенсируется и общая сумма будет равна трехкратному капиталу второго предпринимателя. 4) Но сумма капиталов первого, второго и третьего предпринимателей – это и есть общий капитал без четвертого, который, как известно, равен 750 тыс. у. д. ед. Следовательно, капитал второго предпринимателя, в соответствии с п. 3, равен 750 тыс. у. д. ед.: 3 = 250 тыс. у. д. ед. 5) Следовательно, капитал первого равен 200 тыс. у. д. ед. (на 50 тыс. у. д. ед. меньше, чем у второго), капитал третьего равен 300 тыс. у. д. ед. (на 50 тыс. у. д. ед. больше, чем у второго). 6) Поскольку, как следует из п. 1 и 2, капитал четвертого предпринимателя на 50 тыс. у. д. ед. больше, чем третьего, он равен 350 тыс. у. д. ед.
150. 1) По формуле сложных процентов (проценты на проценты) завещанный капитал (В) через С лет составит К:
где п – проценты на капитал, е – основание натурального логарифма, равное 2,731828. Подставляя в формулу соответствующие значения, получим:
С помощью таблицы сложных процентов, помещенной в приложении, получим: С = 1000 х 131,539 = 131 539 фунтов стерлингов. 2) После выделения 100 тыс. фунтов стерлингов на постройку общественных зданий останется: 131 539 - 100 000 = 31 539 фунтов стерлингов. 3) Еще через 100 лет эта сумма составит (с учетом сложных процентов): 31 539 х 131 539 = 4 147 380 фунтов стерлингов. 4) После вычета из этой суммы 3 млн фунтов стерлингов бостонским жителям достанется: 4 147 380 - 3 000 000 = 1 147 380 фунтов стерлингов. По данной формуле рассчитана таблица сложных процентов, помещенная в приложении к решениям.
151. Четыре брата и три сестры. 152. Решение данной задачи неоднозначно и зависит от толкования воли завещателя. 1) Если считать волей завещателя дать сыну наследство вдвое больше, чем матери ( 2) Если же считать волей завещателя также желание оставить матери не менее 153. Обозначив искомый процент по вкладам через х, по формуле сложных процентов (см. решение задачи 150) получим:
Логарифмируя с помощью таблицы логарифмов, получим:
Антилогарифм 1 + х = 1,042. х = 4,2 % 154. Норма процента (НП) равна:
где Д – доход, Сс – величина ссуды.
155. Величина ссуды (Сс) равна (см. решение задачи 154):
156. Величина дохода (Д) равна (см. решение задачи 154):
157. Банковская прибыль (БП) равна:
158.
159. 1) Положив деньги в банк, можно получить за год 8 тыс. руб. (8 %от 100 тыс. руб.). 2) Можно купить 4 привилегированные акции и получить 10 тыс. руб. дивидендов (10 % от 4 х 20 тыс. руб.). 3) Можно купить обыкновенные акции. Доход по ним определим исходя из следующих соображений. После первоочередной выплаты по всем привилегированным акциям 200 тыс. руб. (80 х 25 х 10 %) на выплату по обыкновенным акциям останется 800 - 200 = 600 тыс. руб. Следовательно, на каждую обыкновенную акцию придется 6 тыс. руб. дивидендов Если купить на все деньги 5 обыкновенных Следовательно, самое выгодное вложение капитала – покупка обыкновенных акций. 160. Суммарный капитал равен 150 млн руб. Прибыль на капитал равна Выплата за ссуду составит 5 млн руб. Предпринимательский доход равен 45 - 5 = 40 млн руб.
161. В соответствии с теорией статистических решений среднеожидаемая прибыль равна:
Следовательно: – при вложении капитала в кинофильм
– при вложении капитала в торговлю
Таким образом, выгоднее вкладывать капитал в торговлю.
162. При вложении денег один раз в год доход равен 150 тыс. руб. При вложении денег два раза на 6 месяцев (с учетом вложения дохода за первое полугодие) доход равен 172,25 тыс. руб. При вложении денег четыре раза на 3 месяца (с учетом вложения доходов за каждый квартал) доход равен 185,6 тыс. руб. Следовательно, выгоднее всего вкладывать деньги на 3 месяца.
163. 1) Издание книги будет безубыточным (точка безубыточности – ТБ) при тираже:
2) При цене одной книги 11 у. д. ед.:
164. Один из наиболее простых и очевидных вариантов глазомерного решения показан на рисунке а. Общая стоимость перевозки руды при этом будет составлять:
Однако методами математического планирования можно разработать значительно более экономный план перевозки руды (см. рис. б). В данном случае это можно сделать и путем простого перебора вариантов. При таком оптимальном плане общая стоимость перевозок уменьшится примерно на 25 % и составит:
165. Обозначим закупочную цену единицы товара через х. Тогда оптовая цена составит 1,2 х, розничная цена – 1,3 (1,2 х), а после ее снижения - 0,9 [1,3(1,2 х)]. По условию задачи эта последняя цена равна 100 у. д. ед., т. е. 0,9 х 1,3 х 1,2 х = 100.
166. Обозначим цену товара до и после ее снижения через х и у соответственно. Тогда условие задачи запишется так:
Из (1) следует:
Подставляя значение у в (2), получим:
167. Планируемый доход (Д) рассчитывается по формуле:
где К – количество выпущенных лотерейных билетов; Б – стоимость одного лотерейного билета; С – количество счастливых билетов; В – величина выигрыша на один счастливый билет.
Отсюда
С учетом того, что требуемый доход должен составить
При этом вероятность выигрыша на 1 билет (Рв) равна:
168. Для того чтобы Рв = 1 %, или 0,01, количество счастливых билетов С должно вырасти в десять раз и составить 9870. Тогда Д = 107 х 103 - 9870 х 10-7 = -88,7 х 109 руб. Иными словами, убыток составит около 89 млрд руб.
169. Расчет производится по формуле теории вероятностей:
где N – требуемое количество билетов, из которых хотя бы один (не менее одного) выиграет, Руд – вероятность удачи, выигрыша хотя бы одного из купленных билетов, Рв – вероятность выигрыша в лотерею на один билет.
170. Обозначая через А и П стоимости автомобиля и прицепа, получим следующие очевидные равенства:
Складывая левые и правые части равенств, получим:
Следовательно, А = 1,4 млн у. д. ед., П = 0,1 млн у. д. ед. 171. Прибыль (ПР) рассчитывается по формуле:
где В – выручка, МЗ – материальные затраты, HP – накладные расходы, ЗЗП – затраты на зарплату. Подставляя соответствующие цифры, получим: ПР = 100 000 - (50 000 + 10 000 + 10 000) = 30 000 у. д. ед. Налог на прибыль (НПР) равен 32 % от ПР, т. е. 9600 у. д. ед. Чистая прибыль (ЧПР) равна: ПР - НПР = 30 000 - 9600 = 20 400 у. д. ед. 172. Остаточная стоимость основных фондов (ОС) рассчитывается по формуле:
где ПС –первоначальная стоимость основных фондов, ПИ –процент износа основных фондов за 1 год, СИ – срок использования основных фондов. Подставляя соответствующие цифры, получим:
Прибыль от реализации основных фондов (ПРоф) рассчитывается по формуле:
где ПЦ – продажная цена основных фондов, К – индекс инфляции. Подставляя соответствующие цифры, получим:
173. 1) Общие затраты составляют: 60 + 50 + 20 + 10 = 140 у. д. ед.
Прибыль равна:
200 - 140 = 60 у. д. ед.
2) Рентабельность продукции равна:
174. На 10 000 у. д. ед. (в том числе 6000 у. д. ед. стоимость шапки и 4000 у. д. ед.– сдача). 175. Плата за кредит (Кр) рассчитывается по формуле:
где В – величина суммы кредита (первоначального вклада в Сбербанк), П – процентная ставка, С – срок кредита. Подставляя соответствующие цифры, получим:
176. По формуле сложных процентов (см. решение задачи 150) через два года вклад будет составлять:
177. По формуле сложных процентов (см. решение задачи 150) через С лет вклад будет составлять:
Логарифмируя, получим:
откуда
По приближенной формуле:
178. В первом круге операции участвует 1 покупатель, во втором – 2, в третьем – 4... в 11 круге – 1024 покупателя. Еще через 10 кругов чисто участников операции станет более миллиона, в городе не останется покупателей, и те, у кого талоны оказались нереализованными, уже нe сумеют их продать. Вот эти-то незадачливые покупатели и оплачивают разницу в цене продажи и покупки товара.
179. За 30 дней мне заплатят 30 х 100 тыс. долларов = 3 млн долларов. Я же заплачу: за 1-й день – 1 цент, за 2-й день – 2 цента, за 11-й день – 10 долларов 24 цента, за 21-й день – 10 485 долларов 76 центов, за 30-й день – 5 368 709 долларов 12 центов. За 30 дней общая сумма, которую мне придется выплатить, составит 10 737 418 долларов 3 цента, т. е. примерно в три раза больше того, то я получу.
180. Обозначим через х количество сотен тысяч рублей, указанных в чеке, а через у количество тысяч рублей, указанных в чеке. Тогда общая сумма, указанная в чеке, будет равна (х х 100 + у) тыс. руб., а сумма, выданная клиенту, – (х + l00 у) тыс. руб. Условие задачи при этом будет выглядеть так:
Преобразуя его, получим первое уравнение с двумя неизвестными:
Второе уравнение составляется исходя из следующего, не очень заметного обстоятельства, содержащегося в условии задачи: сумма в тысячах рублей, превращенная в сумму в сотнях тысяч рублей, после того как из нее вычитаются три с половиной сотни тысяч, должна при делении на число сотен тысяч (теперь это тысячи рублей) дать без остатка число 2. Вот как можно записать это условие с учетом того, что число сотен тысяч нужно, кроме трех, уменьшить еще на единицу (из которой вычитается половина сотни тысяч):
|



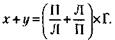

 )*.
)*.


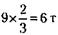 высококачественного бензина. Следовательно, в оставшемся на колонке бензине высококачественного было 24 - 6= 18 т.
высококачественного бензина. Следовательно, в оставшемся на колонке бензине высококачественного было 24 - 6= 18 т.
 высококачественного бензина. Следовательно, в оставшемся на колонке бензине высококачественного было 18 - 4= 14т.
высококачественного бензина. Следовательно, в оставшемся на колонке бензине высококачественного было 18 - 4= 14т.






 Н,
Н,




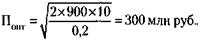




 и
и  ), а дочери – вдвое меньше, чем матери (
), а дочери – вдвое меньше, чем матери (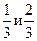 ), то наследство следует разделить в пропорции: дочери – 1 часть, матери – 2 части, сыну – 4 части, т. е.
), то наследство следует разделить в пропорции: дочери – 1 часть, матери – 2 части, сыну – 4 части, т. е. 
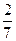 меньше
меньше  ). Тогда дочь получает
). Тогда дочь получает  , сын
, сын 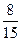 , а мать
, а мать  наследства.
наследства.


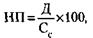





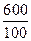 , что составляет 30 %.
, что составляет 30 %. 
 акций, то доход по ним составит 30 тыс. руб. (30 % от 100 тыс. руб.).
акций, то доход по ним составит 30 тыс. руб. (30 % от 100 тыс. руб.).