Нелинейная регрессия.
Вопросы: 5. Регрессии, нелинейные по переменным. 6. Регрессии, нелинейные по параметрам. 7. Индекс корреляции и индекс детерминации. 8. Эластичность функции.
Многие экономические зависимости не являются линейными по своей сути и их моделирование линейными регрессиями не дает положительного результата. Так для описания зависимости спроса на некоторый товар от его цены наиболее целесообразно использовать логарифмическую модель. При анализе зависимостей издержек от объема выпуска наиболее обоснованной является полиномиальная модель. Широко используемая функция Кобба-Дугласа, является степенной функцией
У – объем выпуска. К-затраты капитала. L - затраты труда. А, α, β – параметры. В современной экономике применяются также достаточно часто обратные и экспоненциальные модели. Различают регрессии нелинейные по переменным и нелинейные по параметрам.
1. К регрессиям, нелинейным по переменным относят полиномы различных степеней.:
равносторонняя гипербола функции вида Нелинейность по переменным устраняется путем замены переменной. Так в регрессии (1) сделаем замену х=х1, х2=х2 и получим двухфакторную линейную регрессию.
В уравнении (3) замена переменной имеет вид: Применение метода МНК для оценки коэффициентов соответствующих выборочной регрессии приводит к следующим системам уравнений. Для регрессии (!):
Для равносторонней гиперболы система уравнений имеет вид:
Для уравнения (4):
1. Полином третьей степени уравнения (2) часто моделирует зависимость общих издержек У от объема выпуска Х. график имеет вид:
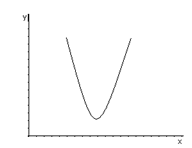
2. Полином второй степени (уравнение (1)) парабола может описать зависимость между объемом выпуска Х и средними (либо предельными) издержками У
3. Гипербола (3) (обратная модель) применяется в тех случаях, когда неограниченное увеличение объясняющей переменной Х асимптотически приближает зависимую переменную У к некоторому пределу. Если а и в - оценки параметров гиперболы соответственно, то в зависимости знаков а и в возможны следующие ситуации:
рис.1 рис.2 рис.3 График на рисунке 1 может отражать зависимость между объемом выпуска Х и средними фиксированными издержками У. график на рисунке 2 может описывать зависимость между доходом Х и спросом на блага У. Такие функции называются функциями Тронквиста. Важным приложением графика на рисунке 3 является кривая Филипса, отражающая зависимость между уровнем безработицы Х (%) и процентным изменением заработной платы У. 4. Уравнения с квадратными корнями (4) использовались в исследовании урожайности и трудоемкости с/х производства. Пример 1: На основании информации о норме безработицы и темпах инфляции (таблица 1) построить: 1. диаграмму рассеяния. 2. уравнение регрессии, описывающее зависимость темпов инфляции от нормы безработицы.
Таблица 1
Строим диаграмму рассеяния:
Из диаграммы рассеяния видно, что зависимость можно описать гиперболой
Обратимся в Excel к программе регрессия и введем данные zi,
Замечание: Для оценки коэффициентов гиперболы можно построить систему уравнений (6) и решить ее.
2. К нелинейным по параметрам регрессиям относятся: степенная: показательная экспоненциальную Нелинейные по параметрам регрессии сводятся к линейным путем логарифмирования.
(8’) (9’) (10’)
Для нахождения оценок соответствующих коэффициентов выборочных регрессии для (8’), (9’),(10’) используется МНК при условии, что Пример 2: В таблице 2 приведены данные о расходах на питание и доходах 5 групп населения. Построить степенную регрессию, описывающую зависимость расходов на питание У от доходов населения Х. Таблица 2
Степенная регрессия имеет вид:
Получим линейное уравнение. Обратимся к программе «Регрессия», введем данные столбцов v и z, получим:
Выполним обратные преобразования (пропотенцируем полученное уравнение):
Замечание: Для построения регрессии (11) можно воспользоваться формулами (8) темы 2.
3. Уравнение нелинейной регрессии также как и линейной дополняются показателями корреляции и детерминации. Для оценки тесноты связи между переменными рассчитывается индекс корреляции:
Индекс корреляции (R) меняется от 0 до 1. чем ближе R к 1, тем сильнее нелинейная связь между переменными. Величина
используется для оценки качества уравнения регрессии. Для проверки значимости индекса детерминации используется F-статистика
n – объем выборки m – число параметров при независимых переменных. Так для параболы m=2, а для степенной функции m=1 4. В экономическом анализе часто используется эластичность функции. Эластичность функции
Эластичность показывает, насколько процентов изменяется функция Для степенной функции
В примере 2 степенная регрессия Для остальных функций эластичность не является постоянной величиной. Так для линейной функции
Рассчитаем коэффициент эластичности в примере 1 темы 2:
Можно утверждать, что с увеличением расходов на новое оборудование на 1%, прибыль предприятия возрастет на 1,29%. Тема 4:
|


 (1)
(1) , (2)
, (2) , (3)
, (3) (4)
(4)
 , а в (4) -
, а в (4) -  .
. (5).
(5). (6)
(6) (7)
(7)




 . Сделаем замену переменных
. Сделаем замену переменных 
 , получим:
, получим:
 , (8)
, (8) , (9)
, (9) . (10)
. (10)
 распределен нормально.
распределен нормально.


 (11)
(11)
 (12)
(12)
 (13)
(13)
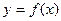 рассчитывается как относительное изменение у к относительному изменению х:
рассчитывается как относительное изменение у к относительному изменению х: (15)
(15) эластичность представляет собой постоянную величину, равную в, действительно:
эластичность представляет собой постоянную величину, равную в, действительно:
 описывает зависимость расходов на питание от доходов. Коэффициент 0,35 экономического смысла не имеет, а коэффициент в, равный 1,183, показывает, что увеличение личного дохода на 1% приведет к увеличению расходов на питание в среднем на 1,183%.
описывает зависимость расходов на питание от доходов. Коэффициент 0,35 экономического смысла не имеет, а коэффициент в, равный 1,183, показывает, что увеличение личного дохода на 1% приведет к увеличению расходов на питание в среднем на 1,183%. эластичность
эластичность  , т.е. эластичность зависит от х, поэтому для остальных функций вычисляется средний показатель эластичности, в частности для линейной функции по формуле:
, т.е. эластичность зависит от х, поэтому для остальных функций вычисляется средний показатель эластичности, в частности для линейной функции по формуле: (16)
(16)



