Абсолютная и относительная погрешности прямых измерений
Результат измерения величины Х должен быть представлен в виде: Х =
где Xi – значения, полученные в результате отдельных измерений, N – число измерений. Среднее значение
В общую погрешность измерений вносят вклад систематические и случайные погрешности. Если обозначить систематическую погрешность измерения буквой δ, а случайную погрешность – d, то общая погрешность DХ определится по формуле:
Существует несколько способов определения систематической погрешности: 1) правило половины деления. Если на измерительном приборе не указана погрешность его измерений, то в качестве таковой надо взять половину деления шкалы прибора; 2) определение погрешности по классу точности прибора. На многих приборах обозначен их класс точности, он показывает долю от максимального значения шкалы прибора, выраженную в процентах, которую нужно взять для того чтобы получить значение систематической погрешности; 3) на некоторых приборах систематическая погрешность указана непосредственно. Допустим, что основной вклад в погрешность измерений даёт случайная погрешность, тогда с помощью методов математической статистики можно уменьшить доверительный интервал для истинного значения измеряемой величины. Для этого нужно провести некоторое количество повторных измерений и рассчитать доверительный интервал по нижеприведённым формулам. Чем больше будет сделано повторных измерений, тем меньше окажется абсолютная погрешность и соответствующий ей доверительный интервал. Прежде всего, определим дисперсию выборки
где DХi – отклонения от среднего результатов единичных измерений DХi = Хi –
Стандартным отклонением (или среднеквадратичной погрешностью) SX отдельного измерения величины Х называется квадратный корень из дисперсии:
Оценка стандартного отклонения среднего значения величины Х (от истинного значения μ)
Эта формула показывает, что выборочное стандартное отклонение среднего значения величины Х уменьшается с увеличением числа измерений. Важно уловить разницу между Погрешность измерения величины Х определяется согласно формуле:
DХ = kα,N×
В этой формуле величина kα,N называется коэффициентом Стьюдента. Его значение зависит от числа измерений и вероятности попадания истинного значения μ величины Х в доверительный интервал
Таблица 2.1
|

 ± DХ, где
± DХ, где  , (2.3)
, (2.3)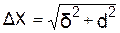 . (2.4)
. (2.4) измеряемой величины Х с помощью формулы:
измеряемой величины Х с помощью формулы: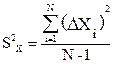 , (2.5)
, (2.5) . (2.6)
. (2.6)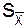 даётся формулой:
даётся формулой: . (2.7)
. (2.7)


