ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Общие положения Жидкости и газы по своим механическим свойствам очень похожи. Поэтому их часто рассматривают и описывают одинаково, считая сплошными средами, не имеющими структуры. Но если обратиться к молекулярному устройству жидкостей и газов, то станут очевидными различия, связанные с разным положением молекул в них. В жидкостях расстояние между молекулами гораздо меньше, чем в газах, молекулы «упакованы» значительно плотнее, поэтому имеют место некоторые особенности. Одна из таких особенностей – явление поверхностного натяжения, которое рассматривается в данной лабораторной работе. Явление поверхностного натяжения заключается в стремлении жидкости сократить площадь своей поверхности. Это явление можно объяснить, основываясь на представлениях о молекулярном строении жидкостей. На каждую молекулу жидкости со стороны других молекул действуют силы гравитационного притяжения:
где G = 6,6725´10-11 м3/(кг×с2) – гравитационная постоянная, m 1, m 2 – массы взаимодействующих молекул; R – расстояние между центрами их масс. Как видно из (1), силы притяжения между молекулами очень быстро убывают с расстоянием (обратно пропорционально квадрату расстояния между ними). Поэтому, начиная с некоторого «граничного» расстояния этими силами можно пренебречь. Это расстояние имеет величину порядка 10-9 м и называется радиусом молекулярного действия r. Сфера радиуса r называется сферой молекулярного действия. Итак, каждая молекула подвергается действию сил притяжения со стороны молекул, входящих в сферу молекулярного действия. Но молекулы, находящиеся за пределами этой сферы, не действуют на рассматриваемую молекулу (точнее, действием сил притяжения к ним можно пренебречь). Выделим некоторую молекулу жидкости, окруженную со всех сторон другими молекулами. Силы, действующие на нее, сосредоточатся внутри сферы молекулярного действия (рис. 1). Эти силы направлены в разные стороны. А так как количество молекул внутри сферы молекулярного действия очень велико[1], то силы притяжения рассматриваемой молекулы к ним в целом скомпенсированы, и равнодействующая всех этих сил равна нулю (в этом можно легко убедиться на рис. 1: возьмите любую молекулу внутри сферы молекулярного действия и найдите вторую молекулу, расположенную на таком же расстоянии, но с противоположной стороны от рассматриваемой молекулы).
Рис. 1. Силы, действующие на молекулу, находящуюся в объеме жидкости:
Таким образом, молекула, находящаяся в объеме жидкости не испытывает на себе воздействия со стороны других молекул, так как их суммарное воздействие на рассматриваемую молекулу скомпенсировано. Совершенно иная картина по сравнению с глубиной жидкости наблюдается на её поверхности. Здесь на любую рассматриваемую молекулу так же будут действовать силы со стороны молекул жидкости, находящихся внутри сферы молекулярного действия. Коренное различие заключается в том, что жидкость находится только с одной стороны от поверхности. С другой стороны находится газ или вакуум. Как уже было отмечено выше, расстояние между молекулами в газе значительно (на несколько порядков) превышает расстояние между молекулами в жидкости. Это означает, что количество молекул газа, находящихся вблизи границы раздела жидкость – газ и могущих притягивать рассматриваемую молекулу, несущественно и их воздействием мы вправе пренебречь. Следовательно, сфера молекулярного действия превращается в полусферу, и равнодействующая молекулярных сил уже не будет равна нулю. Эта равнодействующая направлена внутрь жидкости и в общем случае не перпендикулярна и не параллельна поверхности жидкости (рис. 2).
Рис. 2. Силы, действующие на молекулу, находящуюся на границе раздела фаз жидкость – газ:
Для того чтобы найти равнодействующую всех сил, действующих на рассматриваемую молекулу на поверхности жидкости, необходимо сложить силы, с которыми рассматриваемая молекула притягивается к каждой молекуле, входящей в сферу молекулярного действия. Для этого каждую такую силу следует представить в виде двух ортогональных составляющих: нормальную к поверхности жидкости и касательную к ней (рис. 3).
Рис. 3. Силы поверхностного натяжения и внутреннего (молекулярного) давления жидкости:
Первая – нормальная к поверхности сила Fд – вызывает так называемое внутреннее, или молекулярное давление – давление жидкости на себя. Это давление не действует на тела, помещенные в жидкость, ибо оно вызвано исключительно молекулярными силами. Вторая же сила – касательная к поверхности FП . Н – называется силой поверхностного натяжения. Эта сила всегда стремится сократить свободную поверхность жидкости. Если мы будем каким-либо способом растягивать поверхность, силы поверхностного натяжения будут препятствовать этому. Рассмотрим этот процесс с энергетической точки зрения. Чтобы развести две молекулы на некоторое расстояние, необходимо совершить работу против сил молекулярного притяжения (1). Это означает, что система из многих молекул будет обладать потенциальной энергией вследствие межмолекулярного взаимодействия. Во внутренних слоях жидкости, как мы помним, молекулярные силы скомпенсированы (то есть их равнодействующая равна 0), поэтому потенциальная энергия отсутствует (равна 0). В поверхностном слое это не имеет места; молекулы поверхностного слоя обладают потенциальной энергией из-за существования нескомпенсированной силы поверхностного натяжения. Эта потенциальная энергия называется поверхностной энергией. Чтобы увеличить площадь свободной поверхности, необходимо совершить работу против сил поверхностного натяжения. Энергия, затраченная при этом, превращается в поверхностную энергию, которая таким образом увеличивается. Если теперь прекратить воздействие на жидкость, она, в соответствии с принципом минимума энергии, сократит свою поверхность до минимально возможного в данных условиях значения. Совершенно очевидно, что изменение поверхностной энергии ΔE в этом случае будет пропорционально изменению площади свободной поверхности жидкости ΔS:
ΔE = a ΔS. (2) Коэффициент пропорциональности a в (2) называется коэффициентом поверхностного натяжения жидкости. Так как для изменения поверхностной энергии необходимо совершить работу (A = ΔE), то из уравнения (2) можно получить следующее соотношение, определяющее физический смысл коэффициента поверхностного натяжения:
Как видно из формулы (3), коэффициент поверхностного натяжения численно равен работе, совершенной молекулярными силами при изменении площади свободной поверхности жидкости на 1 м2 при постоянной температуре. Если выделить в свободной поверхности жидкости некоторый замкнутый контур, то сила поверхностного натяжения, приведенная к единице длины этого контура, также будет численно равна коэффициенту поверхностного натяжения:
Исходя из формул (3) и (4), можно определить размерность коэффициента поверхностного натяжения. В СИ он обычно измеряется в ньютонах на метр (Н/м) или в джоулях на квадратный метр (Дж/м2). Иногда используется также единица системы СГС дина на сантиметр (дин/см), равная 10-3 Н/м. Величина поверхностного натяжения зависит от температуры – с ростом температуры она уменьшается. Также в значительной степени она зависит от примесей, содержащихся в жидкости. Существуют различные методы определения коэффициента поверхностного натяжения. Ниже изложены теоретические основы некоторых из них.
|

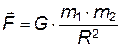 , (1)
, (1)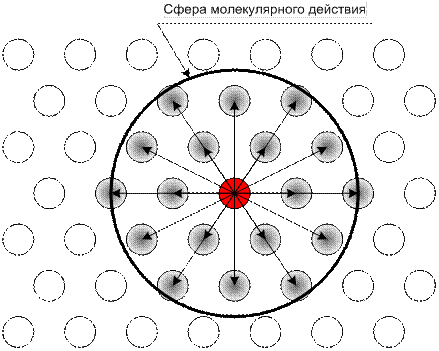
 – рассматриваемая молекула;
– рассматриваемая молекула;  – молекулы, входящие в сферу молекулярного действия;
– молекулы, входящие в сферу молекулярного действия;  – молекулы, не входящие в сферу молекулярного действия;
– молекулы, не входящие в сферу молекулярного действия;  – силы притяжения, действующие на рассматриваемую молекулу
– силы притяжения, действующие на рассматриваемую молекулу
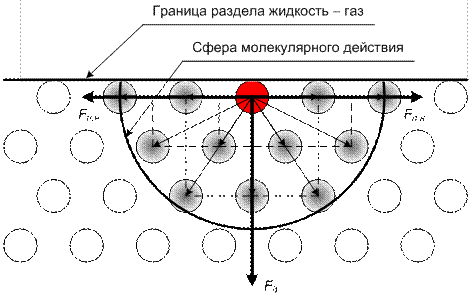
 – сила поверхностного натяжения;
– сила поверхностного натяжения;  – сила, обуславливающая внутреннее (молекулярное) давление
– сила, обуславливающая внутреннее (молекулярное) давление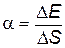 . (3)
. (3)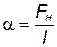 . (4)
. (4)


