Пермь 2004
Составитель: Р.Я.Газизов
УДК 539.3
Методическое пособие по курсу «Ресурс и надежность изделий из композиционных материалов»./ Сост.:Р.Я.Газизов. Перм. гос. техн. ун-т, Пермь, 2004 – 45с.
В методическом пособии приведены примеры решения задач по основным разделам курса, условия задач, большой объем справочной информации. Пособие рекомендуется для самостоятельных занятий.
Табл. 12, ил. 10.
Рецензент д.т.н. А.Н.Аношкин
Пермский государственный технический университет,2004
Определение напряжений и деформаций. Пример. 1. Стержень длиной 25см и диаметром 0,25 см растягивается нагрузкой 4500 Н. Диаметр стержня уменьшился до величины 0,22 см. Рассчитаем следующие параметры. а. Конечную длину стержня: Поскольку
б. Истинные напряжение и деформацию при заданной нагрузке:
в. Относительные напряжение и деформацию при заданной нагрузке:
Использование значений истинных деформаций при рассмотрении пластической деформации, проходящей без изменения объема тела, не только лучше характеризует саму пластичность, но и удобно, так как при этом
1. К стержню длиной 200 мм и диаметром 2,5 мм подвешивают груз 2000 Н. При условии, что диаметр стержня уменьшился до 2,2 мм, рассчитать следующие величины: а) окончательную длину стержня; б) истинные напряжения и деформации при такой нагрузке; в) относительные напряжения и деформации при такой нагрузке.
2. Круглый стержень диаметром 1,28 см и длиной 5 см из катаной стали марки 1080 растягивается до разрушения. Какова необходимая для разрушения стержня нагрузка? Если 80% от общего удлинения есть равномерное удлинение (без локализации деформации), рассчитать истинные напряжения в точке зарождения шейки.
3. Платформа подвешена на двух параллельных стержнях как показано на рисунке: каждый стержень имеет диаметр 1,28 см. Стержень А изготовлен из стали марки 4340 после закалки и отпуска при 650 ºС (Е = 210 ГПа,
а) какая однородная нагрузка может быть приложена к платформе, чтобы при этом не возникло пластическое течение? б) какой из стержней начнет пластически деформироваться раньше? Примечание: оба стержня испытывают одинаковую упругую деформацию.
4. Стержень длиной 100 мм из стали 1340 после закалки и отпуска при 205 °С нагружается силой 50000 Н. Если диаметр стержня 10 мм, то какая деформация в нем возникнет? Какая деформация останется, если снять нагрузку?
5. Образец на растяжение из отожженной стали (Е = 210 ГПа, σт = 425 МПа) имеет минимальный диаметр 1,28 см и длину рабочей части 5 см. Максимальная нагрузка равна 66700 Н, разрушение наступает при нагрузке 44500 Н: а) какова прочность материала на растяжение? б) почему разрушение наступает при нагрузке более низкой, чем максимальная? в) как выглядит рабочая часть образца в момент перед разрушением? г) рассчитать деформацию и описать ее характер при растягивающем напряжении 100 МПа.
6. Круглый стержень длиной 5 см и диаметром 1,28 см из катаной стали 1015 нагружается растяжением до разрушения: а) какова должна была быть нагрузка для разрушения образца? б) если 60% от общей деформации пришлось на равномерную (т. е. до образования участка локальной деформации), то рассчитать истинные напряжения в точке зарождения шейки.
7. Образец диаметром 0,25 см и длиной 2,5 см равномерно растягивается до 3 см, после чего начинается локализация деформации в шейке под нагрузкой 1400 Н. Рассчитать относительные и истинные напряжения и деформации в момент образования шейки.
8. Образец закладывается в машину для испытаний на ползучесть и нагружается усилием 5000 Н. Начальная длина круглого стержня составляла 200 мм, исходный диаметр 5 мм. После нескольких сотен часов испытаний длина образца стала 230 мм: а) каким в этот момент оказался диаметр образца? б) какими были истинная и относительная деформации в этот момент? в) какими были истинное и относительное напряжение в этот момент? г) если испытания проводились при условии постоянства истинных напряжений, то изменилась бы или нет нагрузка на образец, и если да, то насколько?
Разрушение конструкционных материалов 9. Для определенного конструкционного сплава обнаружено, что прочность при растяжении образцов с надрезом уменьшается при увеличении глубины надреза притом, что радиус в вершине надреза остается постоянным до значения, выше которого
10. Для большинства конфигураций, показанных на рис.1, при отношении величины радиуса в вершине надреза к минимальному диаметру, стремящемуся к нулю, 11. 15 января 1919 г. на Коммершиал стрит в Бостоне произошло ужасное событие. Гигантский резервуар диаметром 27 м и высотой 15 м внезапно разрушился, и более чем 7,5·106 л мелассы (черной патоки) хлынуло на улицы. Сообщают, что без каких-либо предварительных признаков предстоящей катастрофы верхняя часть резервуара взлетела в воздух, а стенки лопнули и разошлись в стороны. Находящееся по соседству городское здание, в котором в это время завтракали служащие, было разрушено и под ним были погребены люди. Частью резервуара было разрушено здание пожарной охраны и при этом также были убиты и ранены несколько пожарников. В результате разрушения стенка резервуара наткнулась на одну из колонн, поддерживающих подъемник, принадлежащий фирме «Boston Elevated Railway Co.». Колонна полностью расщепилась и ушла вниз под конструкцию. В результате пути оказались разрушенными и вся конструкция опустилась вниз на несколько футов. Двенадцать человек погибли, утонув в мелассе, задохнувшись или попав под обломки. Еще более сорока человек оказались ранеными. Многие лошади, принадлежащие муниципальным органам управления, утонули, а других пришлось пристреливать. Мог ли уцелеть резервуар с мелассой, если бы он был воздвигнут в тропиках?
12. Было показано, что тщательно приготовленные прутки из кремня могут выдерживать до разрушения воздействие чрезвычайно высоких напряжений. Когда же разрушение происходит, образец рассыпается в порошок. Почему?
Пример 2. Трещина, исходящая от круглого отверстия. Эта конфигурация (рис.3, а) часто встречается на практике, особенно в авиационных деталях, содержащих множество отверстий под заклепки; трещина часто исходит изэтих областей, характеризующихся высокой концентрацией напряжений. Для случая круглого отверстия
Как и следовало ожидать, параметр К быстро уменьшается при увеличении L, так как с ростом L трещина уходит из области высокой концентрации напряжений. Поэтому уравнение (1) представляет собой верхнее граничное решение для трещины указанной конфигурации. Нижнее граничное решение можно получить из условия L>R. Длина трещины составляет L+2R. Отсюда:
Верхние и нижние граничные решения для нескольких значений отношения L/R приведены в табл.1. Кроме того, в табл.1 приведены поправочные коэффициенты F(L/R) для трещины рассматриваемой конфигурации, основанные на предложенном Бови решении, согласно которому:
K=F(L/R)
Следует отметить очень хорошее соответствие между уравнениями (1) и (2) для двух экстремальных случаев: L / R = 0 и L/R>
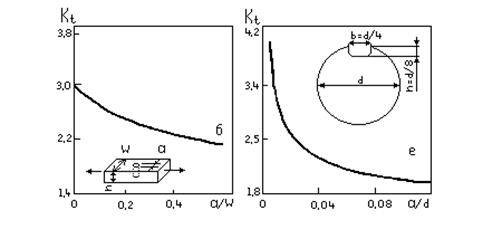
Рис.1. Влияние геометрии сечения на коэффициент концентрации напряжения. а) осевое нагружение прутка с надрезом; б) осевое нагружение прутка с углублением; в) изгиб прутка с надрезом; г) изгиб вала с поперечным отверстием; д) осевое нагружение прутка с поперечным отверстием; е) кручение прямого участка вала со шпоночным пазом; цифры у кривых – отношение D/d
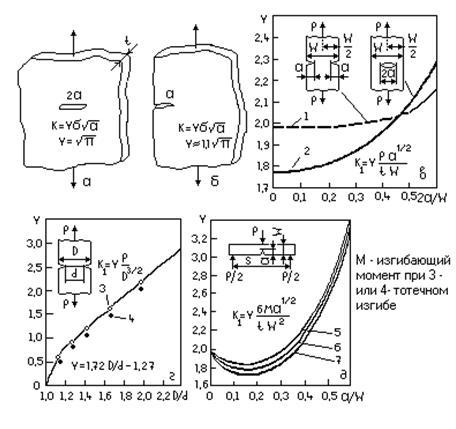
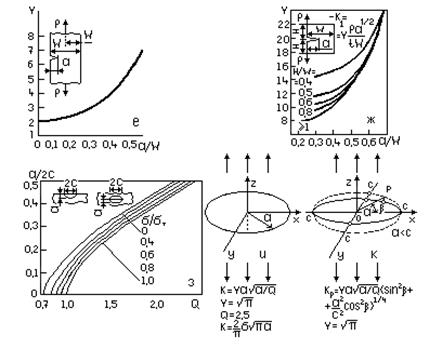
Рис.2. Коэффициент интенсивности напряжений для образцов различных форм и размеров (а – к), кривые 1-6 S/W=8; 7-то же, при S/W=4
Рис. 3. Сложные конфигурации трещин: а— трещина, исходящая из отверстия; б —полукруглая угловая трещина; в —эллиптическая угловая трещина, исходящая от отверстия, высверленного по толщине
Пример 3. Полукруглая круговая трещина. Эта конфигурация (рис.3,б) описывается геометрическими размерами, представленными на рис.2,б,и. В связи с тем, что трещина круглая и расположена вдоль двух свободных поверхностей, доминирующий уровень интенсивности напряжений можно аппроксимировать выражением:
где (1,12)
Пример 4. Эллиптическая угловая трещина, растущая от одного угла через отверстие по толщине. Анализ трещины указанной конфигурации (рис.3,в) включает многие факторы, рассмотренные в двух предыдущих примерах, а также некоторые конфигурации, показанные на рис.2. Максимальная интенсивность напряжений в этом примере реализуется в точке А, т.к. в этом месте трещина находится под воздействием максимально сконцентрированных напряжений, связанных с наличием отверстия, а также и потому, что точка А расположена при Для приближенного решения предлагается выражение:
где
Пример 5. Стальная пластина с центральным дефектом по толщине длиной 16 мм подвергается воздействию напряжения величиной 350 МПа, направленного по нормали к плоскости трещины. Каковы будут размер пластической зоны и уровень эффективной интенсивности напряжения в области вершины трещины, если предел текучести материала составляет 1400 МПа? Принимая, что пластина бесконечно большая, rу можно определить
из уравнений
rу = (1/2p) [З502p(0,008)/14002] =0,25мм. В связи с тем, что величина отношения rу /а очень мала, не следует ожидать, что К
т. е. лишь на 2% больше,чем Если же взять вторую стальную пластину с трещиной таких же размеров и приложенным напряжением той же величины, и подвергнутьее термической обработке, обусловливающей получение предела текучести 385 МПа, то поправка, связанная с зоной пластической деформации, будет значительно больше. Размер зоны пластической деформации будет определяться уравнением:
т. е. размер зоны пластической деформации составит уже 1/5 от полной длины и будет значительно больше:
что соответствует поправке 30%. Когда расчетная величина зоны пластической деформации составляет значительную долю от действительной длины трещины и поправка к значению интенсивности напряжений велика, процедура приблизительного использования поправочного коэффициента не всегда правомочна. Когда такая большая поправка используется применительно к упругим напряжениям, приближения, связанные с полем упругих напряжений, начинают играть менее важную роль. Пример 6. Предположим, что надо изготовить деталь в форме большого листа из стали типа 4340, содержащей 0,45% С, и соответствующие добавки Mi, Сг и Мо. Требуется, чтобы критический размер дефекта был более 3 мм, т. е. более предельной величины разрешения допустимых дефектов существующими методами неразрушающего контроля. Заданный расчетный уровень напряжений составляет половину от величины предела текучести. Для экономии массы было предложено увеличить предел текучести материала от 1520 до 2070 МПа. Допустимо ли такое увеличение прочности? При проведении всех расчетов принимается, что соблюдаются условия плоскодеформированного состояния.
Ответ на этот вопрос во многом зависит от изменения вязкости разрушения материала, связанного с увеличением предела текучести. Было показано, что при уровне прочности 1520 МПа величина K1c составляет 66 МПа Исходя из изложенного, невозможно, увеличивая прочность сплава до 2070 МПа, одновременно уменьшить массу конструкции, так как мы не удовлетворяем выдвигаемым требованиям к минимальному размеру дефекта. Более того, базируясь на допустимом размере дефекта, равном 4,8 мм (т. е. прочности 1520 МПа), при переходе к прочности 2070 МПа можно показать, что уровень расчетных напряжений необходимо снизить с 1035 до 380 МПа, а именно Пример 7. Пластина из сплава Zeusalloy 100 (сталь с пределом текучести 415 МПа) имеет величину K1c = 132 МПа
Вы поступите правильно, если примете конфигурацию центральной трещины такой, чтобы можно было использовать уравнение (6), однако ошибетесь, если подставите в это уравнение величину K1c = 132 МПа
Пример 8. В аллюминиевой панели шириной b = 2 м и толщиной h = 100 мм обнаружена плоская сквозная трещина в сварном шве. Панель нагружена усилием F = 1400 тс, трещина длиной Длина трещины мала по сравнению с шириной панели. Коэффициент интенсивности напряжений вычислим по формуле
Прежде чем подставить конкретные числовые значения в (7), переведем все данные в систему СИ. Сила F = 1400 тс =
Формула (7) дает
т.е. критическая длина трещины
Пример 9. Поперечная трещина длиной Проверку можно провести двумя способами: 1) Вычислим 2)Посчитаем критическую длину дефекта по формуле (7):
т.е. длина имеющейся трещины почти в 20 раз меньше критической длины. Посмотрим теперь, как следует учитывать конечные размеры детали и вводить поправку на пластическую зону у вершины трещины. Для учета реальной геометрии тела из таблицы 8 мы берем соответствующий К - тарировочный множитель Y, например, для полосы шириной b с боковым надрезом длины
где
а Вернемся к разобранному примеру 9 о крановой балке и предположим на этот раз, что 1) поперечная трещина в нижней полке расположена не в середине балки, а с краю, 2) кран должен работать на открытом воздухе, а по сводке погоды во время работы ночной смены температура может упасть до нуля градусов. Из справочника находим, что при такой температуре вязкость разрушения снизится до В данном примере относительная глубина трещины
Вычислим по формуле (6) поправку Ирвина на пластичность
Снова проверим безопасность балки двумя способами 1) (вспомните, что ночью вязкость разрушения стали может понизиться до 60 МПа 2) (вспомните, что в балке обнаружена трещина длиной Усталостную долговечность предсказывать сложнее, но не намного. Для описания роста усталостной трещины чаще всего используется закон Париса. С помощью формулы (8) выразим размах изменения коэффициента интенсивности за цикл нагружения
где
и проинтегрировать
Из критерия хрупкого разрушения В общем случае Y зависит от
Пример 10. На рис.а показан в двух проекциях растягиваемый длинный образец прямоугольного поперечного сечения, содержащий налоненный под некоторым углом трещиноподобный надрез. Длина надреза 2
сравнению с шириной b и толщиной t образца. Используя ЛМР, требуется определить значение растягивающего напряжения на удаленной границе, при котором трещина начинает расти. Положим Приведем напряженное состояние вдали от трещины к плоскости, параллельной плоскости надреза (предполагая, что трещина начнет развиваться в некоторой точке внутри образца); нормальные и касательные напряжения при этом (см. рис. б) будут равны
Найдем следующие выражения для коэффициентов интенсивности напряжений:
В случае, когда
Из которого имеем
Для указанных выше численных значений параметров получаем
что очень близко к тому, которое получается для трещины, перпендикулярной направлению растяжения (200 МПа).
13. Конструкция и метод испытания компактного образца на внецентренное растяжение H/W = 0,6, оговорены методикой ASTM Е-399-72. В соответствии с этим была получена кривая I-го типа в координатах нагрузка-смещение [ Р = ƒ(σ) ] и были определены максимальная нагрузка
14. Бесконечно большой лист подвергнут воздействию напряжения величиной 350 МПа. В листе расположена центральная трещина длиной 5/π см, а предел текучести материала составляет 500 МПа. а. Рассчитайте величину коэффициента интенсивности напряжений области вершины трещины. б. Рассчитайте размер зоны пластической деформации в области вершины трещины. в. Прокомментируйте надежность поправочного коэффициента к этой пластической зоне для рассмотренного случая.
15. Острая дискообразная трещина диаметром 2,5 см полностью расположена в твердом теле. Катастрофическое разрушение происходит после приложения напряжения 700 МПа. а. Какова вязкость разрушения материала? Рассмотрите случай плоскодеформированного состояния. б. Если лист из этого материала толщиной 0,75 см подготовлен для проведения испытаний на вязкость разрушения (t = 0,75, a = 3,75 см), то будет ли полученная величина вязкости разрушения надежной, если предел текучести материала составляет 1100 МПа? в. Какова должна быть толщина листа для получения надежной величины K1c ?
16. Для результатов испытаний сплава Ti—6% Al—4% V, приведенных в табл. 4 (приложения), определите размеры наибольших поверхностных дефектов эллиптической формы (а/2с
17. Для того же материала и расчетного напряжения, что и в задаче 16, рассчитайте толщину стенки баллона, содержавшего дефект эллиптической формы (a/2с
18. Вам предоставляется возможность заработать 10 млн. дол. за то, что Вы провисите на тросе в течение 1 мин. Трос прикреплен к стеклянному листу 300 см длиной, 10 см шириной и 0,127 см толщиной. Ситуация осложнена следующими факторами: а.) стеклянный лист содержит центральную трещину общей длиной 1,62 см, направленную параллельно земле; вязкость разрушения стекла составляет 0,83 МПа б.) трос подвешен на высоте 3 м над ямой с ядовитыми змеями. Попытаете ли Вы счастья? 19. Необходимо изготовить крупную панель из материала, характеризующегося величиной вязкости разрушения в условиях плоскодеформированного состояния, равной 50 МПа а.) В случае если панель подвергается воздействию напряжения 250 МПа, каким будет максимальный размер допустимого дефекта до начала катастрофического разрушения? Примите какую-нибудь конфигурацию центрального надреза; б.) Каким будет размер зоны пластической деформации в центральной части панели вдоль фронта трещины в момент разрушения? в.) Будут ли надежно соблюдаться условия плоскодеформированного состояния, если толщина панели составляет 2,5 см? г.) Будет ли изменяться критический размер дефекта, рассчитанный в п. а, если толщина панели увеличится до 10 см?
20. Тонкая листовая рессора испытывает простой изгиб в одном направлении и на растягиваемой поверхности образуется полуэллиптический дефект а/2с = 0,15. Как и следовало ожидать, плоскость расположения дефекта ориентирована нормально по отношению к направлению изгибающего напряжения. Повторяющееся нагружение обусловливает развитие трещины. Определите, будет ли изменяться (увеличиваться или уменьшаться) степень эллиптичности (а/2с)?
21. Рассчитайте максимальный допустимый радиус полукруглого поверхностного дефекта в алюминиевом сплаве 7075-Т651, подвергнутого нагружению с созданием напряжений 240 МПа в L-T, T-L и S-L направлениях. Примите условие плоскодеформированного состояния. (см. Табл.5,6 Приложений, Рис. 7)
22. Экструдированный пруток диаметром 8 см из алюминиевого сплава 7178-Т651 надо обработать, получив из него стакан с внутренним диаметром 7 см. Рассчитайте размер наибольшего допустимого поверхностного дефекта полукруглой формы, ориентированного вдоль оси стакана, при наличии которого последний будет выдерживать давление жидкости 50 МПа, создаваемое в результате воздействия поршня на жидкость, налитую в выточенный стакан.
23. Два образца с надрезом вырезали из горячекатаного стального листа в соответствии с раскроем, показанным на рисунке: а) Приняв, что ширина образцов велика по сравнению с острой трещиной, длиной 2,5 см, рассчитайте вязкость разрушения образцов А и Б, если напряжение при разрушении образцов составляет соответственно 325 и 260 МПа.
б) В чем причина различной вязкости образцов? в) Что можно предпринять для повышения вязкости материала, испытываемого так, как образец Б?
24. Вас попросили определить K1c материала, поставляемого в виде экструдированного прутка. Сравните величины K1c , полученные при испытании длинных образцов на изгиб, компактных дискообразных образцов и коротких образцов.
25 Надо изготовить деталь прямоугольной формы из самой дешевой стали, например из стали с минимальным содержанием легирующих э
|

 (постоянство объема), то
(постоянство объема), то см
см МПа,
МПа, ln
ln 
 МПа,
МПа, %
% Для относительных деформаций выражение, напротив, не столь удобно:
Для относительных деформаций выражение, напротив, не столь удобно: 
 = 855 МПа); стержень В изготовлен из алюминиевого сплава 7075-Т6 (Е = 70 ГПа,
= 855 МПа); стержень В изготовлен из алюминиевого сплава 7075-Т6 (Е = 70 ГПа, 
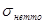 начинает возрастать. Объясните это?
начинает возрастать. Объясните это? возрастает до бесконечности. В реальных условиях такие высокие значения
возрастает до бесконечности. В реальных условиях такие высокие значения  трещины расположена в локальной области концентрации напряжений и трещину можно рассматривать как мелкий поверхностный дефект. Коэффициент интенсивности напряжений определяется уравнением:
трещины расположена в локальной области концентрации напряжений и трещину можно рассматривать как мелкий поверхностный дефект. Коэффициент интенсивности напряжений определяется уравнением: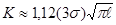 (L<<R). (1)
(L<<R). (1)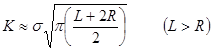 (2)
(2)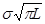 . (3)
. (3) .
.


 , (4)
, (4) - поправка, учитывающая влияние двух поверхностей дефекта;
- поправка, учитывающая влияние двух поверхностей дефекта;  -поправка, учитывающая своеобразную конфигурацию трещины (в форме монеты).
-поправка, учитывающая своеобразную конфигурацию трещины (в форме монеты). = 90
= 90  (см. рис.2,к).
(см. рис.2,к). , (5)
, (5) -параметр, характеризующий максимальную интенсивность напряжений вдоль эллиптической поверхности в точке А;
-параметр, характеризующий максимальную интенсивность напряжений вдоль эллиптической поверхности в точке А;  - глубина дефекта эллиптической формы;
- глубина дефекта эллиптической формы;  -половина ширины дефекта эллиптической формы;
-половина ширины дефекта эллиптической формы;  - толщина пластины; 1,12-поправка, учитывающая поверхностный дефект в точке А; 3
- толщина пластины; 1,12-поправка, учитывающая поверхностный дефект в точке А; 3  -параметр, учитывающий влияние концентрации напряжений в точке А; Q - поправка на дефект эллиптической формы [Q = f(a/2c)];
-параметр, учитывающий влияние концентрации напряжений в точке А; Q - поправка на дефект эллиптической формы [Q = f(a/2c)];  - поправка на конечную толщину плиты, учитывающая относительно большую величину отношения a/t (рис 2.к).
- поправка на конечную толщину плиты, учитывающая относительно большую величину отношения a/t (рис 2.к). (6)
(6) будет существенно превышать
будет существенно превышать  . Действительно:
. Действительно: =
=  =56,4 МПа
=56,4 МПа  ,
, мм,
мм, МПа·
МПа·  ,
, , 2а = 4,8мм, что удовлетворяет конструктора, так как превышает требования, выдвигаемые к минимальному размеру дефекта, выявляемого существующими методами контроля. Однако при уровне прочности 2070 МПа, 33 МПа
, 2а = 4,8мм, что удовлетворяет конструктора, так как превышает требования, выдвигаемые к минимальному размеру дефекта, выявляемого существующими методами контроля. Однако при уровне прочности 2070 МПа, 33 МПа  =380 МПа. Таким образом, при одинаковом допустимом размере дефекта (4,8 мм) уровень допустимых напряжений в более прочном сплаве может составлять лишь половину от того, который можно допустить в менее прочном сплаве, что определяет двукратное увеличение массы детали.
=380 МПа. Таким образом, при одинаковом допустимом размере дефекта (4,8 мм) уровень допустимых напряжений в более прочном сплаве может составлять лишь половину от того, который можно допустить в менее прочном сплаве, что определяет двукратное увеличение массы детали. для сплава Zeusalloy 100 возможно в случае наличия зависимости вязкости разрушения от толщины пластины. Кроме того, можно оценить величину К
для сплава Zeusalloy 100 возможно в случае наличия зависимости вязкости разрушения от толщины пластины. Кроме того, можно оценить величину К  =
=  (1+1,4
(1+1,4  ), где β1c = (l/t)(K1c/σt)2; t—толщина.
), где β1c = (l/t)(K1c/σt)2; t—толщина. . Критерий хрупкого разрушения
. Критерий хрупкого разрушения  определяет критический размер трещины:
определяет критический размер трещины: (7)
(7)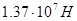 , напряжение
, напряжение .
.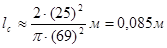 ,
, , так что имеющаяся трещина длиной
, так что имеющаяся трещина длиной  МПа. Является ли эксплуатация безопасной, если вязкость разрушения стали
МПа. Является ли эксплуатация безопасной, если вязкость разрушения стали 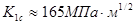 ?
? . Сравним найденное значение с вязкостью разрушения. Поскольку
. Сравним найденное значение с вязкостью разрушения. Поскольку 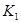 много меньше
много меньше 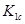 , балку считаем совершенно безопасной, разумеется, с упомянутыми в примере (8) оговорками.
, балку считаем совершенно безопасной, разумеется, с упомянутыми в примере (8) оговорками.
 , (8)
, (8) ,
, - относительная глубина нареза. Формула (8) дает хорошую точность вплоть до
- относительная глубина нареза. Формула (8) дает хорошую точность вплоть до 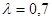 . Поправка Ирвина на пластичность материала заключается в фиктивном увеличении длины трещины на малую величину, которая приблизительно равна радиусу пластической зоны у вершины трещины.
. Поправка Ирвина на пластичность материала заключается в фиктивном увеличении длины трещины на малую величину, которая приблизительно равна радиусу пластической зоны у вершины трещины. , а предел текучести - до 480
, а предел текучести - до 480 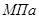 .
. , для такой глубины К – тарировочный множитель Y по таблице 8 равен
, для такой глубины К – тарировочный множитель Y по таблице 8 равен



 ниже минимальной рабочей температуры.
ниже минимальной рабочей температуры. (9)
(9) - размах изменения напряжений за цикл нагружения. Для нахождения зависимости
- размах изменения напряжений за цикл нагружения. Для нахождения зависимости  :
:
 . (10)
. (10) находим критическую длину
находим критическую длину 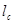 , а долговечность
, а долговечность  получиться при подстановке
получиться при подстановке  (11)
(11)




 таково, что наибольшую роль играет
таково, что наибольшую роль играет 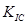 , можно получить условие перехода в критическое состояние
, можно получить условие перехода в критическое состояние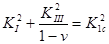 .
.
 ,
,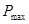 и величина критической нагрузки P
и величина критической нагрузки P  . При размерах образца W = 10 см, t = 5 см и a = 5 см величины критической нагрузки и максимальной нагрузки составили соответственно: Р
. При размерах образца W = 10 см, t = 5 см и a = 5 см величины критической нагрузки и максимальной нагрузки составили соответственно: Р  0,2), которые будут оставаться стабильными, когда расчетные напряжения составляют 75% от σт.
0,2), которые будут оставаться стабильными, когда расчетные напряжения составляют 75% от σт. ;
;



