Результаты испытания детали на долговечность
Определим число циклов и время, необходимые для подрастания сквозной трещины от начального размера до критического, интегрируя полученную из эксперимента зависимость для скорости распространения трещины:
Результаты приведены в табл. 2, откуда следует, что долговечность рассматриваемой детали составляет 1106 суток (при длительности одного цикла нагружения равной одному часу) и что трещина удваивает свою длину (по отношению к начальной) за время, равное примерно одной трети долговечности. Поэтому имеет смысл назначить шестикратный запас по долговечности для осмотра конструкции и проводить дефектоскопический контроль два раза в год (1106:6=184 суток).
Пример 15. Обследование методами неразрушающего контроля позволило обнаружить в анкерном стержне экструзионного пресса поверхностную трещину глубиной
если Заводу необходимо чтобы пресс работал. На сколько же можно отложить замену стержня? Заводской инженер находится перед выбором: 1) через 24 месяца стержень все равно спишут, 2) через 14 месяцев пресс остановят, поскольку подойдет срок планового ремонта, 3) кратчайший срок, в который возможна поставка идентичного стержня, составляет 2,5 месяца, 4) кратчайший срок замены поврежденного стержня временным – около 2 недель, 5) работа пресса не безопасна, он должен быть остановлен до замены стержня. Переведем данные в систему СИ. Наибольшая нагрузка: 1850 тс = 18,1 МН, общая площадь сечений стержня: По таблице коэффициентов интенсивности напряжений (табл. 8) находим, что для поверхностной трещины Y = 1,88 для глубины Итак, уравнение роста трещины (11) принимает вид
или
Через 24 месяца, т.е. через 27. a. Экструдированный пруток из сплава 7075-Т6511, имеющий форму квадрата, со стороной 10 см и длину 20 см, обтачивают с целью, получения тонкостенного цилиндра, закрытого с одного конца, длиной 20 см и внешним диаметром 9 см. Цилиндр оснащен поршнем диаметром 7 см, предназначенным для повышения давления внутри цилиндра до 55 МПа. Случайная поломка в системе вызвала неожиданное повышение давления до неизвестной, величины, в результате чего цилиндр разрушился. Анализ поверхности разрушения позволил выявить дефект структуры, имеющий форму эллиптической несплошности (поры), длиной 0,45 см, расположеннойнаглубине 0,15 см от внутренней поверхности. Эта несплошность была ориентирована нормально по отношению к растягивающим напряжениям от центробежных сил цилиндра. Рассчитайте величину увеличения давления, приведшую к разрушению цилиндра. Данные по механическим свойствам приведены в табл.5 и 6 Приложений б. Пусть другой цилиндр имел аналогичным образом ориентированную несплошность, но имеющую полукруглую форму (а = 0,15 см). Сколько циклов увеличения давления выдержит цилиндр до разрушения? Допустим что цилиндр работает в нормальных условиях и материал подчиняется следующему соотношению, описывающему распространение усталостной трещины: da/dn = 5∙10-39(∆К)4, где da/dn и ∆К имеют размерности м/цикл и Па∙м1/2 соответственно.
28. В конструкции используется большая стальная плита. Радикально настроенный студент, вознамерившийся разрушить конструкцию, решил нанести очень острый надрез на краю плиты перпендикулярно направлению приложения напряжений. Если он будет удаляться от места совершения злодейского поступка со скоростью 5 км/ч, насколько далеко он уйдет, пока замышленное им воплотится в действительность? Ниже приведены дополнительные данные: а) плита подвергается воздействию циклического равномерного нагружения от 0 до 80 кН с частотой 25 Гц; б) стальная плита имеет ширину 20 см и толщину 0,3 см: в) предел текучести равен 1400 МПа, а вязкость разрушения в условиях плоскодеформированного состояния 48 МПа∙м1/2; г) нанесенный студентом надрез имел длину 1 см (в направлении по толщине); д) трещина распространялась со скоростью, пропорциональной квадрату размера зоны пластической деформации в области вершинытрещины; е) проведенный после разрушения фрактографический анализ выявил наличие усталостных - бороздок шириной 2,5
29. Если бы плита из предыдущей задачи имела толщину 0,15 или 0,6 см, смог бы злоумышленник уйти до того, как его план увенчался успехом (и на сколько дальше уйти)? Примите, что нагружение плиты осуществлялось таким образом, чтобы поддерживать напряжение постоянным.
30. Много лет назад в Биг Бене-колоколе, расположенном в здании Парламента в Лондоне, была обнаружена трещина. Для того чтобы избежать катастрофического разрушения и/или ее полного развития, было решено заменить язык колокола на меньший и повернуть колокол таким образом, чтобы изменить место удара языка. Используя концепции механики разрушения, объясните, как указанные мероприятия способствовали продлению жизни Биг Бена до наших дней. 31. а. Очень широкая плита, изготовленная из материала с вязкостью разрушения, определенной в условиях плоскодеформированного состояния, равной K1c = 55 МПа∙м1/2, содержит центральную трещину. Рассчитайте максимально допустимый размер дефекта, который может расти при циклическом нагружении, если σт = 1380 МПа, а расчетное напряжение составляет 50% от этой величины. Примите условия плоскодеформированного состояния. б. Сколько циклов нагружения от нуля до расчетного напряжения может выдержать плита, если общая длина начальной трещины составляет 2,5 мм? Примите, что скорости роста усталостной трещины изменялись в зависимости от коэффициента интенсивности напряжений, возведенного в четвертую степень. Коэффициент пропорциональности можно принять равным 1,1∙10-39.
32. Тонкостенный цилиндр из высокопрочного алюминиевого сплава (K1c = 24 МПа∙м1/2) имеет следующие размеры: длина 20 см, внешний диаметр 9 см, внутренний диаметр 7 см. Полукруглая трещина глубиной а = 0,25 см расположена с внутренней стороны и ориентирована вдоль линии, параллельной оси цилиндра. Сколько циклов приложения давления может выдержать цилиндр до разрушения? Давление внутри цилиндра достигает 75 МПа и распространение усталостной трещины в материале описывается выражением: da/dN =5∙10-39(∆К)4, где da/dN и ∆К имеют размерности м/цикл и Па∙м1/2 соответственно.
33. Стальная пластина (K1c = 54 МПа∙м1/2) содержит центральную трещину длиной 0,2 мм, ориентированную нормально по отношению к оси напряжений. На пластину воздействует чередующееся напряжение ∆σ=180 МПа при среднем напряжении 90 МПа. Лабораторными экспериментами было показано, что в указанных условиях в материале растет усталостная трещина, причем скорость роста da/dN изменяется в зависимости от ∆К в соответствии с соотношением: da/dN =4∙10-37(∆К)m, где da/dN и ∆К имеют размерности м/цикл и Па∙м1/2 соответственно. Величину m никогда не рассчитывали, однако было замечено, что скорость роста трещины изменяется прямо пропорционально квадрату размера зоны пластической деформации в области вершины трещины. Определите число циклов нагружения, которые пластина может выдержать до разрушения.
Расчет параметров надежности изделий
Пример 16. Пусть техническая система состоит из трех подсистем. Надежность каждой из них соответственно равна: Провести перераспределение норм надежности таким образом, чтобы произведение вероятностей трех подсистем соответствовало заданному требованию. Решение. Используя формулу (16):
получим:
Предположим, что мы произвольно задаем k = 1. Тогда, подставляя исходные данные в формулу (17):
получим:
Полученное значение надежности соответствует требуемому Ртр=0,65. Однако на основании полученного значения Р0тр можно заключить, что распределение средств, необходимых для повышения надежности, не было оптимальным. Другими словами, приложено больше средств для достижения заданного показателя, чем требовалось. Определим теперь k по формуле (18):
С этой целью вычислим три величины:
Так как
Это означает, что средства на повышение надежности необходимо распределить следующим образом: надежность подсистемы №1 увеличивают с 0,7 до 0,85; надежность подсистемы №2 — с 0,8 до 0,85; надежность подсистемы №3 оставляют на прежнем уровне. В результате вероятность безотказной работы всей системы Р = (0,85)
Пример 17. Техническая система предназначена для выполнения некоторой задачи. С целью обеспечения работоспособности система спроектирована со смешанным соединением элементов (рис. 6). Определить надежность системы, если известно, что надежность ее элементов равна:
Рис. 6. Структурная схема надежности техничеекой системы Решение. При расчете надежности воспользуемся формулами как для последователъного, так и для параллельного соединения элементов:
Пример 18. При проектировании подьемного механизма требуемая сила в гидроцилиндре должна соответствовать величине Решение. Подставляя исходные данные в формулу (19):
получим
По табл. 9 приложения находим искомую надежность (вероятность безотказной работы): Р
Пример 19. Требуется определить вероятность безотказной работы вала редуктора, изготовленного из стали 40Х, если известны следующие исходные данные: Решение. Определим условный запас прочности
Затем вычислим коэффициенты вариации:
По формуле (20):
вычислим квантиль
По табл. 9 приложения находим искомую вероятность безотказной работы вала редуктора: Р = 0,955.
Пример 20. В соответствии с техническим заданием разработана конструкторская документация на изделие типа подвижной установки. Выполнить расчет вероятности безотказной работы и коэффициента готовности, а также найти их среднее квадратические отклонения при следующих исходных данных: t = 6ч — время работы в течение суток (принимается пятидневная рабочая неделя); Для удобства используем сокращения: ц. — цикл; от. — отказ. Решение. По результатам анализа конструкторской документации установлено, что все элементы и узлы подвижной установки при выполнении ею работы функционируют в течение 6 ч в сутки. Составим структурную схему надежности изделия (рис. 7.). Для расчета надежности элементов 1-3 структурной схемы используем статистические данные, полученные при испытаниях, а расчет надежности элемента 4 проводим по справочным данным. Расчет надежности элемента 1. В соответствии с данными, полученными при эксплуатации металлоконструкций аналогичных изделий, предположим, что
определим
Рис. 7. Структурная схема надежности изделия.
Для вычисления коэффициента ремонта и его среднего квадратического отклонения используем соотношения:
2. Расчет надежности элемента 2. По результатам эксплуатации механических узлов аналогичных изделий имеем: Подставляя нсходные данные в известные формулы, получим:
3. Расчет надежности элемента 3. По результатам эксплуатации гидравлических узлов аналогичных изделий имеем: Подстановка исходных данных в известные формулы позволяет рассчитать:
Рис 8. Структурная схема надежности электроавтроматики. 4. Расчет надежности элемента 4. Структурная схема надежности электроавтоматики (рис. 8) представляет собой смешанное соединение элементов. Составим таблицу исходных данных интенсивностей отказов (табл. 3.). Для расчета надежности элемента 4 представим структурную схему в виде четырех ветвей А, В, С и D и определим надежность каждой ветви. Ветвь А.
где Таблица 3.
|

 , мм
, мм
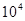 цикл
цикл

 ,
, измерен в
измерен в  .
. , наибольшее напряжение в стержнях:
, наибольшее напряжение в стержнях:  , наименьшее напряжение: 0, размах напряжений:
, наименьшее напряжение: 0, размах напряжений:  , начальная глубина трещины:
, начальная глубина трещины:  .
. . Для получения нижней оценки долговечности берем наибольшее значение Y = 1,88. Если трещина не полностью опоясывает сечения, то замена ее кольцевидной ведет, естественно, к консервативной оценке долговечности стержня.
. Для получения нижней оценки долговечности берем наибольшее значение Y = 1,88. Если трещина не полностью опоясывает сечения, то замена ее кольцевидной ведет, естественно, к консервативной оценке долговечности стержня.
 .
. циклов нагружения, глубина трещины будет равна
циклов нагружения, глубина трещины будет равна  , что превышает более чем вдвое диаметр стержня! Через 14 месяцев, т.е. через
, что превышает более чем вдвое диаметр стержня! Через 14 месяцев, т.е. через  циклов глубина трещины составит
циклов глубина трещины составит  . Значит, пресс можно спокойно эксплуатировать вплоть до планового ремонта, ведь критической глубиной является глубина
. Значит, пресс можно спокойно эксплуатировать вплоть до планового ремонта, ведь критической глубиной является глубина  .
. мм в области, где длина трещины достигала 2,5 см.
мм в области, где длина трещины достигала 2,5 см. = 0,7;
= 0,7;  = 0,8;
= 0,8;  = 0,9. Известно, что отказ любой одной подсистемы приводит к отказу системы в целом. Требуемое значение надежности системы равно Ртр = 0,65.
= 0,9. Известно, что отказ любой одной подсистемы приводит к отказу системы в целом. Требуемое значение надежности системы равно Ртр = 0,65. (16)
(16) = 0,7 0,8 0,9 = 0,504.
= 0,7 0,8 0,9 = 0,504. (17)
(17)

 (18)
(18) ;
; ;
; .
. , примем k = 2. В этом случае наибольшее значение индекса jсо свойством P>rравно двум. Далее, учитывая выражение (17), находим
, примем k = 2. В этом случае наибольшее значение индекса jсо свойством P>rравно двум. Далее, учитывая выражение (17), находим
 0,90 = 0,65.
0,90 = 0,65. = 0,95;
= 0,95;  = 0,9;
= 0,9;  = 0,9;
= 0,9;  = 0,8;
= 0,8;  =0,75;
=0,75;  =0,7.
=0,7.

 =2000±200 Н. Расчетный минимальный запас прочности в критическом сечении равен
=2000±200 Н. Расчетный минимальный запас прочности в критическом сечении равен  =2400±250 Н;
=2400±250 Н;  = 200 Н;
= 200 Н;  =250 Н. Определить надежность гидроцилиндра.
=250 Н. Определить надежность гидроцилиндра. (19)
(19)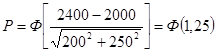
 0,895.
0,895.
 ;
; 
 (20)
(20)
 = 240 ч — время регламента (технического обслуживания), предусмотренное после каждого года эксплуатации (
= 240 ч — время регламента (технического обслуживания), предусмотренное после каждого года эксплуатации ( = 8760 ч).
= 8760 ч). =5000 ц.;
=5000 ц.;  =6 ч (длительность одного цикла работы) и
=6 ч (длительность одного цикла работы) и  =20 ч (среднее время восстановления одного отказа). Далее, подставляя исходные данные в формулы (21) и (22):
=20 ч (среднее время восстановления одного отказа). Далее, подставляя исходные данные в формулы (21) и (22): (21)
(21) при
при  (22)
(22) и
и  :
:





 = 4000 ц.;
= 4000 ц.;  = 10 ч.
= 10 ч.


 = 15 от.;
= 15 от.;  = 3000 ц.;
= 3000 ц.;  = 6 ч..
= 6 ч..





 — интенсивность отказов при работе;
— интенсивность отказов при работе;  — интенсивность отказов при хранении.
— интенсивность отказов при хранении.


