Задание 2. .

 

 

Построим диаграмму рассеивания экспериментальных данных:

· Выделим диапазон А1:В14, содержащие данные наблюдения;

· В меню Вставка выберем вид диаграммы: Точечная (в виде изолированных точек).

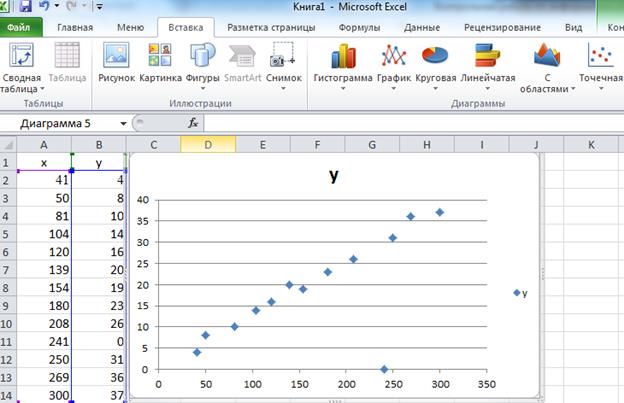
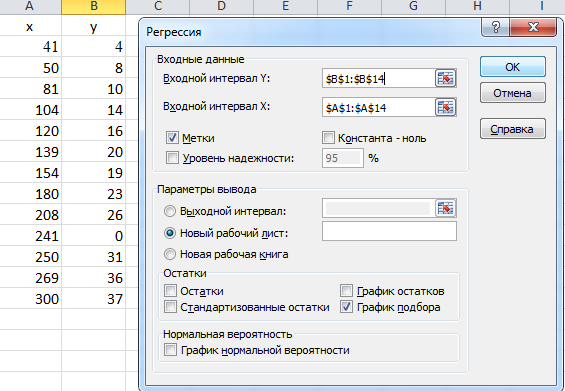
Рис. 4. Исходные данные и диаграмма рассеивания.

Линейное расположение точек и их сравнительно небольшой разброс относительно воображаемой прямой дают серьёзные основания для выбора линейной модели регрессии. Для более детального анализа возможности использования этой модели воспользуемся статистической процедурой Регрессия, входящей в Пакет анализа.

· В меню Данные выбираем Анализ данных – Регрессия – ОК. Откроется диалоговое окно Регрессия с пульсирующим курсором в поле ввода Входной интервал Y.

· Заполним поля (Рис. 5) и щёлкнем кнопку ОК.

Рис. 5

На вновь открывшемся рабочем листе появятся таблицы результатов реализации этой процедуры и График подбора.

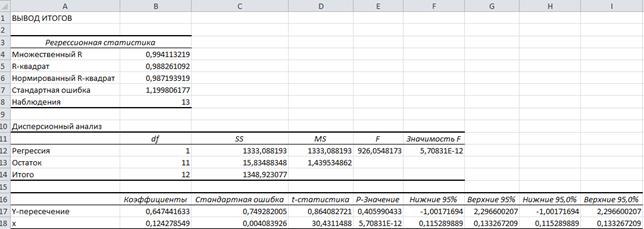
Рис. 6. Результаты анализа линейной модели регрессии

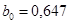Используя оценки и 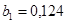(ячейки В17 и В18) параметров регресси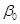и и 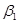, запишем выборочное уравнение парной линейной регрессии: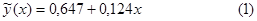

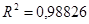Близкий к единице коэффициент детерминации (ячейка В5), очень большое расчётное значение статистики 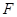(ячейка Е12) и ничтожно малая значимость 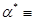Значимость свидетельствуют о высокой адекватности линейной модели (1). Это подтверждает и Х График подбора:

Рис. 7. Графическая иллюстрация результатов анализа модели регрессии

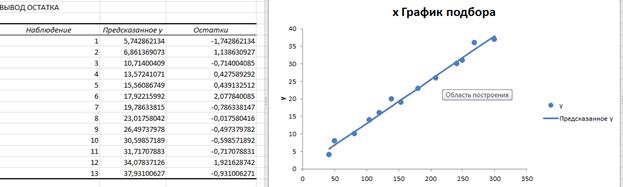
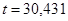Большое значение статистики 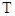(ячейка D18) и крайне малая Р-значимость 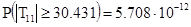(ячейка Е18) свидетельствует о том, что выборочный коэффициент регрессии 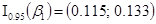существенно (значимо) отличается от нуля. Об этом же говорит и доверительный интервал для коэффициента регрессии 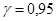(ячейки F18 и G18), соответствующий доверительной вероятности – нулевое значение коэффициента регрессии в этот интервал не попадает.

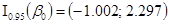Проверка значимости постоянной регрессии приводит к противоположному результату. Довольно большая значимость Р-значение (ячейка Е17) свидетельствует о том, что постоянная регрессии несущественно (незначимо) отличается от нуля. Это подтверждает и доверительный интервал для постоянной регрессии , соответствующий доверительной вероятности (ячейки F16:G16). Этот интервал накрывает нулевое значение постоянной .