Оценка параметров уравнения множественной регрессии
Параметры уравнения множественной регрессии оцениваются методом наименьших квадратов. Рассмотрим линейную зависимость: ytx=a+b1x1+b2x2+…+bpxp Возможны 2 подхода: Первый подход: строится система нормальных уравнений, решение которых позволяет получить оценки параметров регрессии. Для линейной зависимости имеем:
Её решение может быть осуществлено методом Крамера или определителей:
где
Частные определители получаются из Второй подход: На основе матрицы парных коэффициентов корреляции строится уравнение регрессии в стандартизованном масштабе.
Применяя метод наименьших квадратов к методу множественной регрессии в стандартизованном масштабе, после соответствующих преобразований получим сумму нормальных уравнений вида:
Решая систему методом определителей, находят стандартные коэффициенты регрессии - Стандартные коэффициенты регрессии показывают, на сколько среднеквадратических отклонений (сигм) изменяется в среднем результат, если соответствующий фактор хi изменяется на одну сигму при неизменном среднем уровне других факторов. Так как все переменные центрированы и нормированы, то стандартизованные коэффициенты регрессии сравнимы между собой. Сравнивая их между собой можно ранжировать факторы по силе их воздействия на результат. В парной зависимости стандартизованный коэффициент регрессии – это коэффициент корреляции – rxy. Во множественной регрессии коэффициенты «чистой» регрессии связаны со стандартизованными коэффициентами регрессии следующими формулами:
Параметр а определяется по следующей формуле: Рассмотрение стандартных коэффициентов регрессии позволяет их использовать при отсеве факторов из модели, то есть исключают факторы с наименьшим значением Рассматривая нелинейные зависимости но, приводимые к линейному виду, применяют метод наименьших квадратов, который используют не к исходной информации, а к преобразованным данным. Например, для степенной зависимости:
здесь переменные выражены в логарифмах, далее обработка метода наименьших квадратов та же: 1. строится сумма нормальных уравнений 2. определяются параметры lg a,b1, b2…bp 3. потенцируется значение lg a 4. записывают общий вид степенной функции Так как параметры степенной функции представляют собой коэффициенты эластичности, то они сравнимы по разным факторам. Для других зависимостей методика аналогична. Параметры более сложных моделей не имеют чёткой эконометрической интерпретации.
|



 …
…  ,
, - определитель системы,
- определитель системы, 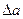 ,
,  …
…  - частные определители.
- частные определители.

 ,
,  …
…  - стандартизованные переменные, рассчитанные по формулам:
- стандартизованные переменные, рассчитанные по формулам: ,
,  , где
, где 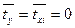 ,
,  .
.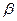 - стандартизованные коэффициенты регрессии.
- стандартизованные коэффициенты регрессии.
 .
.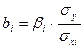 Это позволяет от уравнения регрессии в стандартном масштабе переходить к уравнению регрессии в натуральном масштабе.
Это позволяет от уравнения регрессии в стандартном масштабе переходить к уравнению регрессии в натуральном масштабе. .
.



