Частная корреляция.
Целесообразность внесения того или иного фактора в модель доказывается величиной показателя частной корреляции. Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влиянии других факторов, включённых в уравнение регрессии. Если рассматривается регрессия с р факторами, то возможны частные коэффициенты корреляции первого, второго и так далее р - первого порядка:
Сопоставление коэффициентов частной корреляции разного порядка по мере увеличении числа внешних факторов показывает процесс “очищения” зависимости результатного признака с наследственным фактором. Хотя частная корреляция разных порядков удобна при анализе, в практических исследованиях предпочтение отдают показателям частной корреляции самого высоко порядка, так как эти порядки являются дополнительными к уравнению множественной регрессии. Для линейной модели множественной регрессии
Данный коэффициент частной корреляции позволяет измерить тесноту связи между y и xi при неизменном уравнении других факторов. Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Коэффициенты парной корреляции называют коэффициентами нулевого порядка. Коэффициенты частной корреляции более высоких порядков можно определить через коэффициент частной корреляции более низких порядков по рекуррентной формуле.
Например, при двух факторах и i=1 данная формула имеет вид:
Для уравнения регрессии с тремя факторами частные коэффициенты корреляции второго порядка определяются на основе частных коэффициента корреляции первого порядка. Подсчитанные по рекуррентной формуле частные коэффициенты корреляции изменяются в пределах от –1 до +1. А по формуле через множественные коэффициенты детерминации от 0 до 1. В эконометрике частные коэффициенты корреляции не имеют самостоятельного значения. В основном их используют на стадии формирования модели в процедуре отсева факторов: строя многофакторную модель методом исключения переменных на первом шаге определяется уравнение регрессии с полным набором факторов и рассчитывается матрица частных коэффициентов корреляции. Далее выбирается фактор с наименьшей несущественной по t - критерию величиной частного коэффициента корреляции. Исключив данный фактор из модели, строится новое уравнение регрессии и процедура продолжается до тех пор, пока не окажется, что все частные коэффициенты корреляции существенно отличаются от нуля. Если исключён несущественный фактор, то множественные коэффициенты детерминации на двух смежных шагах построение регрессионной модели почти не отличаются друг от друга, то есть Зная частные коэффициенты корреляции можно определить совокупный коэффициент корреляции по формуле:
6. Оценка надежности результатов множественной регрессии и корреляции.
Значимость уравнения множественной регрессии в целом оценивается с помощью F критерия. Формула: Dфакт – факторная сумма квадратов на одну степень свободы. Dост – остаточная сумма квадратов на одну степень свободы. R2 – коэффициент (индекс) множественной детерминации. m – число параметров при переменных х. n – число наблюдений. Если факторное значение F - критерия превышает табличное, то уравнение статически значимо. Оценивают значимость не только уравнения в целом, но и фактора дополнительно включенного в регрессивную модель. Это связано с тем, что каждый фактор вошедший в модель может существенно увеличивать долю объяснённой вариации результатного признака. Кроме того, при наличии в модели нескольких факторов они могут ввозиться в модель в разной последовательности. Мерой для оценки включения фактора в модель служит частный F критерий Fxi. Он определяется по формуле:
Факторное значение частного F критерия сравнивается с табличным, при 5 % и 1 % уровне значимости и числе степеней свободы n-m-1 и 1. Если фактическое значение Fxi > Fтабл, то дополнительное включение фактора в модель статистически оправдано и коэффициент регрессии при xi - bi статистически значимо. Если факторное Fxi < Fтабл, то дополнительное включение фактора в модель xi не увеличивает долю объяснённой вариации y, следовательно, не целесообразно включать в модель xi. С помощью F критерия можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор xi вводится модель последним. Зная частный F критерий можно определить Т критерий. Стьюдента для коэффициента регрессии при i – м факторе.
Если t критерий для коэффициента чистой регрессии больше табличного, то подтверждается статическая зависимость включённых в модель факторов. Т критерий Стьюдента может быть рассчитан по формуле:
bi – коэффициенты чистой регрессии при факторе xi. mbi – средняя квадратическая ошибка коэффициента регрессии bi. Существует взаимосвязь между квадратом частного коэффициента корреляции и частным F критерием. 7. Фиктивные переменные во множественной регрессии.
Построение регрессионных моделей возможно, когда в качестве факторов рассматриваются экономические переменные, принимающие не только количественные значения на некотором интервале, но и факторы, имеющие 2 и более качественных уровня. Это могут быть разного рода атрибутивные признаки, например, профессия, образование, пол, принадлежность к региону, социальной группе, климатические условия. Чтобы ввести такие переменные в модель, им присваиваются цифровые метки, т.е. качественные переменные преобразуются в количественные. Таким образом сконструированные переменные называются фиктивными. Пример 1. Изучалась группа лиц мужского и женского полов. у – количество потребляемого продукта х – цена продукта Было построено уравнение: (1) Аналогичные уравнения могут быть построены отдельно для лиц мужского пола (2) и отдельно для лиц женского пола (3): (2) (3)
Предположим, что существуют различия в потреблении продукта между мужчинами и женщинами, т.е. (4)
Тогда из уравнения (4) для лиц мужского пола может быть получено равенство (5) (6) Т.е. надо построить такие уравнения, в которых содержится только одна фиктивная переменная: или Мужской пол Женский пол Т.е. различие в потреблении продукта выражается в различии свободных членов. Таким образом, если фиктивная переменная имеет 2 качественных уровня, то в модель вводят 1 фиктивную переменную. Если число градаций (качественных уровней) фиктивной переменной равно k, то в модель вводится (k-1) фиктивная переменная. Пример 2. у – цена двухкомнатной квартиры х – площадь квартиры Пусть z – тип дома: кирпичный, панельный, деревянный.
Было построено уравнение: Кирпичный дом: Панельный дом: Деревянный дом: В отдельных случаях необходимо ввести 2 и более группы фиктивных переменных, т.е. 2 и более качественных фактора, каждый из которых имеет несколько градаций, например, при изучении потребления некоторого товара при учете таких факторов, как цена, доход, цена на взаимозависимый товар и др. учитываются качественные факторы: национальный состав населения, где продается товар, климатические условия при продаже товара, образование населения. При построении таких моделей из каждой группы фиктивных переменных следует исключить по одной переменной. Бывают случаи, когда регрессия строится только на фиктивных факторах. Пример 3. у – средняя заработная плата работников предприятий промышленности. В исследовании участвовало k регионов. Была построена модель:
Иногда в качестве результативного показателя используется фиктивная переменная, например при обработке данных в социологическом опросе: у – ответ на вопрос.
Модели, в которых y – фиктивная переменная, называются вероятностными. Для значения переменной у ставят в соответствие вероятности p и (1-p). И для построения таких моделей используют законы теории вероятностей и комбинаторики. Среди моделей с фиктивными переменными наибольшее распространение получили модели, в которых зависимая переменная у рассматривается как функция от ряда экономических количественных факторов
|

 - при постоянном действии фактора
- при постоянном действии фактора  .
. - при постоянном действии факторов
- при постоянном действии факторов  .
. - при постоянном действии факторов
- при постоянном действии факторов  .
. коэффициент частной корреляции можно определить по формуле:
коэффициент частной корреляции можно определить по формуле: ,
, - множественный коэффициент детерминации всего комплекса p факторов с результатом.
- множественный коэффициент детерминации всего комплекса p факторов с результатом. - множественный коэффициент детерминации без введения в модель фактора
- множественный коэффициент детерминации без введения в модель фактора  .
. ;
;
 , где р – число факторов.
, где р – число факторов.









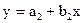
 , но сила влияния цены х на объем потребления у одинакова, т.е.
, но сила влияния цены х на объем потребления у одинакова, т.е.  . В этом случае необходимо построить общее уравнение регрессии с включением в него фактора «пол» в виде фиктивной переменной.
. В этом случае необходимо построить общее уравнение регрессии с включением в него фактора «пол» в виде фиктивной переменной.
 - фиктивные переменные, принимающие значения:
- фиктивные переменные, принимающие значения:

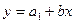 , а для лиц женского пола -
, а для лиц женского пола -  , т.е. можно увидеть различие в потреблении продукта:
, т.е. можно увидеть различие в потреблении продукта: 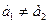 . Но уравнение (4) построить с помощью МНК нельзя, т.к. метод приведет к вырожденной матрице системы уравнений. Выходом из создаваемой ситуации является переход к уравнению вида (5) или (6):
. Но уравнение (4) построить с помощью МНК нельзя, т.к. метод приведет к вырожденной матрице системы уравнений. Выходом из создаваемой ситуации является переход к уравнению вида (5) или (6):

 , или
, или  . Например, если построено уравнение (5), то для лиц мужского пола будет верно равенство:
. Например, если построено уравнение (5), то для лиц мужского пола будет верно равенство:

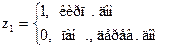










 с фиктивными переменными
с фиктивными переменными  . Такие модели отражают различие в формировании у по отдельным группам единиц совокупности.
. Такие модели отражают различие в формировании у по отдельным группам единиц совокупности.


