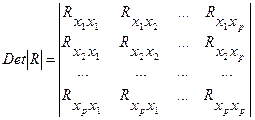Отбор факторов

Отбор факторов осуществляется в 2 стадии. На первой стадии подбираются факторы, исходя из сущности проблемы. На второй – на основе матрицы показателей корреляции определяют t-критерий для параметров регрессии.

Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1. они должны быть количественно измеримы (если необходимо включить качественный фактор, не имеющий количественного измерения, ему нужно придать количественную определённость)

2. факторы не должны быть коллинеарными (мультиколлинеарными) и не должны быть функционально зависимыми.

Факторы х₁ и х₂ являются коллинеарными (находятся в линейной зависимости), если R_x1x2>=0,7. Если факторы коллинеарные, то они дублируют друг друга и следовательно один из них следует исключить из регрессии. При этом предпочтение отдаётся не фактору более тесно связанному с результатом, а фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.

По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Большие трудности возникают при наличии мультиколлинеарноси факторов: когда более чем 2 фактора связаны между собой множественной зависимостью, то есть существует совокупное воздействие факторов друг на друга.

Включение в модель мультиколлениарных факторов нежелательно, так как приводит к следующим последствиям:

1. затрудняется интерпретация параметров множественной регрессии (теряется эконометрический смысл);

2. оценки параметров не надёжны, так как содержат стандартные ошибки и меняются с изменением наблюдений.

Для оценки мультиколлинеарности используют определитель матрицы парных коэффициентов корреляции между факторами:

Пример: для уравнения регрессии с 3 неизвестными y=a+b₁x₁+b₂x₂+c₃x₃+E, матрица коэффициентов корреляции имеет вид:

Если факторы x_i x_j (i≠j) неколлинеарны, то есть r_xixj=0, то Det|R|=1:

Если между факторами существует полная линейная зависимость, то есть парные коэффициенты корреляции между всеми парами факторов равны 1 r_xixj=1, то Det|R|=0:

Итак, чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлениарность факторов и ненадёжней результаты множественной регрессии. Наоборот, чем ближе к 1 определитель, тем меньше мультиколлениарность факторов.

Через коэффициенты множественной детерминации можно найти переменные, ответственные за мультиколлениарность факторов. Для этого в качестве зависимой переменной рассматривается каждый из факторов и рассматриваются следующие коэффициенты детерминации:

R²_x1|x2,x3… R²_x2|x1,x3… R²_x3|x1,x2…

Чем ближе значение коэффициента детерминации к 1, тем сильнее проявляется мультиколлениарность факторов. Сравнивая между собой коэффициенты множественной детерминации выделяют переменные, ответственные за мультиколлинеарность, оставляя факторы с минимальной величиной коэффициента множественной детерминации.

Отбор факторов, включаемых в регрессию – один из важнейших этапов использования регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные: