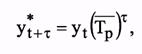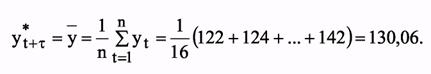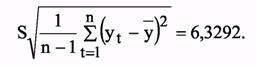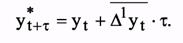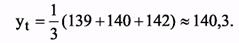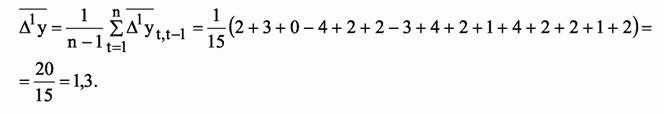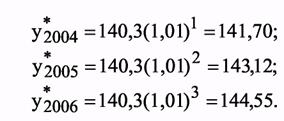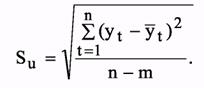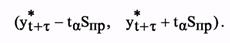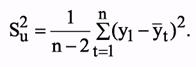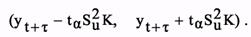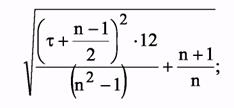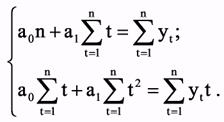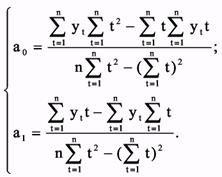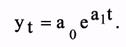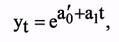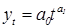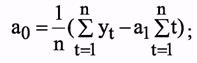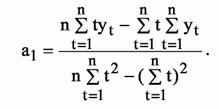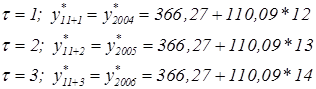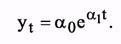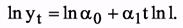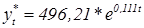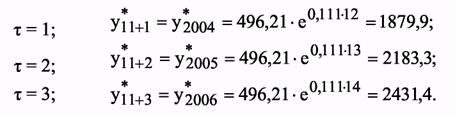ВВЕДЕНИЕ. 2. Организация предпринимательской деятельности
ВВЕДЕНИЕ При переходе к рыночной экономике приоритетными становятся вопросы подготовки специалистов, владеющих современными методами хозяйствования в условиях свободного предпринимательства и конкуренции. Перестройка производственных отношений в экономике, подвижность важнейших экономических нормативов (цен, тарифов, налоговых ставок), неустойчивость хозяйственных связей делают особо значимым учет долговременных аспектов развития производства. При этом в системе управления увеличивается число возможных управленческих решений, из которых необходимо выбрать оптимальное. Все эти факторы предопределяют повышение роли статистический методов, учета вероятностных факторов экономического и социального прогресса при составлении целевых программ развития структурных подразделений хозяйственного комплекса. Чем выше уровень использования методов экономико-статистических исследований, тем эффективнее планирование и управление экономическими процессами. Применение статистических методов обеспечивает активное целенаправленное участие специалистов на всех этапах принятия решений, что позволяет существенно повысить эффективность и качество управления. Каждый экономист должен иметь представление об основах прогнозирования с помощью методов математического моделирования и статистики.
Так как планом предусмотрено ограниченное число лекций, студенты-заочники осваивают курс самостоятельно. Поскольку курс тесно связан с практикой экономических отношений в условиях рынка, при освоении теоретического материала наряду с методической литературой необходимо изучить материалы, сопряженные с практикой социально-экономического прогнозирования, а также с опытом работы отдельных предприятий различных форм собственности.
ВЫПОЛНЕНИЮ 1. Назначение контрольной работы и требования по оформлению Цель контрольной работы: научиться решать конкретные практические задачи с применением методов экономико-статистических исследований. Номер варианта контрольной работы определяется в соответствии с последними цифрами зачетной книжки студента. Контрольная работа, выполненная не по своему варианту не засчитывается.
Прогнозирование социально-экономических процессов с использованием рядов динамик Используя динамический ряд, представленный таблицами вариантов, осуществить прогнозирование для периода упреждения 1) с использованием показателей средних характеристик: а) среднего уровня; б) среднего абсолютного прироста; в) среднего темпа роста; 2) по трендовой модели. Исходные данные для 10 вариантов рядов динамик представлены в следующих таблицах.
Одним из наиболее распространенных методов краткосрочного прогнозирования социально-экономических явлений и процессов является экстраполяция, т.е. распространение прошлых и настоящих закономерностей, связей, соотношений на будущее. Наиболее простым методом экстраполяции одномерных рядов динамики является использование средних характеристик: среднего уровня, среднего абсолютного прироста и среднего темпа роста. При использовании среднего уровня ряда динамики прогнозируемый уровень принимается равным среднему значению уровней ряда в прошлом:
Получается прогностическая точечная оценка, которая, вообще говоря, не совпадает с фактическими данными. Поэтому для средней указывается доверительный интервал прогноза
где ta - табличное значение t-критерия Стьюдента с n степенями свободы и уровнем доверия a; S среднеквадратичная ошибка средней:
Применение доверительного интервала для прогнозирования увеличивает степень надежности прогноза и позволяет учесть вариацию показателя вокруг средней в прошлом и будущем Прогнозное значение по среднему абсолютному приросту определяется по формуле
где у t - уровень ряда динамики, принятый за базу экстраполяции;
t - период упреждения. Если развитие ряда динамики описывается геометрической прогрессией или показательной кривой, то экстраполяция выполняется по среднему темпу роста. Прогнозируемый уровень ряда определяется по следующей формуле
где Тр - средний темп роста. В качестве базового уровня для экстраполяции берется последний уровень ряда, так как будущее развитие начинается именно с этого уровня. В некоторых случаях в качестве базового уровня лучше брать расчетный уровень, соответствующий тренду, описывающему динамический ряд. Для этого определяют экспоненциальную кривую и на ее основе находят базовый уровень. Для выбора базового уровня можно прибегнуть к усреднению нескольких последних уровней, т.е. вычислить экспоненциальную или геометрическую среднюю нескольких последних уровней. Для вычисления среднего темпа роста можно воспользоваться следующей формулой:
Доверительный интервал прогноза по среднему темпу роста может быть построен в случае, когда средний темп роста определяется по экспоненциальной функции. Указанные способы экстраполяции тренда динамического ряда являются весьма приближенными.
Пример 3. Выпуск цемента за период с 1988 по 2003 г. характеризуется динамическим рядом, представленным в виде табл. 6.
При экстраполяции на основе среднего уровня используется принцип, при котором прогнозируемый уровень принимается равным среднему значению уровней в прошлом:
Доверительный интервал для средней вычислим по формуле
Табличное значение t- статистики Стьюдента c 15 степенями свободы при уровне доверия a = 0,05; равно 2,13. Среднеквадратичное отклонение, связанное с колеблемостью выборочной средней и варьированием уровней ряда вокруг средней:
Подставив найденные значения в формулу, получим доверительный интервал (116,1639; 143,9561), который с доверительной вероятностью 0,95 включает прогнозируемое значение производства цемента в 2004 г. Считая, что общая тенденция производства цемента является линейной, прогноз производства цемента на 2004 г. вычислим по среднему абсолютному приросту:
За базу экстраполяции yt примем среднее арифметическое трех последних уровней исходного динамического ряда:
Средний абсолютный прирост:
Тогда прогнозное значение уровня на 2004, 2005, 2006 гг. 2004 =140,3 + 1,33 = 141,63 млн т; 2005 = 140,3 +1,33 * 2 = 142,96 млн т; 2006 =140,3 + 1,33*3 = 144,29 млн т. Экстраполяция по среднему темпу роста осуществляется по формуле
За базу экстраполяции примем среднее арифметическое трех последних уровней, т.е. 140,3. В этом случае прогнозируемый уровень ряда
Прогнозирование динамики социально-экономических явлений по трендовым моделям Прогнозирование с помощью трендов - также один из простейших и распространенных методов статистического прогнозирования. Суть этого метода заключается во временной экстраполяции. При этом предполагается следующее: период, для которого построен тренд, достаточен для выявления тенденций; анализируемый процесс устойчив и обладает инерционностью; не ожидается сильных внешних воздействий на изучаемый процесс, которые могут серьезно повлиять на тенденцию развития. При соблюдении этих условий экстраполяция осуществляется путем подстановки в уравнение тренда yt = f (t) значения независимой переменной t, соответствующей периоду упреждения t (прогноза). Получается точечная оценка прогнозируемого показателя (в конкретном году, квартале, месяце, дне) по уравнению, описывающему тенденцию. Полученный прогноз является средней оценкой для прогнозируемого интервала времени, так как тренд характеризует некоторый средний уровень на каждый момент времени. Отдельные наблюдения, как правило, отклонялись от него в прошлом. Естественно ожидать, что подобные отклонения будут происходить и в будущем. Поэтому определяется область, в которой с определенной вероятностью следует ожидать прогнозируемое значение, т.е. вычисляется доверительный интервал
где у t+t- точечный прогноз; ta - табличное значение t - критерия Стьюдента с n - m степенями свободы при уровне доверия а (здесь m - число параметров тренда); Su - средняя квадратичная ошибка тренда:
В основу расчета доверительного интервала прогноза положен показатель, определяющий амплитуду колебания ряда заданных значений признака. Чем больше амплитуда колебания, тем менее определено положение тренда и тем шире должен быть интервал для вариантов прогноза при одном и том же уровне доверия. В качестве такого показателя колеблемости ряда наблюдаемых значений признака обычно рассматривается среднеквадратичное отклонение фактических наблюдений от расчетных, полученных при выравнивании динамического ряда, т.е. средняя тренда. Доверительный интервал учитывает неопределенность, связанную с положением тренда. Но он должен учитывать также и возможность отклонения от тренда, т.е. среднеквадратичную ошибку прогноза. Тогда доверительный интервал прогноза имеет вид
Рассмотрим построение доверительного интервала, т.е. тех границ, в пределах которых будет находиться значение yt+t с заданной доверительной вероятностью для случая, когда тренд характеризуется прямой yt = а0 + a1t. Для того чтобы построить доверительный интервал необходимо прежде всего определить рассеяние уровней вокруг тренда. В качестве меры рассеяния принимается дисперсия Su, характеризующая отклонение фактических уровней от выровненных значений уt:
Стандартная ошибка прогноза:
Доверительный интервал имеет вид
где Su - среднее квадратичное отклонение фактических уровней динамического ряда от расчетных, называемое стандартной ошибкой тренда; К-величина, зависящая только от длины ряда и периода упреждения t:
ta - табличное значение t-критерия Стьюдента с n - 2 степенями свободы при уровне доверия а. С увеличением n значения К уменьшаются, а с увеличением t - увеличиваются. Поэтому достаточно надежный прогноз получается при относительно большом числе наблюдений (для линейного тренда n = 6, для параболического второй степени n = 13, для кубического n = 23), когда период упреждения не очень большой. При одном и том же n с ростом t доверительный интервал прогноза увеличивается.
Оценивание параметров тренда Параметры линейного тренда находятся методом наименьших квадратов из системы нормальных уравнений:
При решении системы получим расчетные формулы для определения параметров:
Метод наименьших квадратов и процедура построения тренда полностью переносятся и на случай, когда уравнение кривой может быть после некоторых преобразований сведено к линейному тренду: В практике криволинейного выравнивания широко распространены два вида преобразований: натуральный логарифм (ln) и обратное преобразование (1/t). При этом возможно преобразование как зависимой переменной уt, так и независимой t, или одновременно и той, и другой. Рассмотрим простую экспоненциальную кривую, ее уравнение и необходимые преобразования:
Это уравнение можно записать в другом виде:
От обеих частей уравнения возьмем натуральный логарифм. Получим
что можно решить с помощью стандартной процедуры, приведенной выше. Для некоторых кривых в табл. 7 приведены уравнения и необходимые преобразования.
Пример 4. Построение линейного тренда по динамике ежегодных затрат на строительство дорог (представлено в табл. 8).
yt=а0+а1t Параметры а0 и a1 вычисляются по формулам:
На основании табл. 8 и вышеуказанных формул находим:
Таким образом, трендовая модель имеет вид yt =366,27+110,09*t. Прогнозирование с помощью этой модели осуществляется весьма просто: необходимо вместо t в уравнение подставить нужное значение и найти прогноз. Определим прогноз для t = 1,2,3.
Пример 5. Построение трендовой модели для экспоненциальной кривой. Простая экспоненциальная кривая определяется уравнением
От обеих частей уравнения возьмем натуральный логарифм. Получим
с помощью стандартной процедуры (см. пример 4) находим:
Таким образом, трендовая модель имеет вид:
Осуществим прогнозирование для t = 1, 2, 3.
|
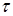= 1, 2, 3: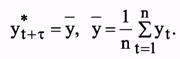
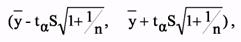
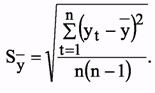
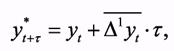
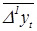- средний абсолютный прирост;
