УДК 621.3
Так же как и обратный применяется для замены вычитания сложением При этом: изображение положительной правильной двоичной дроби одинаково в прямом, обратном и дополнительном кодах. Для перевода отрицательной дроби: Необходимо нули заменить единицами, а 1 нулями. К младшему разряду прибавить единицу, затем слева от запятой поставить 1. Необходимо помнить: – Все цифры слагаемых, включая и цифры знаковых разрядов, расположенных слева от запятой участвуют в сложении как разряды единого числа – При переполнении, когда слева от запятой в результате сложения появляются две цифры, левая крайняя цифра отбрасывается, а оставшаяся цифра слева от запятой определяет знак результата – числа разрядов дробной части другого слагаемого, то перед тем как перевести отрицательную дробь в обратный код необходимо дополнить ее справа нулями до равенства разрядов второго слагаемого – если в результате сложения слева от запятой получился 1, то число отрицательное, если 0, то положительное (соответственно переводить ничего не нужно)
УДК 621.3
Методические указания к выполнению лабораторной работы «Анализ устойчивости электрической системы при малых возмущениях» по курсу «Электромеханические переходные процессы» для студентов специальностей 7.090603 и 7.090615 дневной и заочной форм обучения/ Составили: В.В.Нестерович, Т.К.Бараненко – Мариуполь, ПГТУ, 2002 г.
Кафедра электроснабжения промышленных предприятий
Утверждено на заседании кафедры "Электроснабжение промышленных предприятий". Протокол № ___ от ______________ г. Лабораторная работа № 1 Анализ устойчивости электрической системы при малых возмущениях 1. Объект исследования и цель работы Объектом исследования в настоящей лабораторной работе является простейшая электроэнергетическая система, состоящая из удаленной электрической станции, соединенной линией электропередачи с мощной приемной системой. Станция и система представлены на схеме (рис.1.1) эквивалентными генераторами G1 и G2. К шинам станции и приемной системы может быть подключена нагрузка (Н-1, Н-2, Н-3, Н-4). Линия электропередачи состоит из двух цепей (Л-1 и Л-2), коммутируемых выключателями Q1, Q2, Q3, Q4.
Рисунок 1.1 – Исследуемая система
Цель работы состоит в изучении методов определения угловых характеристик мощности простейшей электроэнергетической системы и вычисления предельных значений мощностей передающей станции системы с помощью практического критерия устойчивости. 2. Краткие сведения о методах расчета угловых характеристик мощности и вычисления предельных значений мощностей передающей станции В случае простейшей двухмашинной системы угловые характеристики активной и реактивной мощностей (
где
Предел передаваемой мощности для первого генератора в этом случае может быть определен как
Коэффициент запаса статической устойчивости равен
где 3. Подготовка к лабораторной работе Перед выполнением работы необходимо: 1) определить для заданного режима значения э.д.с. источников и величины соответствующих углов 2) построить угловую характеристику активной мощности, отдаваемой генератором в сеть; 3) определить для заданного режима величину коэффициента запаса статической устойчивости. Для определения э.д.с. источников, собственных и взаимных проводимостей ветвей следует предварительно составить схему замещения исследуемой сети. В схему замещения будут входить реактивные сопротивления всех элементов, включенных между генератором и шинами системы, сопротивление генератора, его э.д.с, а также сопротивление системы и ее э.д.с. Расчет рекомендуется вести с использованием точного приведения параметров элементов в относительных единицах. Величину базисной мощности следует принять равной полной номинальной мощности генератора G1. Базисное напряжение ступени, к которой подключен генератор, следует принять равным номинальному напряжению этого генератора. При исследовании статической устойчивости электрической системы с помощью практических критериев делается допущение о возможности представления синхронного генератора в виде неизменной э.д.с., приложенной за индуктивным сопротивлением. Значение этого сопротивления зависит от наличия и типа применяемого АРВ: - при отсутствии АРВ:
где
- при АРВ пропорционального типа:
где - при АРВ сильного действия:
Реактивное сопротивление двухобмоточного трансформатора может быть определено как
где
Реактивное сопротивление одной цепи воздушной или кабельной линии может быть найдено как
где
Реактивное сопротивление системы равно
где
Э.д.с. генератора может быть определено с использованием методики расчета напряжения в начале участка линии по данным ее конца
где
Будем считать, что ось отсчета совпадает с направлением вектора Напряжение в узле, к которому подключена нагрузка, равно
где Падение напряжения на данном участке сети в общем случае может быть найдено как
где
где Сопротивление нагрузки равно
где
Э.д.с. системы может быть определена как
где
где
Угол
где
Собственные и взаимные проводимости ветвей, входящие в выражение (1.1) могут быть найдены путем преобразования схемы или с использованием метода единичных токов.
4. Контрольные вопросы при собеседовании перед выполнением работы 1. Что такое угловая характеристика мощности? 2. Что такое собственные и взаимные сопротивления и проводимости ветвей? 3. Назовите способы определения собственных и взаимных проводимостей и сопротивлений. 4. Как определяются мощности через э.д.с., собственные и взаимные проводимости? 5. Что такое предельная передаваемая мощность и как она определяется? 6. Как определяется коэффициент запаса статической устойчивости? 5. Порядок выполнения работы Моделирование исследуемой системы следует вести с использованием пакетов расширения Simulink 4.0 и Power System Blockset, входящих в состав системы Matlab 6.0. Пакет расширения Simulink служит для имитационного моделирования динамических систем. Пакет Power System Blockset построен на основе пакета Simulink и предназначен для моделирования электротехнических систем. При построении модели следует использовать наряду с библиотеками элементов, входящих в состав этих пакетов, библиотеку libraryTr. Перечень блоков, которые рекомендуется использовать для моделирования элементов схемы, приведен в таблице 1.1. Таблица 1.1 – Блоки, используемые для моделирования элементов схемы
На рис. 1.2 приведен пример модели сети для одного из вариантов задания. Блок «Генератор» кроме выводов обмотки статора («А», «В» и «С») имеет выходы с сигналами равными значениям начальной фазы внутренней э.д.с. генератора («Е»), град., частоты вращения ротора («n»), об./мин., и активной мощности, отдаваемой генератором в сеть («Р»), о.е. При построении модели следует учесть, что трансформатор со схемой соединения обмоток «треугольник/звезда» создает сдвиг векторов напряжений первичной и вторичной обмоток равный 30 градусам. Так в модели, представленной на рис. 1.2, этот сдвиг компенсируется путем вычитания 30 градусов из измеренного значения при помощи блоков Constant («f0») и Sum. Блок Constant создает неизменный во времени сигнал, равный –30, а блок Sum суммирует этот сигнал с сигналом, поступающим от блока Генератор. Поскольку в любой модели, построенной с помощью блоков пакета Power System Blockset, должен присутствовать хотя бы один блок для измерения тока или напряжения, в состав модели, изображенной на рис. 1.2, включен блок Current Measurement («ia»), служащий для измерения тока генератора фазы А, и осциллограф Scope («Ia»).
Рисунок 1.2 – Пример модели сети для одного из вариантов задания
После создания модели необходимо зарисовать или распечатать для заданного значения мощности При моделировании рекомендуется установить параметры моделирования, соответствующие рис. 1.3.
Рисунок 1.3 – Окно ввода параметров моделирования Для различных значений мощности
Таблица 1.2
6. Указания по оформлению отчета Отчет по выполненной работе должен содержать: - формулировку цели работы, - исходную схему, - схему замещения, - результаты расчетов параметров схем замещения элементов, собственных и взаимных проводимостей, - полученные в результате расчета значения коэффициента запаса статической устойчивости, - графики, отображающие полученные путем расчета и моделирования угловые характеристики активной мощности - графики зависимостей - выводы. 7. Контрольные вопросы при защите работы 1. Чем можно объяснить несовпадение графика, полученного в результате моделирования, и графика, полученного расчетным путем? 2. Как повлияет на величину коэффициента статической устойчивости изменения способа регулирования возбуждения генератора? 3. Как повлияет на величину этого коэффициента изменение параметров отдельных элементов (мощности трансформатора, напряжения к.з. трансформатора, длины линии и т.п.)? 4. Как сказывается на изменении угловой характеристики мощности увеличение мощности подключенной нагрузки? 5. Поясните изменение характера графиков 6. Почему на графике, полученном в результате моделирования,
8. Варианты задания и справочные материалы Таблица 1.3
Продолжение табл. 1.3
Продолжение табл. 1.3
Продолжение табл. 1.3
9. Список рекомендуемой литературы 1. Веников В.А. Переходные электромеханические процессы в электрических системах.- М.: Высшая школа, 1985.- 536 с. 2. Перехідні процеси в системах електропостачання: Підручник для вузів. Вид. 2-е, доправ. та доп./ Г.Г. Півняк, В.М. Винославський, А.Я. Рибалко, Л.І. Несен/ За ред. Г.Г. Півняка.- Дніпропетровськ: Видавництво НГА України, 2000.- 597 с. 3. Переходные процессы в системах электроснабжения: Учебник/ В.Н.Винославский, Г.Г.Пивняк, Л.И.Несен и др.; Под ред. В.Н.Винославского.- К.:Вища шк., -1989.- 422 с. 4. Переходные процессы электрических систем в примерах и иллюстрациях/ Н.Д.Анисимова, В.А.Веников, В.В.Ежков и др.; Под ред. В.А.Веникова.- М.-Л.: Энергия, 1967.- 456 с. 5. Дьяконов В. Simulink 4. Специальный справочник.- СПб: Питер, 2002.-528 с.
|


 и
и  ), отдаваемых генератором G1 в сеть, могут быть получены с помощью выражений
), отдаваемых генератором G1 в сеть, могут быть получены с помощью выражений , (1.1)
, (1.1)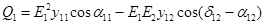 , (1.2)
, (1.2) и
и  - модули э.д.с. первого и второго генераторов;
- модули э.д.с. первого и второго генераторов; - модуль собственной проводимости ветви с генератором G1;
- модуль собственной проводимости ветви с генератором G1; - модуль взаимной проводимости ветвей, в которые включены генераторы G1 и G2;
- модуль взаимной проводимости ветвей, в которые включены генераторы G1 и G2; и
и  ;
; - угол между векторами
- угол между векторами  и
и 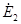 ;
; и
и  - активные и реактивные составляющие проводимостей
- активные и реактивные составляющие проводимостей  . (1.3)
. (1.3) , (1.4)
, (1.4) - активная мощность, отдаваемая первым генератором в систему при заданном режиме.
- активная мощность, отдаваемая первым генератором в систему при заданном режиме. ;
; , (1.5)
, (1.5) - сопротивление генератора, о.е.;
- сопротивление генератора, о.е.; - индуктивное сопротивление якоря генератора по продольной оси (приводится в справочниках в о.е. по отношению к номинальным параметрам генератора);
- индуктивное сопротивление якоря генератора по продольной оси (приводится в справочниках в о.е. по отношению к номинальным параметрам генератора); - базисная мощность, МВА;
- базисная мощность, МВА; - номинальная мощность генератора, МВА.
- номинальная мощность генератора, МВА. , (1.6)
, (1.6) - переходное индуктивное сопротивление генератора по продольной оси;
- переходное индуктивное сопротивление генератора по продольной оси; . (1.7)
. (1.7) , (1.8)
, (1.8) - напряжение к.з. трансформатора, %;
- напряжение к.з. трансформатора, %; - номинальная мощность трансформатора, МВА;
- номинальная мощность трансформатора, МВА; - номинальное напряжение обмотки трансфоматора, кВ;
- номинальное напряжение обмотки трансфоматора, кВ; - базисное напряжение той ступени, к которой подключена эта обмотка, кВ.
- базисное напряжение той ступени, к которой подключена эта обмотка, кВ. , (1.9)
, (1.9) - погонное реактивное сопротивление линии, Ом/км;
- погонное реактивное сопротивление линии, Ом/км; - длина линии, км;
- длина линии, км; , (1.10)
, (1.10) - мощность трехфазного к.з. на шинах системы, МВА;
- мощность трехфазного к.з. на шинах системы, МВА; - номинальное напряжение той ступени, к которой подключена система, кВ.
- номинальное напряжение той ступени, к которой подключена система, кВ. , (1.11)
, (1.11) - напряжение на шинах, которым подключен генератор, о.е.;
- напряжение на шинах, которым подключен генератор, о.е.; ,
,  - активная и реактивная мощности, проходящие через рассматриваемое сечение в исходном режиме, о.е.
- активная и реактивная мощности, проходящие через рассматриваемое сечение в исходном режиме, о.е. , т.е.
, т.е.  и
и  .
. , (1.12)
, (1.12) - падение напряжения на участке от э.д.с. генератора до данного узла.
- падение напряжения на участке от э.д.с. генератора до данного узла. , (1.13)
, (1.13) и
и  - величины являющиеся комплексно-сопряженными по отношению к величинам
- величины являющиеся комплексно-сопряженными по отношению к величинам  и
и  - мощность в начале участка между э.д.с. генератора и узлом, к которому подключена нагрузка;
- мощность в начале участка между э.д.с. генератора и узлом, к которому подключена нагрузка; - сопротивление этого участка (включающее и сопротивление генератора);
- сопротивление этого участка (включающее и сопротивление генератора); - потери реактивной мощности на внутреннем сопротивлении генератора, которые можно определить как
- потери реактивной мощности на внутреннем сопротивлении генератора, которые можно определить как , (1.14)
, (1.14) .
. , (1.15)
, (1.15) ,
,  - величины комплексно-сопряженные по отношению к величинам
- величины комплексно-сопряженные по отношению к величинам  и
и 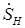 ;
; - мощность, потребляемая нагрузкой.
- мощность, потребляемая нагрузкой. , (1.16)
, (1.16) - падение напряжения на участке от узла, к которому подключена нагрузка, и э.д.с. системы, причем
- падение напряжения на участке от узла, к которому подключена нагрузка, и э.д.с. системы, причем и (1.17)
и (1.17) - мощность в начале участка между узлом, к которому подключена нагрузка, и э.д.с. системы;
- мощность в начале участка между узлом, к которому подключена нагрузка, и э.д.с. системы; - суммарное сопротивление этого участка (включающее и сопротивление системы);
- суммарное сопротивление этого участка (включающее и сопротивление системы); - потери реактивной мощности на сопротивлении первого участка (от э.д.с. генератора до места подключения нагрузки), которые можно определить как
- потери реактивной мощности на сопротивлении первого участка (от э.д.с. генератора до места подключения нагрузки), которые можно определить как . (1.18)
. (1.18)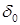 между векторами э.д.с. источников равен
между векторами э.д.с. источников равен , (1.19)
, (1.19) - соответственно, угол между вектором
- соответственно, угол между вектором  и этой осью.
и этой осью.
 , частоты вращения ротора генератора
, частоты вращения ротора генератора  , и угла между векторами э.д.с. генератора и системы
, и угла между векторами э.д.с. генератора и системы  от времени.
от времени.
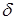 , которые будут использоваться для построения графиков зависимостей
, которые будут использоваться для построения графиков зависимостей  .
. 
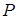 , о.е.
, о.е.
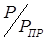
 .
. при
при  ?
? , МВА
, МВА
 , МВА
, МВА
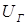 , кВ
, кВ
 , кВ
, кВ
 , МВт
, МВт



 , об/мин
, об/мин
 , МВА
, МВА
 , кВ
, кВ
 , кВ
, кВ
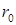 , Ом/км
, Ом/км



