Линейная функция
Рыночная ориентация портов. Внедрение маркетингового подхода к управлению производственно-экономической деятельностью портов. Опыт совместной деятельности Одесского порта и зарубежных стивидорных компаний. Идея портов третьего поколения возникла в силу того объективного факта, что в настоящее время морские порты становятся неотъемлемой частью международной транспортной системы и торговли. Одесский порт рассматривается как коммерческое предприятие и принимает непосредственное участие в международной конкуренции. Его деятельность обеспечиваются портовыми сообществами – т.е. формальными объединениями всех организаций и лиц, участвующих в осуществлении перевалочных операций и стивидорного сервиса, а так же пользователей портов. При этом лидирующую позицию занимает портовая администрация, которая представляет интересы правительства, а все другие участники портового сообщества, выполняя функции оператора, действуя на основе свободного предпринимательства, и следуют законам рынка. Ориентация на маркетинговый подход к управлению состоит в предоставлении продукции и услуг порта грузо- и судовладельцам – как конечным потребителям.
СЕНТЯБРЬ 2015 г.
Построение графиков линейной и квадратичной функций Вишняков А.Ю. Данная статья не содержит графических иллюстраций. Поэтому знакомиться с ее содержанием будет удобнее, имея под рукой лист бумаги и карандаш. Линейная функция
При изучении линейной функции Пример 1. Построить график функции Решение Составим таблицу значений функции.
Первая точка выбирается традиционно – точка пересечения прямой с осью ординат. А дальше обратим внимание, что разность значений функции - строим первую точку - переносим ее на 1 единицу вправо и две единицы вверх (это вторая точка, принадлежащая прямой): - вторую точку снова перемещаем на 1 единицу вправо и две единицы вверх и получаем третью точку искомой прямой; - далее все повторяется любое число раз. Пример 2. Построить график функции Решение Первая точка имеет координаты Рассмотрим теперь случай, когда угловой коэффициент линейной функции задается дробью. Пример 3. Построить график функции Решение Составим таблицу значений функции. Чтобы получить точки прямой с целочисленными координатами, возьмем значения х, кратные трем. Ну. а первая точка, по-прежнему, – точка пересечения прямой с осью ординат.
Построим точки на координатной плоскости. Видно, что каждая следующая точка получается из предыдущей сдвигом на 3 единицы вправо и 2 единицы вверх. Проводим прямую. Пример 4. Построить график функции Решение Первая точка имеет координаты Обратите внимание, что в случае дробного углового коэффициента линейной функции знаменатель дроби указывает количество единиц для перемещения точки вправо, а числитель – количество единиц, на которые переместится точка вверх (при
|

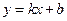 на уроках алгебры в 7-м классе учащиеся довольно успешно осваивают способ построения прямой по двум точкам. При этом составляется таблица, в которой задаются значения х и вычисляются соответствующие значения y. Однако при построении прямой часто допускаются неточности: из-за того, что выбранные точки очень близко расположены друг к другу, построенная прямая «уходит в сторону». Построить график линейной функции можно гораздо быстрее, если заметить определенные закономерности. Рассмотрим примеры.
на уроках алгебры в 7-м классе учащиеся довольно успешно осваивают способ построения прямой по двум точкам. При этом составляется таблица, в которой задаются значения х и вычисляются соответствующие значения y. Однако при построении прямой часто допускаются неточности: из-за того, что выбранные точки очень близко расположены друг к другу, построенная прямая «уходит в сторону». Построить график линейной функции можно гораздо быстрее, если заметить определенные закономерности. Рассмотрим примеры.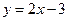 .
. , т.е. совпадает со значением углового коэффициента заданной функции. А значит, для построения точек на координатной плоскости вся информация заложена в коэффициентах заданной линейной функции. Алгоритм построения точек следующий:
, т.е. совпадает со значением углового коэффициента заданной функции. А значит, для построения точек на координатной плоскости вся информация заложена в коэффициентах заданной линейной функции. Алгоритм построения точек следующий: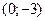 ;
; .
. . Каждая следующая получается из предыдущей смещением на 1 единицу вправо и на 3 единицы вниз.
. Каждая следующая получается из предыдущей смещением на 1 единицу вправо и на 3 единицы вниз. .
.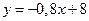 .
. . Заметим, что угловой коэффициент прямой
. Заметим, что угловой коэффициент прямой  . Значит, каждая следующая точка прямой будет получена из предыдущей смещением на 5 единиц вправо и на 4 единицы вниз. Строим точки и проводим прямую.
. Значит, каждая следующая точка прямой будет получена из предыдущей смещением на 5 единиц вправо и на 4 единицы вниз. Строим точки и проводим прямую.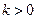 ) или вниз (при k<0).
) или вниз (при k<0).


