Квадратичная функция
2.1. С графиком квадратичной функции Записи таблицы можно избежать, если заметить одну закономерность в расположении указанных точек. Посмотрим таблицу значений функции
В третьей строке таблицы записана разность двух последующих значений функции. Видно, что полученные числа образуют последовательность нечетных чисел - первая точка – начало координат; - вторая точка получается из первой смещением на одну единицу вправо и на одну единицу вверх; - третья получается смещением второй точки на один вправо и три вверх; - четвертая точка получается переносом третьей на один вправо и пять вверх; - затем строятся точки левой ветви параболы за счет симметрии графика относительно оси ординат. Остается провести плавную линию через полученные точки, и парабола построена. 2.2. Перейдем теперь к квадратичной функции вида Пример 5. Построить график функции Решение Графиком функции служит парабола, ветви которой направлены вниз, а вершина находится в начале координат. Для построения других точек параболы вспомним про нечетные числа Пример 6. Построить график функции Решение Графиком функции – парабола, ветви которой направлены вверх. Вершина параболы находится в начале координат. Для построения других точек воспользуемся последовательностью
2.3. В 9-м классе учащиеся изучают квадратичную функцию 1) найти координаты вершины параболы 2) построить в системе координат полученную точку и провести оси вспомогательной системы координат (прямые 3) по коэффициенту а определить направление ветвей параболы; 4) построить во вспомогательной системе координат характеристические точки функции 5) провести плавную линию через указанные точки. График готов.
Пример 7. Построить график функции Решение Графиком функции – парабола. 1) Вычисляем координаты вершины параболы: 2) Строим точку координат (прямые проходят через указанную точку и параллельны осям ОХ и ОY). 3) Коэффициент при х2 в данной функции равен 1. Значит, для построения характеристических точек параболы применим ряд чисел 1,3,5,…., т.е. строим стандартную параболу, но во вспомогательной системе координат (пункт 2.1.). 4) Проводим плавную линию через полученные точки. Парабола построена.
|

 учащиеся знакомятся еще в седьмом классе. При этом для построения параболы, как правило, записывается таблица значений функции для
учащиеся знакомятся еще в седьмом классе. При этом для построения параболы, как правило, записывается таблица значений функции для  , затем полученные точки строят на координатной прямой и рисуют параболу. Более продвинутые ученики записывают таблицу только для
, затем полученные точки строят на координатной прямой и рисуют параболу. Более продвинутые ученики записывают таблицу только для  , строят полученные точки и проводят правую ветвь параболы. Затем, воспользовавшись симметрией графика относительно оси ординат, строят точки параболы для
, строят полученные точки и проводят правую ветвь параболы. Затем, воспользовавшись симметрией графика относительно оси ординат, строят точки параболы для  и рисуют вторую ветвь параболы.
и рисуют вторую ветвь параболы.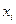





 (легко убедиться, что эта закономерность выполняется и далее, например,
(легко убедиться, что эта закономерность выполняется и далее, например,  ). Этот факт легко запоминается. А с учетом этой закономерности построить характеристические точки параболы можно так:
). Этот факт легко запоминается. А с учетом этой закономерности построить характеристические точки параболы можно так: , которая изучается уже в восьмом классе. Учащиеся узнают, что коэффициент а определяет направление ветвей параболы, а также растяжение или сжатие графика вдоль оси ординат. А для построения графика все равно просчитывают координаты точек. Но без этого можно обойтись, если знать указанную выше закономерность построения точек параболы
, которая изучается уже в восьмом классе. Учащиеся узнают, что коэффициент а определяет направление ветвей параболы, а также растяжение или сжатие графика вдоль оси ординат. А для построения графика все равно просчитывают координаты точек. Но без этого можно обойтись, если знать указанную выше закономерность построения точек параболы  , то для функции
, то для функции  .
. .
.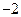 , получаем последовательность чисел
, получаем последовательность чисел 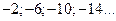 Знак
Знак  говорит о том, что смещение точек будет сделано вниз. На словах алгоритм построения звучит так: от начала координат одна единица вправо и две вниз; от новой точки одна единица вправо и шесть вниз; строим точки, симметричные полученным относительно оси ординат; проводим параболу.
говорит о том, что смещение точек будет сделано вниз. На словах алгоритм построения звучит так: от начала координат одна единица вправо и две вниз; от новой точки одна единица вправо и шесть вниз; строим точки, симметричные полученным относительно оси ординат; проводим параболу.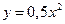 .
. получаем следующий порядок перемещений вдоль оси ординат
получаем следующий порядок перемещений вдоль оси ординат  . Строим точки на координатной плоскости: от точки
. Строим точки на координатной плоскости: от точки  1 клетка вправо и полклетки вверх, от полученной точки снова одна клетка вправо и полторы клетки вверх, потом от новой точки опять одна клетка вправо и две с половиной клетки вверх и т.д. (ясно, что в указанном случае за единичный отрезок на осях координат принимается одна клеточка в тетрадном листе). Затем строим точки левой ветви параболы за счет симметрии графика относительно оси OY и рисуем параболу.
1 клетка вправо и полклетки вверх, от полученной точки снова одна клетка вправо и полторы клетки вверх, потом от новой точки опять одна клетка вправо и две с половиной клетки вверх и т.д. (ясно, что в указанном случае за единичный отрезок на осях координат принимается одна клеточка в тетрадном листе). Затем строим точки левой ветви параболы за счет симметрии графика относительно оси OY и рисуем параболу. . Для построения ее графика с учетом выше сказанного можно применять следующий алгоритм:
. Для построения ее графика с учетом выше сказанного можно применять следующий алгоритм: ;
; и
и 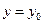 );
); .
. .
.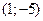 и проводим пунктиром вспомогательные оси
и проводим пунктиром вспомогательные оси


