Теоретические элементы для построения квантового компьютера.
1.Постулаты квантовой механики. П1.Состояние квантовой замкнутой системы задается единичным вектором в комплексном гильбертовом пространстве, образующем пространство состояний. Кубитам соответствует пространство состояний Сфера Блоха П2. Эволюция замкнутой квантовой системы описывается унитарным преобразованием П3. Измерение состояния Многокубитовые системы имеют состояние
Измерение в вычислительном базисе дают вероятность
П4.Пространство состояний составной системы является тензорным произведением пространства состояний её компонент. Пример: Двухкубитовое пространство состояний
2. Квантовый алгоритм — это алгоритм, предназначенный для выполнения на квантовом компьютере. Квантовый алгоритм представляет собой классический алгоритм, который задает последовательность унитарных операций (гейтов, или вентилей) с указанием, над какими именно кубитами их надо совершать. Квантовый алгоритм задается либо в виде словесного описания таких команд, либо с помощью их графической записи в виде системы вентилей (quantum gate array). Результат работы квантового алгоритма носит вероятностный характер[1]. За счёт небольшого увеличения количества операций в алгоритме можно сколь угодно приблизить вероятность получения правильного результата к единице. Множества задач, допускающих решение на квантовом компьютере и на классическом, совпадают. Квантовый компьютер, таким образом, не увеличивает число алгоритмически разрешимых задач. Весь смысл применения квантового компьютера в том, что некоторые задачи он способен решить существенно быстрее, чем любой из классических. Для этого квантовый алгоритм должен по ходу вычисления генерировать и использовать запутанные квантовые состояния. Любая задача, решаемая квантовым алгоритмом, может быть решена и классическим компьютером путем прямого вычисления унитарных матриц экспоненциальной размерности, получения явного вида квантовых состояний. В частности, проблемы, неразрешимые на классических компьютерах (например, проблема остановки), остаются неразрешимыми и на квантовых. Но такое прямое моделирование требует экспоненциального времени, и потому возникает возможность, используя квантовый параллелизм, ускорять на квантовом компьютере некоторые классические алгоритмы[2]. Ускорение на квантовом компьютере не связано с тактовой частотой процессора. Оно основано на квантовом параллелизме. Один шаг квантового вычисления совершает большую работу, чем один шаг классического. Не следует приравнивать квантовое вычисление к распараллеленному классическому. Например, квантовый компьютер не может решить задачу перебора быстрее, чем за Квантовое вычисление является процессом особого рода. Оно использует особый физический ресурс: квантовые запутанные состояния, что позволяет в некоторых случаях достигнуть поразительного выигрыша во времени. Такие случаи называются квантовым ускорением классических вычислений. Случаи квантового ускорения, на фоне общей массы классических алгоритмов, очень редки (см.[4]). Однако, это не умаляет принципиального значения квантовых вычислений, потому что они способны принципиально ускорить выполнение задач перебора.
3. Ква́нтовая суперпози́ция (когерентная суперпозиция) — это суперпозиция состояний, которые не могут быть реализованы одновременно с классической точки зрения, это суперпозиция альтернативных (взаимоисключающих) состояний. Принцип существования суперпозиций состояний обычно называется в контексте квантовой механики просто принципом суперпозиции. Если функции Из принципа суперпозиции также следует, что все уравнения на волновые функции (например, уравнение Шрёдингера) в квантовой механике должны быть линейными. Любая наблюдаемая величина (например, положение, импульс или энергия частицы) является собственным значением эрмитова линейного оператора, соответствующим конкретному собственному состоянию этого оператора, то есть определённой волновой функции, действие оператора на которую сводится к умножению на число — собственное значение. Линейная комбинация двух волновых функций — собственных состояний оператора также будет описывать реально существующее физическое состояние системы. Однако для такой системы наблюдаемая величина уже не будет иметь конкретного значения, и в результате измерения будет получено одно из двух значений с вероятностями, определяемыми квадратами коэффициентов (амплитуд), с которыми базисные функции входят в линейную комбинацию. (Разумеется, волновая функция системы может быть линейной комбинацией и более чем двух базисных состояний, вплоть до бесконечного их количества). Важными следствиями квантовой суперпозиции являются различные интерференционные эффекты, а для составных систем — зацепленные состояния. (Запутанные состояния).
4.Квантовый параллелизм — принцип, лежащий в основе работы квантовых компьютеров и позволяющий им потенциально превзойти в производительности классические компьютеры. В основе квантового параллелизма лежит использование при вычислениях суперпозиций базовых состояний, что позволяет одновременно производить большое количество вычислений с различными исходными данными. Например, 64-разрядный квантовый регистр может хранить до 5. Теорема о запрете клонирования — утверждение квантовой теории о невозможности создания идеальной копии произвольного неизвестного квантового состояния. Теорема была сформулирована Вуттерсом, Зуреком и Диэксом в 1982 году и имела огромное значение в области квантовых вычислений, квантовой теории информации и смежных областях. Состояние одной квантовой системы может быть сцепленным (запутанным) с состоянием другой системы. Например, создать сцепленное состояние двух кубитов можно с помощью однокубитного преобразования Адамара и двухкубитного квантового вентиля C-NOT. Результатом такой операции не будет клонирование, поскольку результирующее состояние нельзя описать на языке состояний подсистем (состояние является нефакторизуемым). Клонирование — это такая операция, в результате которой создается состояние, являющееся тензорным произведением идентичных состояний подсистем.
Теорема о запрете клонирования Доказательство Пусть мы хотим создать копию системы A, которая находится в состоянии
С составной системой можно произвести два различных действия. Мы можем измерить её состояние, что приведет к необратимому переходу системы в одно из собственных состояний измеряемой наблюдаемой и (частичной) потери информации об исходном состоянии системы A. Очевидно, такой сценарий нам не подходит. Другая возможность заключается в применении унитарного преобразования U, должным образом «настраивая» гамильтониан системы. Оператор U будет клонировать состояние системы, если
и для всех
то есть
Из этого следует, что либо Теорема о запрете клонирования доказана.
Неточное копирование. Хотя создание точных копий неизвестного квантового состояния невозможно, можно тиражировать его неточные копии. Для этого нужно привести исходную систему во взаимодействие с большей вспомогательной системой и провести специальное унитарное преобразование комбинированной системы, в результате которого несколько компонентов большей системы станут приблизительными копиями исходной. Такой процесс может быть использован для атаки на квантовые криптографические системы, а также для других целей в квантовых вычислениях.
Литература W.K. Wootters and W.H. Zurek, A Single Quantum Cannot be Cloned, Nature 299 (1982), pp. 802-803. D. Dieks, Communication by EPR devices, Physics Letters A, vol. 92(6) (1982), pp. 271-272. V. Buzek and M. Hillery, Quantum cloning, Physics World 14 (11) (2001), pp. 25-29. * V. Scarani, S. Iblisdir, N. Gisin, A. Acin: Quantum cloning, Reviews of Modern Physics. Vol.77. (2005) 1225–1256 (2005) arXiv.org:quant-ph/0511088 Бауместер Д., Экерт А., Цайлингер А. Физика квантовой информации. М.: Постмаркет, 2002. 376 с. Нильсен М., Чанг И. Квантовые вычисления и квантовая информация. М.: Мир, 2006. 824 с. Прескилл Дж. Квантовая информация и квантовые вычисления. Том 1. РХД, 2008. 464 с. ISBN 978-5-93972-651-1
Ква́нтовая запу́танность») — квантовомеханическое явление, при котором квантовые состояния двух или большего числа объектов оказываются взаимозависимыми. Такая взаимозависимость сохраняется, даже если эти объекты разнесены в пространстве за пределы любых известных взаимодействий, что находится в логическом противоречии с принципом локальности. Например, можно получить пару фотонов, находящихся в запутанном состоянии, и тогда если при измерении спина первой частицы спиральность оказывается положительной, то спиральность второй всегда оказывается отрицательной, и наоборот.
Копенгагенская интерпретация квантовой механики рассматривает волновую функцию до её измерения как находящуюся в суперпозиции состояний.
|

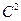 :
:  где
где  .
. .
. .
. в ортонормированном базисе
в ортонормированном базисе  дает результат j c вероятностью
дает результат j c вероятностью  . Измерение переводит систему из состояния
. Измерение переводит систему из состояния  .
.
 имеет состояния
имеет состояния
 , где
, где  — время работы детерминированного классического алгоритма перебора (см.[3]) Недетерминированный классический алгоритм решает её за время
— время работы детерминированного классического алгоритма перебора (см.[3]) Недетерминированный классический алгоритм решает её за время 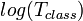 . Недетерминированный классический алгоритм требует экспоненциального ресурса памяти, то есть не является физически осуществимым, тогда как квантовый алгоритм не противоречит известным законам природы.
. Недетерминированный классический алгоритм требует экспоненциального ресурса памяти, то есть не является физически осуществимым, тогда как квантовый алгоритм не противоречит известным законам природы. и
и  являются допустимыми волновыми функциями, описывающими состояние квантовой системы, то их линейная суперпозиция,
являются допустимыми волновыми функциями, описывающими состояние квантовой системы, то их линейная суперпозиция,  , также описывает какое-то состояние данной системы. Если измерение какой-либо физической величины
, также описывает какое-то состояние данной системы. Если измерение какой-либо физической величины  в состоянии
в состоянии  приводит к определённому результату
приводит к определённому результату  , а в состоянии
, а в состоянии 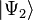 — к результату
— к результату  , то измерение в состоянии
, то измерение в состоянии 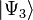 приведёт к результату
приведёт к результату  и
и  соответственно.
соответственно. значений одновременно, а квантовый компьютер может все эти значения одновременно обрабатывать. Тем не менее, извлечение результатов таких вычислений затруднено, что ограничивает область применения квантовых компьютеров[1].
значений одновременно, а квантовый компьютер может все эти значения одновременно обрабатывать. Тем не менее, извлечение результатов таких вычислений затруднено, что ограничивает область применения квантовых компьютеров[1]. . Для этого возьмем систему B с тем же самым гильбертовым пространством, находящуюся в начальном состоянии
. Для этого возьмем систему B с тем же самым гильбертовым пространством, находящуюся в начальном состоянии  . Начальное состояние, конечно, не должно зависеть от состояния
. Начальное состояние, конечно, не должно зависеть от состояния 

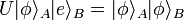
 и
и  .
.

 , либо состояния
, либо состояния 





