Получение запутанных квантовых состояний
Рис получение запутанных состояний. Лазерный луч падает на нелинейный кристалл. В результате спонтанного параметрического рассеяния (СПР) на выходе получаются два конуса поляризации H и V, несущие пары фотонов в запутанном квантовом состоянии (бифотоны)[34]
Генерация запутанных фотонов в результате спонтанного параметрического рассеяния *(СПР) лазерного потока в нелинейном кристалле. В простейшем случае источником S потоков запутанных фотонов служит определённый нелинейный материал, на который направляется лазерный поток определённой частоты и интенсивности (схема с одним эммитером)[33]. В результате спонтанного параметрического рассеяния (СПР) на выходе получаются два конуса поляризации H и V, несущие пары фотонов в запутанном квантовом состоянии (бифотоны)[34]. См рис Выбор конкретного материала зависит от задач эксперимента, используемой частоты и мощности[36]. В таблице ниже приводятся лишь некоторые часто используемые неорганические нелинейные кристаллы с регулярной доменной структурой (англ.)русск.[37] (РДС-кристаллы, англ. periodically poled):
Применение Всего через год после эксперимента Аспэ, в 1982 году, американский физик Ник Херберт предложил журналу «Foundations of Physics» статью с идеей своего «сверхсветового коммуникатора на основе нового типа квантовых измерений» FLASH (First Laser-Amplified Superluminal Hookup Статья была напечатана[41], и в результате развернувшейся дискуссии Вуттерсом, Зуреком и Диксом была сформулирована и доказана теорема о запрете клонирования. Теорема о запрете клонирования утверждает невозможность создания идеальной копии произвольного неизвестного квантового состояния. Квантовая коммуникация Теория квантовой механики запрещает передачу информации со сверхсветовой скоростью. Это объясняется принципиально вероятностным характером измерений и *теоремой о запрете клонирования. Представим разнесённых в пространстве наблюдателей А и Б, у которых имеется по экземпляру квантово-запутанных ящиков с котами Шрёдингера, находящимися в суперпозиции «жив-мёртв». Если в момент
Слабые квантовые измерения позволяют вовремя остановить «убийство» кота Шрёдингера и оставить его в исходной суперпозиции «жив-мёртв». Обход классических ограничений был найден[44] в 2006 году Коротковым и Джорданом из Калифорнийского университета за счёт слабых квантовых измерений (англ. weak quantum *measurement). Продолжая аналогию, оказалось, что можно не распахивать ящик, а лишь чуть-чуть приподнять его крышку и подсмотреть в щёлку. Если состояние кота неудовлетворительно, то крышку можно сразу захлопнуть и попробовать ещё раз. В 2008 году другая группа исследователей из Калифорнийского университета объявила[45] об успешной экспериментальной проверке данной теории. «Реинкарнация» кота Шрёдингера стала возможной. Наблюдатель А теперь может приоткрывать и закрывать крышку ящика, пока не убедится, что у наблюдателя Б кот окажется в нужном состоянии. Открытие возможности «обратного коллапса» во многом перевернуло представления о базовых принципах квантовой механики: Возникла идея не просто передачи потоков запутанных частиц в разнесённые в пространстве приёмники, но и хранения таких частиц неопределённо долгое время в приёмниках в состоянии суперпозиции для «последующего использования». Ещё из работ Раньяды 1990 года[46] было известно о таких расслоениях Хопфа, которые могли быть топологическими решениями уравнений Максвелла. В переводе на обычный язык это означало, что математически могут существовать ситуации, при которых пучок фотонов или отдельный фотон будет бесконечно циркулировать по сложной замкнутой траектории, выписывая тор в пространстве. До недавнего времени это оставалось просто ещё одной математической абстракцией. В 2008 году американские исследователи занялись анализом получаемых расслоений и их возможной физической реализацией. В результате[47] были найдены стабильные решения и технические способы, позволяющие реализовать такие решения. Оказалось, что пучок света действительно можно «свернуть в бублик» (точнее — в замкнутый тороидальный узел) и «положить на место», и такое состояние останется стабильным и самоподдерживающимся. На сентябрь 2011 об успешных лабораторных реализациях не сообщалось, но теперь это вопрос технических трудностей, а не физических ограничений. Помимо проблемы «складирования» запутанных частиц остаётся нерешённой проблема декогеренции, то есть утраты частицами запутанности со временем из-за взаимодействия с окружающей средой. Даже в физическом вакууме остаются так называемые виртуальные частицы. Несмотря на эпитет «виртуальный» в названии, они вполне успешно деформируют физические тела, как показывает эффект Казимира, следовательно, теоретически могут влиять на запутанные частицы. Декогере́нция — это процесс нарушения когерентности (от латинского cohaerentio — сцепление, связь), вызываемый взаимодействием квантовомеханической системы с окружающей средой посредством необратимого, с точки зрения термодинамики, процесса. Во время протекания этого процесса у самой системы появляются классические черты, которые соответствуют информации, имеющейся в окружающей среде. То есть система смешивается или запутывается с окружающей средой. Теория декогеренции имеет важное следствие: для макросостояния предсказания квантовой теории практически совпадают с предсказаниями классической теории. Декогеренция является одним из самых существенных технических препятствий на пути создания квантовых компьютеров. Для борьбы с декогеренцией разрабатываются, с одной стороны, различные методы изоляции квантовой сиcтемы, включая использование крайне низких температур и высокого вакуума, а с другой — введение в квантовые вычисления кодов, устойчивых к ошибкам, связанным с декогеренцией (обычно в таких схемах состояние логического кубита кодируется состоянием нескольких связанных физических кубитов). В настоящее время физики-экспериментаторы могут удерживать атомы или отдельно взятые фотоны в состоянии суперпозиции на протяжении значительных периодов времени при условии, что взаимодействие с окружающей средой сведено до минимума. Однако чем больше система, тем выше её подверженность внешним воздействиям. В крупных комплексных системах, состоящих из многих миллиардов атомов, декогеренция происходит почти мгновенно, и по этой причине кот Шрёдингера не может быть одновременно мертвым и живым на каком-либо поддающемся измерению отрезке времени.
Квантовая телепортация Квантовая телепортация), основанная на запутанных квантовых состояниях, используется в таких интенсивно исследуемых областях, как квантовые вычисления и квантовая криптография. Идея квантовых вычислений была впервые предложена Ю. И. Маниным в 1980 году[48]. На сентябрь 2011 года полномасштабный квантовый компьютер является пока гипотетическим устройством, построение которого связано со многими вопросами квантовой теории и с решением проблемы декогеренции. Ограниченные (в несколько кубитов) квантовые «миникомпьютеры» уже создаются в лабораториях. Первое удачное применение с полезным результатом продемонстрировано международным коллективом учёных в 2009 году. По квантовому алгоритму была определена энергия молекулы водорода[49]. Впрочем, некоторыми исследователями высказывается мнение, что для квантовых компьютеров запутанность является, наоборот, нежелательным побочным фактором[50]. Квантовая криптография используется для пересылки зашифрованных сообщений по двум каналам связи, квантовому и традиционному. Первый протокол квантового распределения ключа BB84 был предложен[51] Беннетом и Брассардом в 1984 году. С тех пор квантовая криптография являлась одним из бурно развивающихся прикладных направлений квантовой физики, и к 2011 году несколькими лабораториями и коммерческими фирмами были созданы работающие прототипы передатчиков и приёмников[52]. Следует отметить, что идея и привлекательность квантовой криптографии базируется не на какой-то повышенной или же «абсолютной» криптостойкости, а на гарантированном уведомлении, как только кто-либо попытается перехватить сообщение, его состояние меняется. Последнее же базируется на известных к началу разработок законах квантовой физики и в первую очередь на необратимости коллапса волновой функции[53]. В связи с открытием и успешным тестированием обратимых слабых квантовых измерений основы надёжности квантовой криптографии оказались под большим вопросом[54][55]. Возможно, квантовая криптография войдёт в историю, как система, для которой прототип «абсолютно надёжного» передатчика и прототип перехватчика сообщений были созданы почти одновременно и до начала практического использования самой системы.
Символ бифотона в статье на сайте Американского физического общества [58].
3 кубита квантового регистра против 3 битов обычного Ввведение Квантовый компьютер — вычислительное устройство, работающее на основе квантовой механики. Квантовый компьютер принципиально отличается от классических компьютеров, работающих на основе классической механики. Полноценный квантовый компьютер является пока гипотетическим устройством, сама возможность построения которого связана с серьёзным развитием квантовой теории в области многих частиц и сложных экспериментов; эта работа лежит на переднем крае современной физики. Первый разработанный высокоуровневый язык для такого вида компьютеров: Quipper[2]. Введение Идея о квантовых вычислениях была высказана Ю.И.Маниным в 1980 г.[3] Одна из первых моделей квантового компьютера была предложена[4] Ричардом Фейнманом в 1981 году. Вскоре П. Бениоф описал теоретические основы построения такого компьютера[5]. Необходимость в квантовом компьютере возникает тогда, когда мы пытаемся исследовать методами физики сложные многочастичные системы, подобные биологическим. Пространство квантовых состояний таких систем растет как экспонента от числа Квантовый компьютер использует для вычисления не обычные (классические) алгоритмы, а процессы квантовой природы, так называемые квантовые алгоритмы, использующие квантовомеханические эффекты, такие как квантовый параллелизм и квантовая запутанность. Если классический процессор в каждый момент может находиться ровно в одном из состояний обозначаемы кет-векторами:
Условие нормировки Базисные состояния могут иметь и более сложный вид. Квантовое состояние Унитарная квантовая операция (квантовый вентиль, quantum gate), в дальнейшем просто операция. Измерение (наблюдение). Если классические состояния Измерение есть случайная величина, принимающая значения Содержание понятия «квантовый параллелизм» в вычислении может быть раскрыто так: «Данные в процессе вычислений представляют собой квантовую информацию, которая по окончании процесса преобразуется в классическую путём измерения конечного состояния квантового регистра. Выигрыш в квантовых алгоритмах достигается за счёт того, что при применении одной квантовой операции большое число коэффициентов суперпозиции квантовых состояний, которые в виртуальной форме содержат классическую информацию, преобразуется одновременно»[7]. Кубиты Куби́т (q-бит, кьюбит, кубит; от quantum bit) — квантовый разряд или наименьший элемент для хранения информации в квантовом компьютере.
Как и бит, кубит допускает два собственных состояния, обозначаемых При любом измерении состояния кубита он случайно переходит в одно из своих собственных состояний. Вероятности перехода в эти состояния равны соответственно Кубиты могут быть связаны друг с другом, то есть на них может быть наложена ненаблюдаемая связь, выражающаяся в том, что при всяком изменении над одним из нескольких кубитов остальные меняются согласованно с ним. Иными словами, совокупность запутанных между собой кубитов может интерпретироваться как заполненный квантовый регистр. Как и отдельный кубит, квантовый регистр гораздо информативнее классического регистра битов. Он может не только находиться во всевозможных комбинациях составляющих его битов, но и реализовывать всевозможные тонкие зависимости между ними. Несмотря на то, что мы сами не можем непосредственно наблюдать состояние кубитов и квантовых регистров во всей полноте, между собой они могут обмениваться своим состоянием и могут его преобразовывать. Тогда есть возможность создать компьютер, способный к параллельным вычислениям на уровне своего физического устройства, и проблемой остаётся лишь прочитать конечный результат вычислений. Слово «qubit» ввел в употребление Бен Шумахер из Кеньон-колледжа (США) в 1995 г., а А. К. Звездин в своей статье предположил вариант перевода «q-бит»[1]. Иногда также можно встретить название «квантбит». Обобщением понятия кубит является кунит (Q-энк, куэнк; qudit), способный хранить в одном разряде более двух значений (например, кутрит. qutrit — 3, куквадрт — 4, …, куэнк — n)[2]. Идея квантовых вычислений состоит в том, что квантовая система из L двухуровневых квантовых элементов (квантовых битов, кубитов) имеет 2L линейно независимых состояний, а значит, вследствие принципа квантовой суперпозиции, пространство состояний такого квантового регистра является 2L-мерным гильбертовым пространством. Операция в квантовых вычислениях соответствует повороту вектора состояния регистра в этом пространстве. Таким образом, квантовое вычислительное устройство размером L кубит фактически задействует одновременно 2L классических состояний. Физическими системами, реализующими кубиты, могут быть любые объекты, имеющие два квантовых состояния: 1)поляризационные состояния фотонов, 2)электронные состояния изолированных атомов или ионов, 3)спиновые состояния ядер атомов, и т. д. Один классический бит может находиться в одном и только в одном из состояний
так что |a|² и |b|² — вероятности получить 0 или 1 соответственно при измерении этого состояния; Сразу после измерения кубит переходит в базовое квантовое состояние, соответствующее классическому результату. Пример: Имеется кубит в квантовом состоянии
В этом случае, вероятность получить при измерении
В данном случае, при измерении мы получили 0 с 64 % вероятностью. В результате измерения кубит переходит в новое квантовое состояние Приведем для объяснения два примера из квантовой механики: Фотон находится в состоянии Измерение раз и навсегда коллапсирует состояние фотона в одно из состояний Перейдем к системе из двух кубитов. Измерение каждого из них может дать 0 или 1. Поэтому у системы есть 4 классических состояния: 00, 01, 10 и 11. Аналогичные им базовые квантовые состояния:
Теперь |a|² — вероятность измерить 00 и т. д. Отметим, что полная вероятность |a|²+|b|²+|c|²+|d|²=1. Если мы измерим только первый кубит квантовой системы, находящейся в состоянии С вероятностью а второй — в состояние
С вероятностью а второй — в состояние
В первом случае измерение даст состояние
во втором — состояние
Мы снова видим, что результат такого измерения невозможно записать как вектор в гильбертовом пространстве состояний. Такое состояние, в котором участвует наше незнание о том, какой же результат получится на первом кубите, называют смешанным состоянием. В нашем случае такое смешанное состояние называют проекцией исходного состояния
где матрица плотности состояния В общем случае системы из L кубитов, у неё 2L классических состояний (00000…(L-нулей), …00001(L-цифр), …, 11111…(L-единиц)), каждое из которых может быть измерено с вероятностями 0—100 %. Таким образом, одна операция над группой кубитов затрагивает все значения, которые она может принимать, в отличие от классического бита. Это и обеспечивает беспрецедентный параллелизм вычислений.
Вычисление на квантовом компьютере Упрощённая схема вычисления на квантовом компьютере выглядит так: 1.берется система кубитов, на которой записывается начальное состояние. 2. Затем состояние системы или её подсистем изменяется посредством унитарных преобразований, выполняющих те или иные логические операции. 3.В конце измеряется значение, и это результат работы компьютера. Роль проводов классического компьютера играют кубиты, а роль логических блоков классического компьютера играют унитарные преобразования. Такая концепция квантового процессора и квантовых логических вентилей была предложена в 1989 году Дэвидом Дойчем. Также Дэвид Дойч в 1995 году нашёл универсальный логический блок, с помощью которого можно выполнять любые квантовые вычисления. Квантовый вентиль (квантовый логический элемент) — это базовый элемент квантового компьютера, преобразующий входные состояния кубитов на выходные по определённому закону. Отличается от обычных логических вентилей тем, что работает с кубитами, а следовательно подчиняется квантовой логике. Квантовые вентили в отличие от многих классических всегда являются обратимыми. Так как кубит можно представить вектором в двумерном пространстве, то действие вентиля можно описать унитарной матрицей, на которую умножается соответствующий вектор состояния входного кубита. Однокубитные вентили описываются матрицами размера 2 × 2, двухкубитные — 4 × 4, а n-кубитные — 2n × 2n.
Примеры квантовых вентилей Простейшие однокубитовые вентили: Тождественное преобразование:
Отрицание:
Фазовый сдвиг:
Преобразование Адамара:
Контролируемое U (C-U). Суть контролируемого U заключается в том, что на первый вход подаётся управляющий кубит, а на второй — управляемый. Если управляющий кубит равен единице, над управляемым проводится операция U, а если нулю — тождественное преобразование (кубит подается на выход без изменений). Если матрица U имеет вид
тогда матрица контролируемого преобразования C-U выглядит так:
Контролируемое отрицание (C-NOT). В этом случае
Также CNOT можно представить в виде таблицы истинности:
Рис. Графическое представление и таблица истинности для элементарного логического вентиля контролируемого НЕ. а –бит источника, b – бит цели. Каждая горизонтальная линия представляет собой состояние одного бита,изменяющегося слева нанправо. Символы на двух линиях, соединенные вертикальной чертой (не показана!) означают, совместное действие двух вентелей на эти биты. Таблица истинности контролируемого НЕ (обратимого XOR), соответствует таблице сложения двух битов, если в ней не учитывать бита переноса.
Первую физическую реализацию CNOT получили в 1995 году.[1] В этой реализации использовался один ион 9Be+, а два кубита были реализованы согласно схеме предложенной Cirac и Zoller на различных его состояниях (сверхтонкое расщепление ²S1/2для целевого кубита и 2 состояния гармонического осциллятора для управляющего кубита). Надежность работы элемента составила около 90 %.[2] Однокубитовое преобразование Адамара
Важными 3-х кубитными вентилями являются: Универсальный трехбитовый вентиль Тоффоли (Toffoli, часто CCNOT) используется для построения обратимой булевой логики. Его действие сводится к изменению сосотояния бита цели с, при условии, что оба неизменяемых бита источников Таблица истинности вентиля Тоффоли показана на рис.
Рис. Графическое представление и таблица истинности для трехбитового логического вентиля Тоффоли. а –бит источника, b –бит источника, c -бит цели. Состояние бита цели с меняется тогда и только тогда, когда оба неизменяемых бита источников (а,b) имеют значение 1. Каждая горизонтальная линия представляет собой состояние одного бита,изменяющегося слева направо. Символы на трех линиях, соединенные вертикальной чертой (не показана!) означают, совместное действие трех вентелей на эти биты.
вентиль Фредкина (англ. Fredkin gate, часто CSWAP) — также универсален. Если первый вход установлен, переставляет значения кубитов со входов 2 и 3. Иначе все три кубита остаются без изменений.
Универсальные квантовые вентили Набор квантовых вентилей называют универсальным, если любое унитарное преобразование можно аппроксимировать с любой заданной точностью конечной последовательностью вентилей из этого набора. Иными словами, универсальные квантовые вентили являются генераторами группы унитарных матриц. Можно доказать, что набор, состоящий из вентиля C-NOT и всех однокубитных вентилей, является универсальным. Возможны и другие универсальные наборы.
Пример реализации операции CNOT на зарядовых состояниях электрона в квантовых точках Один кубит можно представить в виде электрона в двухямном потенциале, так что Общий вид квантового состояния такого электрона:
где гамильтониан
для некоторой константы Вектор основного состояния
есть собственный вектор этого гамильтониана с собственным значением 0. Вектор первого возбужденного состояния
это собственный вектор этого гамильтониана со значением Никаких других собственных состояний (с определенным значением энергии) здесь нет, так как наша задача двумерная. Поскольку каждое состояние
То для реализации операции NOT перехода То есть гейт NOT дается просто естественной квантовой эволюцией нашего кубита при условии, что внешний потенциал задает двухямную структуру; это делается с помощью технологии квантовых точек. Для реализации CNOT надо расположить два кубита (то есть две пары ям) перпендикулярно друг другу, и в каждой из них расположить по отдельному электрону. Тогда константа Эта схема очень приблизительная и идеализирована; реальные схемы сложнее и их реализация представляет вызов экспериментальной физике.
В квантовом случае система из n кубитов находится в состоянии, являющимся суперпозицией всех базовых состояний, поэтому изменение системы касается всех 2n базовых состояний одновременно. Теоретически новая схема может работать намного (в экспоненциальное число раз) быстрее классической. Практически (квантовый) алгоритм Гровера поиска в базе данных показывает квадратичный прирост мощности против классических алгоритмов.
Алгоритмы Алгоритм Гровера позволяет найти решение уравнения Алгоритм Шора позволяет разложить натуральное число n на простые множители за полиномиальное от log(n) время. Алгоритм Залки — Визнера позволяет моделировать унитарную эволюцию квантовой системы Алгоритм Дойча — Джоза позволяет «за одно вычисление» определить, является ли функция двоичной переменной f(n) постоянной (f1(n) = 0, f2(n) = 1 независимо от n) или «сбалансированной» (f3(0) = 0, f3(1) = 1; f4(0) = 1, f4(1) = 0). Алгоритм Саймона решает проблему чёрного ящика экспоненциально быстрее, чем любой классический алгоритм, включая вероятностные алгоритмы. Было показано, что не для всякого алгоритма возможно «квантовое ускорение». Более того, возможность получения квантового ускорения для произвольного классического алгоритма является большой редкостью[8].
Квантовая телепортация Алгоритм телепортации реализует точный перенос состояния одного кубита (или системы) на другой. В простейшей схеме используются 3 кубита: телепортируемый кубит и запутанная пара, один кубит которой находится на другой стороне. Отметим, что в результате работы алгоритма первоначальное состояние источника разрушится — это пример действия общего принципа невозможности клонирования — невозможно создать точную копию квантового состояния, не разрушив оригинал. Не получится скопировать произвольное состояние, и телепортация — замена этой операции. Телепортация позволяет передавать квантовое состояние системы с помощью обычных классических каналов связи. Таким образом, можно, в частности, получить связанное состояние системы, состоящей из подсистем, удаленных на большое расстояние. Применение кван
|



 наблюдатель А открывает ящик, то его кот равновероятно оказывается либо живым, либо мёртвым. Если живым, то в момент
наблюдатель А открывает ящик, то его кот равновероятно оказывается либо живым, либо мёртвым. Если живым, то в момент  наблюдатель Б открывает свой ящик и находит там мёртвого кота. Проблема в том, что до исходного измерения нет возможности предсказать, у кого именно что окажется, а после один кот жив, другой мёртв, и назад ситуацию не повернуть.
наблюдатель Б открывает свой ящик и находит там мёртвого кота. Проблема в том, что до исходного измерения нет возможности предсказать, у кого именно что окажется, а после один кот жив, другой мёртв, и назад ситуацию не повернуть.


 составляющих их реальных частиц, что делает невозможным моделирование их поведения на классических компьютерах уже для
составляющих их реальных частиц, что делает невозможным моделирование их поведения на классических компьютерах уже для  . Поэтому Манин и Фейнман высказали идею построения квантового компьютера.
. Поэтому Манин и Фейнман высказали идею построения квантового компьютера. , то квантовый процессор в каждый момент находится одновременно во всех этих базисных состояниях, при этом в каждом состоянии
, то квантовый процессор в каждый момент находится одновременно во всех этих базисных состояниях, при этом в каждом состоянии  — со своей комплексной амплитудой
— со своей комплексной амплитудой  . Это квантовое состояние называется «квантовой суперпозицией» данных классических состояний и обозначается как
. Это квантовое состояние называется «квантовой суперпозицией» данных классических состояний и обозначается как
 .
. может изменяться во времени двумя принципиально различными путями:
может изменяться во времени двумя принципиально различными путями: , то унитарная операция есть решение уравнения Шредингера для этого потенциала.
, то унитарная операция есть решение уравнения Шредингера для этого потенциала. с вероятностями
с вероятностями  соответственно. В этом состоит квантовомеханическое правило Борна (англ.). Измерение есть единственная возможность получения информации о квантовом состоянии, так как значения
соответственно. В этом состоит квантовомеханическое правило Борна (англ.). Измерение есть единственная возможность получения информации о квантовом состоянии, так как значения  и
и  (обозначения Дирака), но при этом может находиться и в их суперпозиции, то есть в состоянии
(обозначения Дирака), но при этом может находиться и в их суперпозиции, то есть в состоянии  , где
, где 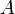 и
и  — комплексные числа, удовлетворяющие условию
— комплексные числа, удовлетворяющие условию  .
.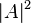 и
и 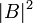 , то есть косвенно, по наблюдениям за множеством кубитов, мы всё-таки можем судить об исходном состоянии.
, то есть косвенно, по наблюдениям за множеством кубитов, мы всё-таки можем судить об исходном состоянии. , |a|² + |b|² = 1.
, |a|² + |b|² = 1.

 суперпозиции двух поляризаций. Это состояние есть вектор в двумерной плоскости, систему координат в которой можно представлять как две перпендикулярные оси, так что
суперпозиции двух поляризаций. Это состояние есть вектор в двумерной плоскости, систему координат в которой можно представлять как две перпендикулярные оси, так что  и
и 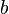 есть проекции кетвектора
есть проекции кетвектора 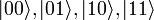 . И наконец, общее квантовое состояние системы имеет вид
. И наконец, общее квантовое состояние системы имеет вид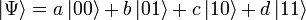 .
. первый кубит перейдет в состояние
первый кубит перейдет в состояние 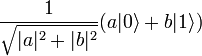
 первый кубит перейдет в состояние
первый кубит перейдет в состояние  .
. ,
,

 .
. ,
, ,
, ,
, .
. ,
,
 и матрица преобразования имеет вид:
и матрица преобразования имеет вид:

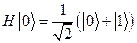
 .
. имеют значение 1. Может быть реализован на C-NOT и однокубитных вентилях. Похож по алгоритму работы на CNOT, но обращает значение последнего бита только, если два первых входа равны единице. В противном случае все входы подаются на выход неизменными.
имеют значение 1. Может быть реализован на C-NOT и однокубитных вентилях. Похож по алгоритму работы на CNOT, но обращает значение последнего бита только, если два первых входа равны единице. В противном случае все входы подаются на выход неизменными.
 . Зависимость его от времени есть зависимость от времени амплитуд
. Зависимость его от времени есть зависимость от времени амплитуд  ; она задается уравнением Шредингера вида
; она задается уравнением Шредингера вида
 имеет в силу одинакового вида ям и эрмитовости вид
имеет в силу одинакового вида ям и эрмитовости вид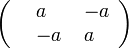


 .
. в состояние
в состояние ,
, и наооборот
и наооборот  достаточно подождать время
достаточно подождать время  .
. за время
за время  .
. кубит.
кубит.


