Башҡортостан Республикаһы Мәғариф министырлығы
2.
Нагрузка F, приложенная к ячейке, распределяется по четырем соседним узлам, примыкающим к этой ячейке в виде сил, равных F /4 = 550/4 = 137,5 кН.
Значения сил и их место приложения
3. По результатам расчета пластинки, построим ее упругую ось, эпюры изгибающих моментов Mx, My и скручивающих моментов Mxy в сечении I – I
Учитывая принцип независимости действия сил, и пользуясь данными таблицы П3, вычислим прогибы и моменты в расчетных точках сечения I – I, вызванные силами F = 550 кН. ;; ;
где - данные из таблицы П3.
В точке (x = 0,25 м, y = 4,75 м)
В точке (x = 1,75 м, y = 4,75 м)
В точке (x = 3,25 м, y = 4,75 м)
В точке (x = 4,75 м, y = 4,75 м)
В точке (x = 6,25 м, y = 4,75 м)
В точке (x = 7,75 м, y = 4,75 м)
В точке (x = 9,25 м, y = 4,75 м)
По эпюрам видно, что в сечении I-I наибольший прогиб W появляется в средней части пластинки и достигает 2,09 мм. Вблизи левого и правого краев наблюдается прогиб пластинки вверх, что указывает на возможный отрыв пластинки от основания. Большие изгибающие моменты Mx и My появляются в средней части пластинки, которые вызывают растяжение ее нижних слоев. Наибольшие крутящие моменты наблюдаются вблизи левого и правого краев пластинки, а в ее средней части он равен нулю. 4. К пластинке приложены четыре силы F = 550 кН в расчетных точках 2 – xF = 4,75 м, yF = 0,25 м; 5 – xF = 4,75 м, yF = 4,75 м; 7 – xF = 0,25 м, yF = 9,25 м; 9 – xF = 9,25 м, yF = 9,25 м; Вычислим изгибающие и крутящие моменты в этих точках от совместного действия всех четырех сил.
В точке 1 Mx = (140+1,92+0,24+0,24)×550/1000 = 78,32 кНм/м; My = (6,67-1,02+0,10+0,11)×550/1000 = 3,223 кНм/м; Mxy =(0,00+0,00+0,63-0,63)× 550/1000 = 0,00 кНм/м. В точке 2 Mx = (78,03-0,44-2,71-2,71)× 550/1000 = 39,69 кНм/м; My = (78,03-11,43-2,71-2,71)× 550/1000 = 33,65 кНм/м; Mxy =(0,00+0,00-0,10+0,10)× 550/1000 = 0,00 кНм/м. В точке 3 Mx = (9,16+0,11+0,66-0,07)× 550/1000 = 5,423 кНм/м; My = (9,16+0,16+0,66-0,17)× 550/1000 = 5,395 кНм/м; Mxy =(-70,58-0,13-1,01+0,17)× 550/1000 = -39,35 кНм/м. В точке 4 Mx = (9,17+0,11+0,66-0,07)× 550/1000 = 5,4285 кНм/м; My = (9,17+0,16+0,66-0,17)× 550/1000 = 5,4 кНм/м; Mxy =(70,57+0,13+1,01-0,17)× 550/1000 = 39,347 кНм/м.
Выберем точку 4 и проведем исследование в ней напряженно-деформированного состояния. Определим давление местной нагрузки на поверхность пластинки, принимая площадку приложения нагрузки квадратной со стороной равной 0,25 м.
Определим поперечные силы от местной нагрузки F . Найдем момент инерции сечения шириной в один метр.
Вычислим максимальные нормальные напряжения от изгибающих моментов, которые появляются в точке 2 Mx = 5,43 кНм и My = 5,4 кНм.
Вычислим касательные напряжения от крутящего момента в точке 4 Mxy =39,347 кНм
Определим максимальное нормальное напряжение от местной нагрузки p = 8,80 МПа sz = - p = - 8,80 МПа Вычислим максимальное касательное напряжение, вызванное поперечными силами Qzx и Qzy
Построим эпюры нормальных и касательных напряжений, вызванные внутренними силами в рассматриваемой расчетной точке 4
5. В окрестности выбранной точки 4 на верхней поверхности пластинки вырежем элементарный объем в форме кубика, покажем все напряжения, действующие на его площадках, и запишем тензор напряжений
Вычислим инварианты тензора напряжений:
Решим кубическое уравнение (7)
Сделаем подстановку .
Здесь новые коэффициенты равны:
Определим параметр, знак которого должен совпадать со знаком q:
Вычислим вспомогательный угол j
Корни промежуточного уравнения равны:
Проверим решение промежуточного уравнения
Вычислим значения главных напряжений
Расставим индексы главных напряжений в соответствии с условием .
Проверим полученные значения главных напряжений, вычислив по их значениям инварианты.
Определим положение главных площадок. Так как на верхней (нижней) площадке касательные напряжения отсутствуют, то эта площадка и нормальное напряжение Найдем положение главной площадки, на которой действует
и учтем, что n 1 = 0, получим
Отсюда имеем
Учитывая, что
Аналогично определим направляющие косинусы для площадки, где действует главное напряжение s2 = -2,07 МПа. l 2 = -0,707; m 2 =0,707; n 2 = 0. Проверим ортогональность (взаимно перпендикулярность) главных площадок.
Очевидно, что ортогональность соблюдается. 6. Используя теория прочности Губера-Мизеса-Генки, определим допускаемую нагрузку Fadm, из условия наступления предельного состояния в окрестности расчетной точки 2.
где s dan – опасное напряжение, соответствующее предельному состоянию материала, полученное при испытании на осевое растяжение s dan = s y = 20 МПа; s i – интенсивность напряжения
Вычислим допускаемую нагрузку:
F Башҡортостан Республикаһы Мәғариф министырлығы “Нефтекама педагогия колледжы”
|
; 
; 
; 
.
; 
; 
.
; 
; 
.
; 
;
; 
.
; 
; 
; 
.
; 
;
; 
.
; 
; 
; 
.
.
;
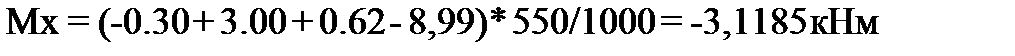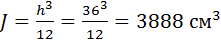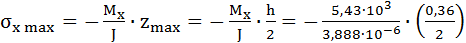= -0,251 МПА;
= -0,25 МПА;
= 1,82 МПА.
МПА.
, МПА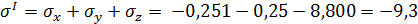
;
;
.
.
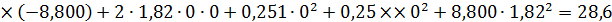и приведем уравнение к виду
;
;
;
.
.
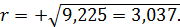
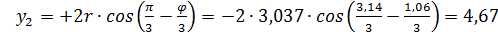, действующее на ней, являются главными. Следовательно,
Для этого воспользуемся первым уравнением системы (5), разделив его на m 1,
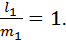
, найдем направляющие косинусы
.
;
;
.
Мпа.
.
