Критерий Коши для последовательностей.
Последовательность { xn } назовем последовательностью Коши или фундаментальной, если Теорема (Критерий Коши) Для того, чтобы последовательность { xn } сходилась, необходимо и достаточно чтобы она была фундаментальной.
Достаточность. Пусть {xn} - фундаментальная последовательность. Докажем, что она ограничена и Так как последовательность фундаментальна, то Предположим, A = max{ | x1 |, | x2 |, | x3 |,..., | xN − 1 |, | xn − ε |, | xn + ε | }. В отрезке [A, -A] содержатся все элементы последовательности, т.е. {xn} - ограниченна. В следствие теоремы Больцано-Вейерштрасса (
Эквивалентность определений предела функции по Гейне и по Коши.
Теорема о существовании корня непрерывной функции. Если функция
Ая теорема Вейерштрасса для непрерывных функций. Ая теорема Вейерштрасса для непрерывных функций. Теорема Кантора.
Теорема о производной композиции функций.
Теорема о производной обратной функции.
|


 Доказательство: Необходимость. Пусть {xn} сходится.
Доказательство: Необходимость. Пусть {xn} сходится. 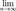


 .
. , в
, в  -окресности которой сущ-ют все элементы x1,x2,x3,...,xN − 1.
-окресности которой сущ-ют все элементы x1,x2,x3,...,xN − 1. ) < (xn − ε;xn + ε).
) < (xn − ε;xn + ε). в силу произвольности
в силу произвольности  .
. ,
, 


 непрерывна на отрезке
непрерывна на отрезке  и принимает на его концах значения разных знаков, то на этом отрезке существует по крайней мере один корень уравнения.
и принимает на его концах значения разных знаков, то на этом отрезке существует по крайней мере один корень уравнения.







