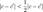Лемма о вложенных отрезках.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ГОСУДАРСТВЕННЫЙ ИНЖЕНЕРНО-ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ»
Факультет Логистики и транспорта Кафедра менеджмента организации
Самостоятельная работа №1 по дисциплине Общий Менеджмент: Построение диаграммы Исикавы (Вторая редакция)
Выполнил: Начкепия Георгий Гурамиевич
Студент 2 курса спец. 080506
Группы № 2201
Проверил: доцент Яковлева Наталия Васильевна Санкт - Петербург
Теорема о связи бесконечно малых и бесконечно больших последовательностей. Бесконечно малые и бесконечно большие последовательности тесно связаны между собой. Теорема. Последовательность { только тогда, когда последовательность Доказательство следует из того факта, что неравенство и определений бесконечно малых и бесконечно больших последовательностей. Лемма о вложенных отрезках. Для всякой системы вложенных отрезков
существует хотя бы одна точка c, принадлежащая всем отрезкам данной системы. Если, кроме того, длина отрезков системы стремится к нулю: Доказательство:1) Существование общей точки. Множество левых концов отрезков {an} лежит на числовой прямой левее множества правых концов отрезков {bn}, поскольку
Последнее неравенство означает, что c — общая точка всех отрезков данной системы. 2) Единственность общей точки. Пусть длина отрезков системы стремится к нулю. Покажем, что существует только одна точка, принадлежащая всем отрезкам системы. Предположим противное: пусть имеется две различные точки c и c', принадлежащие всем отрезкам системы:
Противоречие. Лемма доказана полностью.
|

 n },
n },  0 является бесконечно малой последовательностью тогда и
0 является бесконечно малой последовательностью тогда и является бесконечно большой.
является бесконечно большой. равносильно неравенству
равносильно неравенству 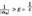

 то c — единственная общая точка всех отрезков данной системы.
то c — единственная общая точка всех отрезков данной системы. . В силу аксиомы непрерывности, существует точка c, разделяющая эти два множества, то есть
. В силу аксиомы непрерывности, существует точка c, разделяющая эти два множества, то есть в частности
в частности  .
. .Тогда для всех номеров n выполняются неравенства:
.Тогда для всех номеров n выполняются неравенства: 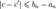 . В силу условия стремления к нулю длин отрезков для любого
. В силу условия стремления к нулю длин отрезков для любого для всех номеров n, начиная с некоторого будет выполняться неравенство: bn − an < E. Взяв в этом неравенстве
для всех номеров n, начиная с некоторого будет выполняться неравенство: bn − an < E. Взяв в этом неравенстве 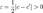 , получим
, получим