Непараметрические методы оценки вероятности статистических гипотез
В подразделе|подразделении| представлены методики расчета и анализа непараметрических критериев оценивания достоверности полученных результатов, рассмотрено понятие независимой и взаимоувязанной совокупности.
Вопросы для| изучения: —Как рассчитываются непараметрические критерии оценивания достоверности? —Когда возникает необходимость в применении определенных непараметрических критериев? —Как оценивается|оценивает| достоверность полученных критериев?
Цель: Ознакомить с понятием независимых и взаимосвязанных по| совокупности, научить адекватно подбирать определен непараметрический критерий для оценивания достоверности разницы|разности| результатов, проанализировать практическое| использование|употребление| непараметрических критериев.
Рассмотрены в предыдущих разделах статистические параметры (средняя арифметическая, среднее квадратичное отклонение, коэффициент вариации, средняя ошибка), которые используют для анализа вариационных рядов, являются его параметрами и требуют представления выходных данных в количественном виде. Однако при проведении медицинских исследований достаточно часто придется использовать методы статистического анализа данных, представленных в полуколичественном, полукачественном и качественном виде. Совокупность статистических методов, которые позволяют оценить их результаты как в количественном (числовом), так и в полуколичественном и качественном виде объединяют в группу непараметрических критериев оценивания.
Подавляющее большинство параметрических статистических методик предусматривают наличие нормального распределения|деления| вариант в исследуемой совокупности. Но на практике встречаются не только нормальные, но и другие виды раздела| признаков. При наличии таких ситуаций использование|употребление| параметрических критериев повышает вероятность ошибок|. Практическое|практичное| применение непараметрических критериев|, не связанное|повязал| с определенной формой распределения|деления| исследуемых признаков, делает целесообразным их самостоятельное использование|употребление| или в комплексе с параметрическими. Невзирая на|несмотря на| определенную простоту методик, надежность непараметрических критериев достаточно высока. Они могут быть использованы для оценивания достоверности медико-биологических результатов одной совокупности, разницы|разности|, двух и больше выборочных|избирательной| совокупностей. Критерий знаков и критерий Вилкоксона используют для оценки достоверности разницы двумя взаимосвязанными совокупностями.
Критерий знаков позволяет включать в анализ до 100 пар наблюдений и базируется на подсчете числа однонаправленных результатов при их парном сравнении. В таблице19 приведена динамика скорости оседания эритроцитов (СОЭ) за 10-тидневный период лечения. Основные этапы расчета по критериям знаков 1. Определение направленности разницы|разности| в сравнительных группах результатов. Динамика при этом обозначается соответствующими знаками: +, —, =. Из|с| дальнейшего| расчета исключают|выключают| результаты без динамики (=). 2. Подсчет|вычисление| числа наблюдений с позитивными|положительными| и негативными результатами. Из|с| 10 приведенных|наведенных| изменения|смена| оказались|проявляются| у 9 больных.
Таблица19. Динамика скорости оседания эритроцитов|эритроцита| (СОЭ)
3. Подсчет|вычисление| числа знаков, которые|какие| реже встречаются. Снижение СОЭ (-) обнаружено|выявляет| у 6 больных, а прирост (+) зарегистрирован в трех случаях. 4. Сравнение меньшего числа знаков (критерий Z) с табличными критическими значениями для соответствующего числа наблюдений. Для n = 9 определён критерий Z = 3 выше предельного табличного (Z0,05 = 2). Следовательно, нельзя сделать вывод о существенности динамики скорости оседания эритроцитов вероятности погрешности больше 5 % (р > 0,05).
Т-критерий Вилкоксона предусматривает возможность попарного сравнения от 6 до 25 пар наблюдений.
Методика анализа по Т-критерию| Вилкоксона приведена| в таблице 20.
1. Определяют разницу|разность| в парах|паре| наблюдения между конечным|концевым| и начальным|первоначальным| уровнями артериального давления. 2. Ранжирование полученных результатов за величиной разницы|разности| между показателями без учета направленности изменений|смены|. Результаты без динамики исключают из|с| последующего оценивания. Если два результата| имеют одинаковые абсолютные значения изменений|смены|, их ранги определяют как полгрусти порядковых|построчных| номеров. 3. Подсчет|вычисление| суммы однозначных рангов (позитивных|положительных| и негативных). 4. Оценивание за меньшей суммой рангов путем сравнения определенного Т-критерия| с табличным значением при соответствующем числе пар|пары| наблюдений.
Таблица 20. Уровень артериального давления у больных гипертонической болезнью до и после лечения (мм рт. ст.).
Критерий Вилкоксона Т=5 не превышает табличного значения для данного числа наблюдений - n=9|, Т о,о5 = 6. Следовательно, можно сделать вывод о существенности (статистическую значимость) динамики артериального давления у больных после лечения. Методика расчета критерия Колмогорова – Смирнова (
1. Числовые значения двух вариационных рядов объединяют в один вариационный ряд, варианты какого упорядочивают в порядке роста. 2. Определяют частоты вариант для обеих групп наблюдений|. 3. Определяют накопленные частоты для обеих групп. 4. Определяют накопленные частицы|долю|, для чего накопленные частоты делятся|делящийся| на число наблюдений для каждой группы. 5. Рассчитывается разница|разность| накопленных частиц|доли| групп X и У без учета знаков. 6. Определяют максимальную разницу|разность| — Д = 0,51. 7. Определяют критерий
8. Сравнивают полученный результат с предельным значением критерия Колмогорова-Смирнова|. Если Для данного задания
Таблица 21. Изменение радиоактивности крови подопытных животных, получавших (Х) и не получавших (У) лечение (в условных единицах).
При проведении статистического анализа иногда необходимо оценить достоверность разницы большей от двух количеству показателей клинико-статистических групп. В указанных ситуациях наиболее целесообразным является использование критерия соответствия — X2 (критерий Пирсона), который рассчитывается по формуле:
X2 =
где p - истинные частоты p1 - теоретические частоты В обобщенном виде практическое значение критерия соответствия X2 заключается в: • оценивании достоверности разницы|разности| между несколькими сравниваемыми группами при нескольких возможных результатах с разной|различной| степенью вероятности (например, три или четыре группы больных с разными|различными| методами лечения и их последствиями — разной|различной| частотою| осложнений|усложнения|); • определении наличия связи между двумя возбудителями (зависимость результатов лечения от возраста|века| больных, тяжести заболевания, связь между тяжестью патологии новорожденных и состоянием|станом| их физического развития); • оценивании идентичности распределения|деления| частот в двух и больше совокупности (аналогичность распределения|деления| больных по уровню клинических параметров при разных|различных| степенях тяжести патологии). На основе «нулевой» гипотезы определяют «ожидаемые|» результаты и сравнивают их с фактическими данными. Если разницы|разности| нет, можно сделать|совершить| вывод, что «нулевая» гипотеза подтвердилась. При наличии отличий фактических данных от теоретического раздела | определяют существенность разницы|разности| между сравниваемыми| группами.
Оценивание результатов (X2) проводится за специальной таблицей. Существенной считается разница в том случае, когда величина рассчитанного коэффициента превышает табличное значение при достоверности не ниже 95% (вероятность погрешности менее 5%-р<0,05).
Методику расчета коэффициента соответствия — X2 рассмотрим на примере оценивание влияния методов лечения на их результаты. 1. Приведем фактические результаты по трём методам| лечения (таблица 22).
Таблица 22. Результаты лечения больных по отдельным методикам
2. Рассчитываем «ожидаемые» результаты согласно «нулевой» гипотезе, основой|основанием| которой|какой| является доказательство, что разницы|разности| между результатами лечения за отдельными методиками нет. В этом случае за основу|основание| берем общее деление|разделение| больных, вылеченных всеми методами. Числовая характеристика «нулевой» гипотезы составляет: хорошие результаты в целом имели 54,5 %, удовлетворительные — 26,5 % | и неудовлетворительные — 19 % больных. В соответствии с|соответственно| указанным делением|разделением| определяют «ожидаемые» данные результатов лечения за отдельными методиками (значение определяем в целых числах) — таблица. 23. Таблица 23.
3. Сопоставляем фактические и теоретические данные (их разницу|) с расчетом величины отклонения и учетом| его направления (знака) — таблица. 24.
Таблица 24.
4. Рассчитываем квадрат отклонения теоретических данных от фактических и средний квадрат отклонения на одну «ожидаемую» группу. Данный этап расчета имеет такой вид в связи с тем, что на основе фактических отклонений невозможно определить его суммарную величину, поскольку она равняется нулю. При возведении отклонений в квадрат определяем их параметры для каждой группы (р — р1)2. Учитывая разное число больных в исследуемых группах величина отклонений может быть разной, потому квадрат их делимо на число соответствующих наблюдений каждой группы — (р — р1)2 / р1. Проведя расчеты, определяем (р — р1)2 и (р — р1)2 / р1. (таблица 25).
Таблица 25.
5. Определяем X2— итог результатов последнего этапа расчетов. В нашем случае X2= 19,5.
n1= (S-| 1) (г-| 1), где S — число групп больных (для нашего примера |приклада| - три). г — число результативных групп (три). |Число степеней свободы n1= (3 - 1) (3 - 1) = 4.
Полученный результат превышает табличное значение X2 для n1 = 4 по всем уровням достоверности. Следовательно, мы можем сделать вывод о существенности (достоверность) разницы между показателями при разных методах лечения — «нулевая» гипотеза не подтвердилась. Вопросы для контроля: • В каких случаях целесообразно использовать параметрические критерии? • Какие преимущества имеют непараметрические критерии? • Какие непараметрические критерии используют для оценивания достоверности разности |разносрезультатов исследования во взаимосвязанных совокупностей? • Какие непараметрические критерии используют для оценки достоверности разности|разность| результатов исследования в независимой совокупности?
|

 ) осуществляется в несколько этапов и рассмотрена в таблице21.
) осуществляется в несколько этапов и рассмотрена в таблице21.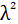

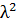 о,о5 = 1,84 и
о,о5 = 1,84 и 



